目录
一、实验目的
理解 RSA 算法原理:通过实现 RSA 算法,深入理解公钥加密、私钥解密以及密钥对生成的原理。掌握如何通过大数分解难题来保证数据安全。
实现加密与解密过程:通过编写 C 语言程序,实现 RSA 加密和解密的过程,了解如何使用公钥加密消息,使用私钥解密消息,验证加解密的正确性。
实现不同的填充机制:实现 RSAES-OAEP 和 RSAES-PKCS1-V1_5 两种常见的填充机制,理解它们如何增强 RSA 算法的安全性。
加密多次验证结果一致性:验证在相同密钥对的条件下,多次对同一明文进行加密时,加密结果是否相同,了解 RSA 算法中涉及的非确定性因素。
二、实验内容
使用C语言编译环境(VC++6.0)编程实现RSA算法。
三、实验原理
3.1 RSA 算法原理
RSA (Rivest–Shamir–Adleman) 是一种广泛使用的公钥加密算法,基于大整数分解的数学难题(即大数的质因数分解)来保证其安全性。RSA 主要用于数据加密和数字签名。
1. 密钥生成
RSA 密钥对包括公钥和私钥,用于加密和解密数据。生成密钥对的步骤如下:1.选择两个大素数 p 和 q,这两个数在数学上是保密的。
2.计算 n = p * q,这个 n 被用作公钥和私钥的一部分。
3.计算 φ(n) = (p-1) * (q-1),其中 φ(n) 是 n 的欧拉函数,用于后续的计算。
4.选择一个小于 φ(n) 且与 φ(n) 互质的整数 e,作为公钥的指数。通常选择较小的常数值(如 65537)。
5.计算 d,使得 d * e ≡ 1 (mod φ(n))。这里的 d 是 e 关于 φ(n) 的模反元素,即 d 是私钥的一部分。
所以,最终的公钥是 (e, n),私钥是 (d, n)。
2. 加密过程
加密过程的步骤是使用接收方的公钥 (e, n) 对消息进行加密。假设消息 M 是一个整数,且 M 必须满足 M < n,如果消息是文本,首先需要将其转换为数字。加密的过程如下:
将消息 M 转换为数字(通常使用 ASCII 编码)。
使用接收方的公钥 (e, n) 对消息进行加密:
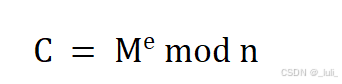
3. 解密过程
解密过程是使用私钥 (d, n) 对密文进行解密。解密的步骤如下:
使用接收方的私钥 (d, n) 对密文 C 进行解密:

4. RSA 算法的安全性
RSA 算法的安全性基于大数分解问题。即,对于一个给定的 n,很难从中推导出 p 和 q。一旦 n 的质因数分解被破解,私钥就会被揭露。
由于 RSA 的加密过程涉及对消息进行模幂运算,它在数学上是可逆的。只要公钥和私钥配对正确,加密后的数据就能通过私钥成功解密。
四、实验步骤
4.1 加解密算法设计
首先设计rsa加解密流程,之后在此基础上加入两种填充机制

4.2 加解密算法实现
4.2.1 素性检验
在本实验中,采取随机生成两个数字,再利用米勒罗宾算法判断其是否为素数的方式来生成两个大素数(本实验中其实是比较小的两个数字)。
米勒-拉宾素性测试的核心思想是通过“反复平方”和“模幂”运算来判断一个数是否是素数。如果一个数在经过若干次测试后仍然通过了测试,它很可能是素数,但也有一定的概率是合数。测试的次数越多,结果的可信度越高。
我们写出相应算法:
// 米勒-拉宾素性测试
int miller_rabin_test(int n, int k) {
// 若 n 是偶数,直接返回 false
if (n == 2) return 1;
if (n < 2 || n % 2 == 0) return 0;
// 计算 n-1 = 2^s * d,其中 d 为奇数
int d = n - 1;
int s = 0;
while (d % 2 == 0) {
d /= 2;
s++;
}
// k 次测试
for (int i = 0; i < k; i++) {
// 生成随机数 a,1 <= a <= n-1
int a = rand() % (n - 1) + 1;
int x = 1;
for (int j = 0; j < d; j++) {
x = (x * a) % n;
}
if (x == 1 || x == n - 1) continue; //基数 a 已经通过了这个测试,直接跳过本次循环,继续进行下一个测试
// 反复平方 a次,直到得到 n-1 或者 x == 1
int r = 0;
for (int j = 0; j < s - 1; j++) {
x = (x * x) % n;
if (x == n - 1) break;
if (x == 1) return 0; // 不是素数
}
if (x != n - 1) return 0; // 不是素数
}
return 1; // 是素数
}测试是否可行(计算100以内的所有素数以验证):

随机生成大数,如果通过素性测试,则将之定为pq中的一个,再用pq计算出n和phi

4.2.2 公私钥生成
首先计算私钥
随机生成一个数字e测试是否与phi互素,如果互素,则选定e
通过欧几里得算法判断是否互素
// 计算最大公约数(GCD)
int gcd(int e, int phi) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}如果结果是1,则e与phi互素,e通过测试
当得到e之后,我们通过扩展欧几里得计算出公钥d
// 求模反元素 (扩展欧几里得算法)
int mod_inverse(int e, int phi) {
int t = 0, new_t = 1;
int r = phi, new_r = e;
while (new_r != 0) {
int quotient = r / new_r;
int temp_t = t;
t = new_t;
new_t = temp_t - quotient * new_t;
int temp_r = r;
r = new_r;
new_r = temp_r - quotient * new_r;
}
if (t < 0) t += phi;
return t;
}由此我们得到公私钥e和d
4.2.3 模幂运算
此运算运用在加解密过程中

此运算中实际是将指数转化为二进制的形式,在运算过程中迭代

代码实现如下
// 快速模幂算法
long long mod_exp(long long base, long long exp, long long mod) {
long long result = 1;
base = base % mod;
while (exp > 0) {
if (exp % 2 == 1) {
result = (result * base) % mod;
}
exp = exp >> 1;
base = (base * base) % mod;
}
return result;
}至此,基本的加解密算法已实现,以下是两种不同的填充方式。
4.2.4 RSAES-OAEP 填充
OAEP 填充流程
假设消息长度 M 不超过 k−2h−2(h 是哈希长度,通常为 20 字节)。
RSA 模数长度为 k 字节
使用两个哈希函数 G 和 H,其输出长度为 h
填充步骤:
原始消息 M 加前置 0(零填充):
如果消息 M 长度不足 k−2h−2,先进行零填充,使其长度满足要求。
生成随机数 r:
随机生成长度为 h 字节的种子 r。
生成掩码数据:
使用哈希函数 G 生成掩码数据:
DataBlock=M | Padding | 0x01 | 0x00
MaskedDataBlock=DataBlock⊕G(r)
生成种子掩码:
使用哈希函数 H 生成种子掩码:
MaskedSeed=r⊕H(MaskedDataBlock)
拼接:
将填充数据组合成填充后的明文: PaddedMessage=MaskedSeed | MaskedDataBlock
代码实现如下:
// OAPE填充函数:填充至指定长度并生成One-hot编码
void oape_padding(char* s, int* padded_text, int max_len) {
int s_len = strlen(s);
for (int i = 0; i < s_len; i++) {
padded_text[i] = s[i]; // 填充原始文本
}
// One-hot编码填充字符
for (int i = s_len; i < max_len; i++) {
padded_text[i] = 0xFF; // 填充为0(表示填充位置),你也可以用其他标记
}
}
// 解填充函数:去除填充的One-hot编码
void oape_unpadding(char* decrypted, int* decrypted_text, int max_len) {
int i;
for (i = 0; i < max_len; i++) {
if (decrypted_text[i] == 0xFF) {
break; // 一旦遇到填充标记就停止
}
decrypted[i] = decrypted_text[i]; // 恢复原始字符
}
decrypted[i] = '\0'; // 添加字符串结束符
}4.2.5 RSAES-PKCS1-V1_5 填充
PKCS#1 v1.5 填充与解填充原理
PKCS#1 v1.5 填充标准广泛应用于 RSA 加密算法,旨在确保加密消息的长度与 RSA 模数相匹配。填充过程不仅保护了数据的安全性,还有助于防止某些加密攻击(如选择明文攻击)。
1. PKCS#1 v1.5 填充(pkcs1_v1_5_pad)
功能:将消息填充为特定格式,以适应 RSA 加密的要求。
填充格式:
消息必须填充到 RSA 模数的大小(k 字节),其中包括:
第一字节 0x00:填充开始标志。
第二字节 0x02:填充类型标志。
随机填充字节(不包含 0x00),确保填充后的数据满足 k - mLen - 1 字节的长度。
一个字节 0x00:填充结束标志。
剩余部分为原始消息数据。
填充步骤:
检查消息长度:如果消息的长度(mLen)超过了 k - 11(即填充后需要至少剩下 11 个字节),则报错并退出。这个 11 字节包括头部标志(0x00 0x02),填充数据和结束标志(0x00)。
填充开始:填充的第一个字节设置为 0x00,第二个字节设置为 0x02。
随机填充:接下来,为填充部分分配随机字节,直到填充数据的长度为 k - mLen - 3(为剩下的字节留出空间)。填充数据不能包含 0x00,因为这会干扰解填充过程。
结束标志:填充数据的最后一个字节设置为 0x00,然后将原始消息数据复制到填充后的消息末尾。
代码实现如下:
// PKCS#1 v1.5 填充
void pkcs1_v1_5_pad(unsigned char* message, size_t mLen, unsigned char* padded, size_t k) {
if (mLen > k - 11) {
fprintf(stderr, "消息太长,无法填充\n");
exit(EXIT_FAILURE);
}
padded[0] = 0x00;
padded[1] = 0x02;
for (size_t i = 2; i < k - mLen - 1; i++) {
do { padded[i] = rand() % 256; } while (padded[i] == 0);
}
padded[k - mLen - 1] = 0x00;
memcpy(&padded[k - mLen], message, mLen);
}
// PKCS#1 v1.5 解填充
void pkcs1_v1_5_unpad(unsigned char* padded, size_t k, unsigned char* message, size_t* mLen) {
if (padded[0] != 0x00 || padded[1] != 0x02) {
fprintf(stderr, "解填充失败,格式错误\n");
exit(EXIT_FAILURE);
}
size_t start = 2;
while (start < k && padded[start] != 0x00) start++;
if (start == k) {
fprintf(stderr, "解填充失败,未找到结束标志\n");
exit(EXIT_FAILURE);
}
*mLen = k - start - 1;
memcpy(message, &padded[start + 1], *mLen);
}五、实验结果
5.1 RAS无填充机制加解密
案例1第一次:输入Hello world! I am XuXuan!
生成参数如下:
生成的素数 p = 967, q = 809
生成的公钥指数 e = 14827
生成的公钥: (e = 14827, n = 782303)
生成的私钥: (d = 714883, n = 782303)

案例1第二次:输入Hello world! I am XuXuan!
生成参数如下:
生成的素数 p = 701, q = 877
生成的公钥指数 e = 9983
生成的公钥: (e = 9983, n = 614777)
生成的私钥: (d = 488447, n = 614777)

案例1第三次:输入Hello world! I am XuXuan!
生成参数如下:
生成的素数 p = 739, q = 293
生成的公钥指数 e = 11675
生成的公钥: (e = 11675, n = 216527)
生成的私钥: (d = 28499, n = 216527)

案例2:输入QQQQ11112222WWWW
生成参数如下:
生成的素数 p = 971, q = 349
生成的公钥指数 e = 28981
生成的公钥: (e = 28981, n = 338879)
生成的私钥: (d = 264541, n = 338879)

案例3:输入RAS未填充版本测试3
生成参数如下:
生成的素数 p = 317, q = 787
生成的公钥指数 e = 26761
生成的公钥: (e = 26761, n = 249479)
生成的私钥: (d = 33097, n = 249479)

5.2 RSAES-OAEP 填充机制加解密
案例1第一次:输入Hello world! I am XuXuan!
生成参数如下:
生成的素数 p = 7, q = 467
生成的公钥指数 e = 1909
生成的公钥: (e = 1909, n = 3269)
生成的私钥: (d = 145, n = 3269)

案例1第二次:输入Hello world! I am XuXuan!
生成参数如下:
生成的素数 p = 269, q = 421
生成的公钥指数 e = 20081
生成的公钥: (e = 20081, n = 113249)
生成的私钥: (d = 41681, n = 113249)

案例1第三次:输入Hello world! I am XuXuan!
生成参数如下:
生成的素数 p = 523, q = 359
生成的公钥指数 e = 17761
生成的公钥: (e = 17761, n = 187757)
生成的私钥: (d = 173545, n = 187757)

案例2:输入QQQQ11112222WWWW
生成参数如下:
生成的素数 p = 701, q = 613
生成的公钥指数 e = 18953
生成的公钥: (e = 18953, n = 429713)
生成的私钥: (d = 23417, n = 429713)

案例3:输入RSAES-OAEP 填充机制测试3
生成参数如下:
生成的素数 p = 13, q = 1013
生成的公钥指数 e = 11459
生成的公钥: (e = 11459, n = 13169)
生成的私钥: (d = 9467, n = 13169)

5.3 RSAES-PKCS1-V1_5 填充机制加解密
案例1第一次:输入Hello world! I am XuXuan!
生成参数如下:
生成的素数 p = 421, q = 23
生成的公钥指数 e = 8341
公钥: (e = 8341, n = 9683)
私钥: (d = 5581, n = 9683)

案例1第二次:输入Hello world! I am XuXuan!
生成参数如下:
生成的素数 p = 761, q = 877
生成的公钥指数 e = 6601
公钥: (e = 6601, n = 667397)
私钥: (d = 237721, n = 667397)

案例1第三次:输入Hello world! I am XuXuan!
生成参数如下:
生成的素数 p = 751, q = 13
生成的公钥指数 e = 1957
公钥: (e = 1957, n = 9763)
私钥: (d = 4093, n = 9763)

案例2:输入QQQQ11112222WWWW
生成参数如下:
生成的素数 p = 941, q = 883
生成的公钥指数 e = 21793
公钥: (e = 21793, n = 830903)
私钥: (d = 805417, n = 830903)

案例3:输入RSAES-PKCS1-V1_5 填充机制测试3
生成参数如下:
生成的素数 p = 67, q = 433
生成的公钥指数 e = 9859
公钥: (e = 9859, n = 29011)
私钥: (d = 5515, n = 29011)

6. 源代码
6.1 无填充
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
// 米勒-拉宾素性测试
int miller_rabin_test(int n, int k) {
// 若 n 是偶数,直接返回 false
if (n == 2) return 1;
if (n < 2 || n % 2 == 0) return 0;
// 计算 n-1 = 2^s * d,其中 d 为奇数
int d = n - 1;
int s = 0;
while (d % 2 == 0) {
d /= 2;
s++;
}
// k 次测试
for (int i = 0; i < k; i++) {
// 生成随机数 a,1 <= a <= n-1
int a = rand() % (n - 1) + 1;
int x = 1;
for (int j = 0; j < d; j++) {
x = (x * a) % n;
}
if (x == 1 || x == n - 1) continue;
// 反复平方 a,直到得到 n-1 或者 x == 1
int r = 0;
for (int j = 0; j < s - 1; j++) {
x = (x * x) % n;
if (x == n - 1) break;
if (x == 1) return 0; // 不是素数
}
if (x != n - 1) return 0; // 不是素数
}
return 1; // 是素数
}
// 生成一个大素数
int generate_large_prime(int bit_length, int k) {
int num;
do {
// 随机生成一个大数
num = rand() % (1 << bit_length);
num |= 1; // 保证 num 是奇数
} while (!miller_rabin_test(num, k));
return num;
}
// 计算最大公约数(GCD)
int gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
// 快速模幂算法
long long mod_exp(long long base, long long exp, long long mod) {
long long result = 1;
base = base % mod;
while (exp > 0) {
if (exp % 2 == 1) {
result = (result * base) % mod;
}
exp = exp >> 1;
base = (base * base) % mod;
}
return result;
}
// 求模反元素 (扩展欧几里得算法)
int mod_inverse(int e, int phi) {
int t = 0, new_t = 1;
int r = phi, new_r = e;
while (new_r != 0) {
int quotient = r / new_r;
int temp_t = t;
t = new_t;
new_t = temp_t - quotient * new_t;
int temp_r = r;
r = new_r;
new_r = temp_r - quotient * new_r;
}
if (t < 0) t += phi;
return t;
}
// 随机生成 e 并确保 e 和 φ(n) 互质
int generate_e(int phi) {
int e;
do {
e = rand() % (phi - 2) + 2; // 随机生成 2 到 φ(n) - 1 之间的数
} while (gcd(e, phi) != 1); // 确保 e 和 φ(n) 互质
return e;
}
int main() {
srand(time(NULL)); // 使用当前时间作为随机数种子
// 1. 输入文本串 s
char s[128];
printf("请输入要加密的文本串 s: ");
fgets(s, sizeof(s), stdin);
s[strcspn(s, "\n")] = '\0'; // 移除换行符
int s_len = strlen(s);
// 动态分配内存
long long* encrypted = (long long*)malloc(s_len * sizeof(long long));
if (encrypted == NULL) {
printf("内存分配失败\n");
return -1;
}
char* decrypted = (char*)malloc((s_len + 1) * sizeof(char));
if (decrypted == NULL) {
printf("内存分配失败\n");
free(encrypted);
return -1;
}
// 2. 生成大素数 p 和 q
int p = generate_large_prime(10, 10); // 10 位数的素数
int q = generate_large_prime(10, 10); // 10 位数的素数
printf("生成的素数 p = %d, q = %d\n", p, q);
int n = p * q;
int phi = (p - 1) * (q - 1);
// 随机生成公钥指数 e
int e = generate_e(phi);
printf("生成的公钥指数 e = %d\n", e);
int d = mod_inverse(e, phi);
printf("生成的公钥: (e = %d, n = %d)\n", e, n);
printf("生成的私钥: (d = %d, n = %d)\n", d, n);
// 3. 加密文本
printf("加密结果: ");
for (int i = 0; i < s_len; i++) {
encrypted[i] = mod_exp(s[i], e, n); // 加密每个字符
printf("%lld ", encrypted[i]);
}
printf("\n");
// 4. 解密文本
printf("解密结果: ");
for (int i = 0; i < s_len; i++) {
decrypted[i] = mod_exp(encrypted[i], d, n); // 解密每个字符
printf("%c", decrypted[i]);
}
decrypted[s_len] = '\0'; // 添加字符串结束符
printf("\n");
// 5. 比较原文本和解密结果
if (strcmp(s, decrypted) == 0) {
printf("解密成功: 原文本和解密文本一致\n");
}
else {
printf("解密失败: 原文本和解密文本不一致\n");
}
// 释放动态内存
free(encrypted);
free(decrypted);
return 0;
}
6.2 RSAES-OAEP 填充机制
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
// 米勒-拉宾素性测试
int miller_rabin_test(int n, int k) {
// 若 n 是偶数,直接返回 false
if (n == 2) return 1;
if (n < 2 || n % 2 == 0) return 0;
// 计算 n-1 = 2^s * d,其中 d 为奇数
int d = n - 1;
int s = 0;
while (d % 2 == 0) {
d /= 2;
s++;
}
// k 次测试
for (int i = 0; i < k; i++) {
// 生成随机数 a,1 <= a <= n-1
int a = rand() % (n - 1) + 1;
int x = 1;
for (int j = 0; j < d; j++) {
x = (x * a) % n;
}
if (x == 1 || x == n - 1) continue;
// 反复平方 a,直到得到 n-1 或者 x == 1
int r = 0;
for (int j = 0; j < s - 1; j++) {
x = (x * x) % n;
if (x == n - 1) break;
if (x == 1) return 0; // 不是素数
}
if (x != n - 1) return 0; // 不是素数
}
return 1; // 是素数
}
// 生成一个大素数
int generate_large_prime(int bit_length, int k) {
int num;
do {
// 随机生成一个大数
num = rand() % (1 << bit_length);
num |= 1; // 保证 num 是奇数
} while (!miller_rabin_test(num, k));
return num;
}
// 计算最大公约数(GCD)
int gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
// 快速模幂算法
long long mod_exp(long long base, long long exp, long long mod) {
long long result = 1;
base = base % mod;
while (exp > 0) {
if (exp % 2 == 1) {
result = (result * base) % mod;
}
exp = exp >> 1;
base = (base * base) % mod;
}
return result;
}
// 求模反元素 (扩展欧几里得算法)
int mod_inverse(int e, int phi) {
int t = 0, new_t = 1;
int r = phi, new_r = e;
while (new_r != 0) {
int quotient = r / new_r;
int temp_t = t;
t = new_t;
new_t = temp_t - quotient * new_t;
int temp_r = r;
r = new_r;
new_r = temp_r - quotient * new_r;
}
if (t < 0) t += phi;
return t;
}
// 随机生成 e 并确保 e 和 φ(n) 互质
int generate_e(int phi) {
int e;
do {
e = rand() % (phi - 2) + 2; // 随机生成 2 到 φ(n) - 1 之间的数
} while (gcd(e, phi) != 1); // 确保 e 和 φ(n) 互质
return e;
}
int main() {
srand(time(NULL)); // 使用当前时间作为随机数种子
// 1. 输入文本串 s
char s[128];
printf("请输入要加密的文本串 s: ");
fgets(s, sizeof(s), stdin);
s[strcspn(s, "\n")] = '\0'; // 移除换行符
int s_len = strlen(s);
// 动态分配内存
long long* encrypted = (long long*)malloc(s_len * sizeof(long long));
if (encrypted == NULL) {
printf("内存分配失败\n");
return -1;
}
char* decrypted = (char*)malloc((s_len + 1) * sizeof(char));
if (decrypted == NULL) {
printf("内存分配失败\n");
free(encrypted);
return -1;
}
// 2. 生成大素数 p 和 q
int p = generate_large_prime(10, 10); // 10 位数的素数
int q = generate_large_prime(10, 10); // 10 位数的素数
printf("生成的素数 p = %d, q = %d\n", p, q);
int n = p * q;
int phi = (p - 1) * (q - 1);
// 随机生成公钥指数 e
int e = generate_e(phi);
printf("生成的公钥指数 e = %d\n", e);
int d = mod_inverse(e, phi);
printf("生成的公钥: (e = %d, n = %d)\n", e, n);
printf("生成的私钥: (d = %d, n = %d)\n", d, n);
// 3. 加密文本
printf("加密结果: ");
for (int i = 0; i < s_len; i++) {
encrypted[i] = mod_exp(s[i], e, n); // 加密每个字符
printf("%lld ", encrypted[i]);
}
printf("\n");
// 4. 解密文本
printf("解密结果: ");
for (int i = 0; i < s_len; i++) {
decrypted[i] = mod_exp(encrypted[i], d, n); // 解密每个字符
printf("%c", decrypted[i]);
}
decrypted[s_len] = '\0'; // 添加字符串结束符
printf("\n");
// 5. 比较原文本和解密结果
if (strcmp(s, decrypted) == 0) {
printf("解密成功: 原文本和解密文本一致\n");
}
else {
printf("解密失败: 原文本和解密文本不一致\n");
}
// 释放动态内存
free(encrypted);
free(decrypted);
return 0;
}
6.3 RSAES-PKCS1-V1_5 填充机制
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
// 米勒-拉宾素性测试
int miller_rabin_test(int n, int k) {
if (n == 2) return 1;
if (n < 2 || n % 2 == 0) return 0;
int d = n - 1, s = 0;
while (d % 2 == 0) { d /= 2; s++; }
for (int i = 0; i < k; i++) {
int a = rand() % (n - 1) + 1;
int x = 1;
for (int j = 0; j < d; j++) x = (x * a) % n;
if (x == 1 || x == n - 1) continue;
for (int r = 0; r < s - 1; r++) {
x = (x * x) % n;
if (x == n - 1) break;
if (x == 1) return 0;
}
if (x != n - 1) return 0;
}
return 1;
}
// 生成一个大素数
int generate_large_prime(int bit_length, int k) {
int num;
do {
num = rand() % (1 << bit_length) | 1;
} while (!miller_rabin_test(num, k));
return num;
}
// 计算最大公约数(GCD)
int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
// 快速模幂
long long mod_exp(long long base, long long exp, long long mod) {
long long result = 1;
while (exp > 0) {
if (exp % 2 == 1) result = (result * base) % mod;
base = (base * base) % mod;
exp /= 2;
}
return result;
}
// 求模反元素 (扩展欧几里得)
int mod_inverse(int e, int phi) {
int t = 0, new_t = 1, r = phi, new_r = e;
while (new_r != 0) {
int quotient = r / new_r;
int tmp = t; t = new_t; new_t = tmp - quotient * new_t;
tmp = r; r = new_r; new_r = tmp - quotient * new_r;
}
return (t < 0) ? t + phi : t;
}
// 随机生成 e 并确保与 phi 互质
int generate_e(int phi) {
int e;
do { e = rand() % (phi - 2) + 2; } while (gcd(e, phi) != 1);
return e;
}
// PKCS#1 v1.5 填充
void pkcs1_v1_5_pad(unsigned char* message, size_t mLen, unsigned char* padded, size_t k) {
if (mLen > k - 11) {
fprintf(stderr, "消息太长,无法填充\n");
exit(EXIT_FAILURE);
}
padded[0] = 0x00;
padded[1] = 0x02;
for (size_t i = 2; i < k - mLen - 1; i++) {
do { padded[i] = rand() % 256; } while (padded[i] == 0);
}
padded[k - mLen - 1] = 0x00;
memcpy(&padded[k - mLen], message, mLen);
}
// PKCS#1 v1.5 解填充
void pkcs1_v1_5_unpad(unsigned char* padded, size_t k, unsigned char* message, size_t* mLen) {
if (padded[0] != 0x00 || padded[1] != 0x02) {
fprintf(stderr, "解填充失败,格式错误\n");
exit(EXIT_FAILURE);
}
size_t start = 2;
while (start < k && padded[start] != 0x00) start++;
if (start == k) {
fprintf(stderr, "解填充失败,未找到结束标志\n");
exit(EXIT_FAILURE);
}
*mLen = k - start - 1;
memcpy(message, &padded[start + 1], *mLen);
}
int main() {
srand(time(NULL));
// 1. 输入文本
char s[128];
printf("请输入要加密的文本: ");
fgets(s, sizeof(s), stdin);
s[strcspn(s, "\n")] = '\0';
int s_len = strlen(s);
// 动态内存分配
int key_size = 64; // 模数位数(单位:字节)
unsigned char* padded_message = (unsigned char*)malloc(key_size);
long long* encrypted = (long long*)malloc(key_size * sizeof(long long));
if (!padded_message || !encrypted) {
fprintf(stderr, "内存分配失败\n");
return -1;
}
// 2. 生成大素数 p 和 q
int p = generate_large_prime(10, 10);
int q = generate_large_prime(10, 10);
printf("生成的素数 p = %d, q = %d\n", p, q);
int n = p * q, phi = (p - 1) * (q - 1);
// 随机生成 e 并计算 d
int e = generate_e(phi);
int d = mod_inverse(e, phi);
printf("生成的公钥指数 e = %d\n", e);
printf("公钥: (e = %d, n = %d)\n", e, n);
printf("私钥: (d = %d, n = %d)\n", d, n);
// 3. 填充并加密
pkcs1_v1_5_pad((unsigned char*)s, s_len, padded_message, key_size);
printf("加密结果: ");
for (int i = 0; i < key_size; i++) {
encrypted[i] = mod_exp(padded_message[i], e, n);
printf("%lld ", encrypted[i]);
}
printf("\n");
// 4. 解密并去除填充
printf("解密结果: ");
unsigned char* decrypted_message = (unsigned char*)malloc(key_size);
size_t decrypted_len;
for (int i = 0; i < key_size; i++) {
decrypted_message[i] = mod_exp(encrypted[i], d, n);
}
// 解填充
pkcs1_v1_5_unpad(decrypted_message, key_size, (unsigned char*)s, &decrypted_len);
printf("%s\n", (char*)s);
// 释放内存
free(padded_message);
free(encrypted);
free(decrypted_message);
return 0;
}




















 3866
3866

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








