C语言回溯法之马踏棋盘（最通俗易懂代码）

马踏棋盘问题是一个NP问题，可以用回溯法求解。普通循环迭代很难找到解，而回溯法通过递归尝试不同路径，在遇到死路时回退，最终找到可行解。本文通过C语言展示了如何应用回溯法解决这个问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

定义：

**
马踏棋盘问题是旅行商问题（TSP）或哈密顿回路问题（HCP）的一个特例。在 8×8（在本例中采用5*5）的象棋棋盘上，用一个马按照马步跳遍整个棋盘，要求每个格子都只跳到一次，最后回到出发点。这是一个 NP问题，通常采用回溯法或启发式搜索类算法求解。
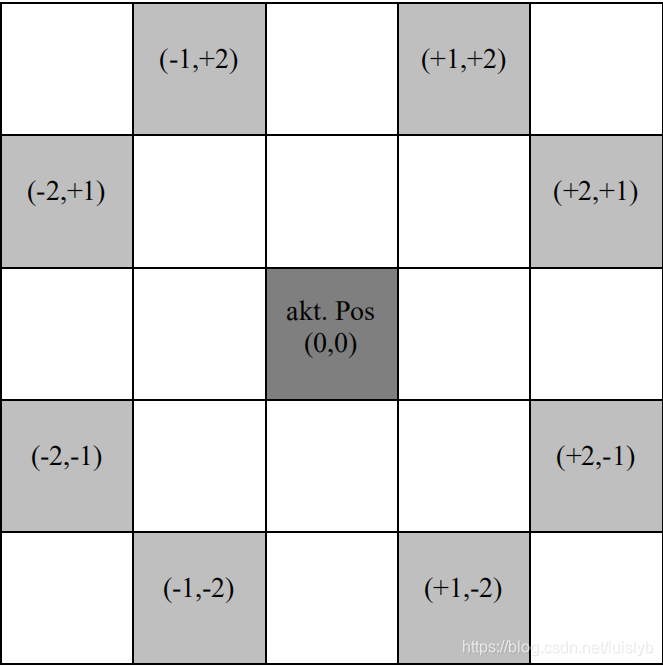
在这里插入图片描述

普通的循环迭代

若对该问题只进行普通的循环迭代，即每次循环都使用相同的判断条件，也只有极小概率能够一次将棋盘完全遍历（取决于起始点的位置以及判断的顺序）：
举例：
（假设以最中间点为起点，每次按照顺时针呢进行判断，若未被遍历则遍历该节点，即按照下图1->8的顺序进行）
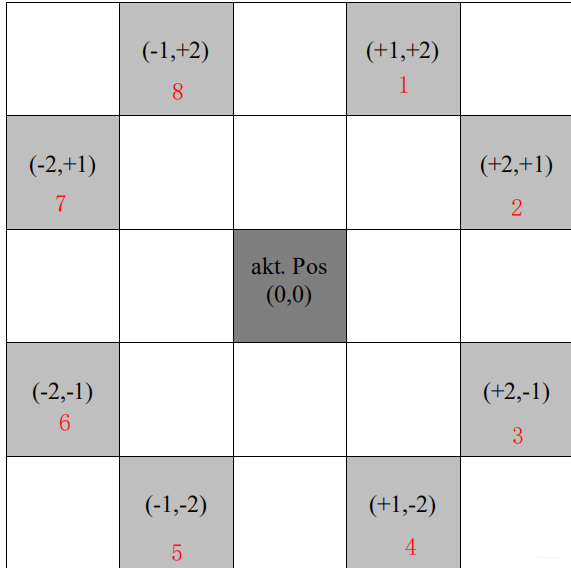
在这里插入图片描述
所得结果为：

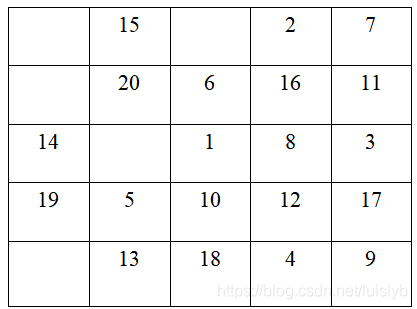
可见在遍历至20次时已无法继续遍历，但仍有结点为空；

解决方案：回溯法

例如图二，如果我们在20号结点遍历完成后发现马走到了死路，就退回到上一节点让马选择另一条路径，反复递归，最终即可得到结果：

#include<stdlib.h>
#include<stdio.h>
int chess[9][9];//定义棋盘,为什么5*5的棋盘要定义9*9的数组？
//如果只定义5*5的棋盘，则马位于5*5棋盘的边界时仍可能向边界外走，不符合题目要求
//马走的方向
int move[8][2] = {
   
    {
   
    2, 1 }, {
   
    1, 2 }, {
   
    -1, 2 }, {
   
    -2, 1 }, {
   
    -2, -1 },