Leetcode 42. 接雨水

Leetcode 42. 接雨水

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

题目分析

此题可以用暴力或者动态规划解。
分析动态规划的过程，一个位置能蓄多少水其实取决于此位置两边最高的两个柱子left_H和right_H。准确的说是left_H和right_H中较矮的那个。一个位置能蓄的水等于其与left_H和right_H中较矮的那个的差。如果本位置的高度高于min(left_H,right_H)，是蓄不了水的，会从矮的那边流光的。

动态规划的思路是，用两个数组分别记录位置i左右两边最高的柱子。
在更新数组的过程中，我们可以发现，其实我们并不关心left_H和right_H中高的那个，我们只关心矮的那个。

此时，我们可以用双指针的方式来简化算法。

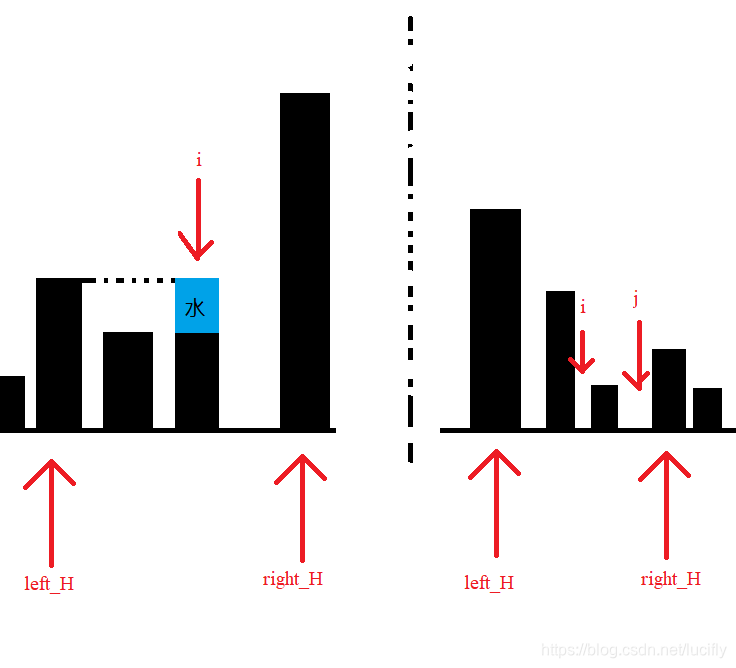
此时，我们分别从两端移动遍历数组。i从左往右，j从右往左。
此时有两种情况，

1. left_H < right_H
   此时，我们只关心 left_H和i，此时，无论i右侧的值是多少，i都能蓄left_H - heigh[i]。多了会从左侧流走。右侧最少有right_H挡着也不会少。
   当heigh[i] > left_H时，更新left_H到i。
2. left_H > right_H时同理。

代码

func trap(height []int) int {
    left_p, right_p := 0, len(height)-1
    total_w := 0
    i,j := 1, len(height)-2
    if len(height) < 2 {
        return 0
    }
    for ; left_p < right_p; {
        if height[left_p] < height[right_p] {
            if height[i] < height[left_p] {
                total_w += (height[left_p]-height[i])
            } else {
                left_p = i
            }
            i++
        } else {
            if height[j] < height[right_p] {
                total_w += (height[right_p]-height[j])
            } else {
                right_p = j
            }
            j--
        }

    }
    return total_w
}

数组每个位置只计算一遍，算法复杂度$O(n)$ 。