B - Berland Regional（前缀和优化）-优快云博客

该博客主要介绍了一种使用动态规划策略解决组合优化问题的方法。具体而言，它涉及一个地区内的学校，每个学校有一定数量的人，每个人都有不同的能力值。目标是组建不同规模的队伍（从1到n个人），使得队伍内所有人的能力值之和最大。博客通过输入数据，使用vector存储和前缀和技巧来实现动态规划求解，并给出了详细的代码实现过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

B - Berland Regional

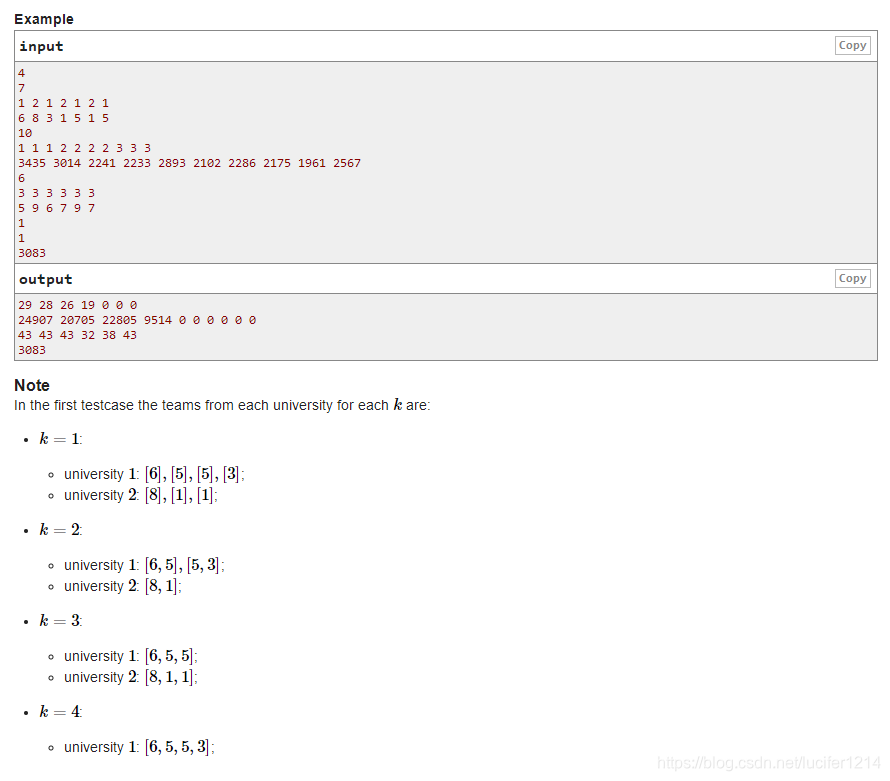
在这里插入图片描述

题目大意：
每个地区有 $n$ 个学校 $n$ 个人，每个人有一个能力值，要求组成 $k$ 人的队伍，k为 $1 - n$ 的所有数求队伍中所有人能力值的总和。
思路：
首先输入数据，按照学校标号，利用 $v e c t o r$ 进行存储，利用 $v e c t o r$ 按标号初始化前缀和数组，依次加入到答案数组中即可。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<cmath>
#include<iomanip>
#include<queue>
using namespace std;

typedef long long ll;
const int p = 1e9 + 7;
typedef pair<int, int> pii;
const int N = 1e6+10;

map<int, int>mp;
struct node {
	int id;
	ll sk;
}a[N];
int n;
vector<int>sum[N];
ll ans[N];
ll s[N];
bool cmp(int x, int y) {
	return x > y;

}
void init() {
	for (int i = 1; i <= n; i++) {
		sum[i].clear();
		ans[i] = 0;
	}
}
int main() {
	int t;
	cin >> t;
	while (t--)
	{
		init();
		cin >> n;
		ll ma = 0;
		for (int i = 1; i <= n; i++) cin >> a[i].id;
		for (int i = 1; i <= n; i++)cin >> a[i].sk;
		for (int i = 1; i <= n; i++)sum[a[i].id].push_back(a[i].sk);
		for (int i = 1; i <= n; i++) {
			int h = sum[i].size();
			if (h == 0)continue;
			sort(sum[i].begin(), sum[i].end(), cmp);
			for (int j = 1; j <= h; j++)
				s[j] = s[j - 1] + sum[i][j - 1];
			for (int j = 1; j <= h; j++)
				ans[j] += s[h / j * j];
		}
		cout << ans[1];
		for (int i = 2; i <= n; i++)cout << ' ' << ans[i];
		cout << endl;
	}
}