题目:定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的min函数。在该栈中,调用min,push及pop的时间复杂度都是O(1)
思路1:每次压入一个元素,将栈里面的元素进行相应的排序,将最小的元素放入栈顶(这样已经不符合栈的数据结构了,所以舍弃)
思路2:在栈里面申请一个单元用来存放最小的元素,第一次压进来的默认为最小的元素,然后每次压进来一个就和最小的进行更换,这样这个单元里面存的就是最小的了。(但是这种思路也有缺陷,就是说他可以保存最小的元素,但是不能保存次小的,如果是次小的话,那就没办法了)
思路3:既然思路2已经有大致的样子了,我们就顺着思路2的想法来,就是说在新的最小元素产生时,我们要把次小的保存起来,在这里那,我们就需要一个辅助栈了。
思路大概就是下面这样
步骤 | 操作 | 数据栈 | 辅助栈 | 最小值 |
1 | 压入3 | 3 | 3 | 3 |
2 | 压入4 | 3,4 | 3,3 | 3 |
3 | 压入2 | 3,4,2 | 3,3,2 | 2 |
4 | 压入1 | 3,4,2,1 | 3,3,2,1 | 1 |
5 | 弹出 | 3,4,2 | 3,3,2 | 2 |
6 | 弹出 | 3,4 | 3,3 | 3 |
7 | 压入0 | 3,4,0 | 3,3,0 | 0 |
代码:
package jzoffer;
import java.util.Stack;
public class MyStack {
private static Stack<Integer> mStack = new Stack<Integer>();
private static Stack<Integer> minStack = new Stack<Integer>();
public static void push(Integer i){
mStack.push(i);
if(minStack.size() == 0 || i<minStack.peek()){ //判断栈顶的元素
minStack.push(i);
}else{
minStack.push(minStack.peek());
}
}
public static void pop(){
assert(mStack.size()>0 && minStack.size()>0);//程序员自己写的断言
minStack.pop();
mStack.pop();
}
public static Integer min(){
assert(mStack.size() > 0 && minStack.size()>0);
return minStack.peek();
}
public static void main(String[] args) {
System.out.println("压入3");
push(3);
System.out.println("min:"+min());
System.out.println("压入4");
push(4);
System.out.println("min:"+min());
System.out.println("压入2");
push(2);
System.out.println("min:"+min());
System.out.println("压入1");
push(1);
System.out.println("min:"+min());
System.out.println("弹出");
pop();
System.out.println("min:"+min());
System.out.println("弹出");
pop();
System.out.println("min:"+min());
System.out.println("压入0");
push(0);
System.out.println("min:"+min());
}
}
结果图:
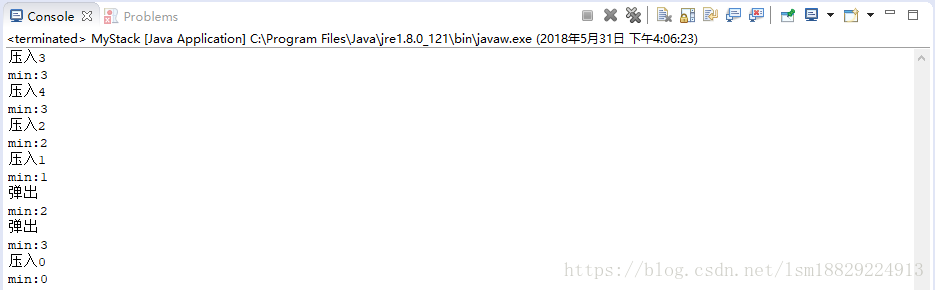








 本文介绍了一种特殊栈的设计方案,此栈包含一个min函数,可在O(1)时间复杂度内返回栈中最小元素。通过使用辅助栈保存每个状态下的最小值,确保常规栈操作如push和pop同样保持O(1)的时间复杂度。
本文介绍了一种特殊栈的设计方案,此栈包含一个min函数,可在O(1)时间复杂度内返回栈中最小元素。通过使用辅助栈保存每个状态下的最小值,确保常规栈操作如push和pop同样保持O(1)的时间复杂度。
















 380
380

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








