动态规划解决币值最大化问题

币值最大化

问题描述

• 给定一排n个硬币，其面值均为整数c1, c2, …, cn, 这些整数并不一定两两不同。问如何选择硬币，使得在其原始位置互不相邻的条件下，所选硬币的总金额最大。

解题思路

• 上述最大可选金额用f(n)表示，我们可以将所有可行的选择划分为两组：包括最后一枚硬币的和不包括最后一枚硬币的。第一组中，可选包含最后一枚硬币的，最大金额为Cn+f(n-2)，即最后一枚硬币加上前面n-2枚硬币可选的最大金额。按照f(n)的定义，另一组中可选的最大金额为f(n-1)，即前n-1枚硬币的最大金额。

• 可得出符合初始条件的递推方程：

f(n)=max{Cn+f(n-2),f(n-1)}
f(0)=0,f(1)=c1

• 再用回溯的方法得到获取最大值的各个币值

• 用币值大小为5 1 2 10 6 4 的几枚硬币为例子

• 通过上述方程列表：
  

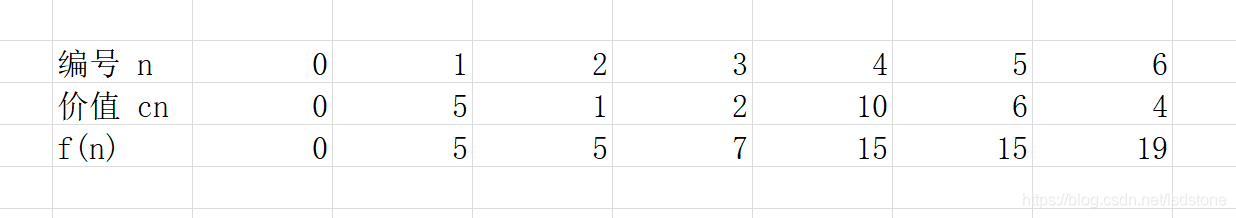
• 再通过回溯法得到所选择的硬币

• 分为两种情况，即选择了第n-1个和没选择第n-1个硬币，如果f(n)=f(n-1)则选择了第n-1个反之则没有选择第n-1个。

• 代码如下所示：

// a币值最大化.cpp : 定义控制台应用程序的入口点。
//

	#include "stdafx.h"
	#include"math.h"
	
	#define max(x,y)  (x>y)?x:y
	#define MAX 20
	int c[MAX];//代表价值
	int f[MAX];


	int coinmax(int n)
	{
		c[0] = 0;//初始化c[0]及f[0]
		f[0] = 0;
		f[1] = c[1];

		for (int i = 2; i <= n; i++)
		{
			f[i] = max(c[i] + f[i - 2], f[i - 1]);
				//获取最大币值

		}
		return f[n];

	}



	int main()
	{

		int n;
		printf("请输入有多少个纸币：");
		scanf("%d", &n);
		printf("请分别输入纸币的价值：");
		for (int i = 1; i <= n; i++)
		{
			scanf("%d", &c[i]);

		}
		int arr[MAX];//定义arr数组表示所选择的硬币
		int num = 0;
		printf("最大币值为：%d\n", coinmax(n));
		for (int i = n; i >= 1; i--)
		{
			if (f[i] == f[i - 1])//选择了第i-1个，然后再将第i-1个放进arr数组
			{
				arr[num++] = c[--i];

			}

			else{
				arr[num++] = c[i--];//没有选择第i-1个则将他本身先放入数组，
				               //然后再将数组c的下标减一，arr的下标加一

			}


		}
		printf("各个币值为：");
		for (int i = 0; i<num; i++)

			printf("%d ", arr[i]);




	}

• 运行结果如下：