Problem Description
Function Fx,ysatisfies:
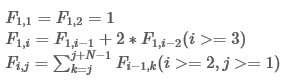
For given integers N and M,calculate Fm,1 modulo 1e9+7.
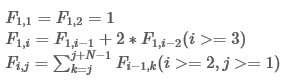
For given integers N and M,calculate Fm,1 modulo 1e9+7.
Input
There is one integer T in the first line.
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.
Output
For each given N and M,print the answer in a single line.
Sample Input
2 2 2 3 3
Sample Output
2 33
推导如下
F1i=2^i-(-1)^i/3
Fij=F(i+n)-F(i)
Fm1=sum(C(m-1,i)*2^i*(-1)^(m-1-i))
=(2*(2^n-1)^(m-1)+n%2)/3
#include<map>
#include<cmath>
#include<queue>
#include<vector>
#include<cstdio>
#include<string>
#include<cstring>
#include<cassert>
#include<iostream>
#include<algorithm>
using namespace std;
long long mod=1000000007;
inline long long power(long long x,long long y)
{
long long t=1;
while(y!=0)
{
if(y%2==1)
t=t*x%mod;
x=x*x%mod;
y/=2;
}
return t;
}
int main()
{
int T;
scanf("%d",&T);
while(T>0)
{
T--;
long long n,m;
scanf("%lld%lld",&n,&m);
long long ans=power(2,n)-1LL;
ans=power(ans,m-1);
ans=ans*2LL%mod;
ans+=n%2;
long long xt=power(3,mod-2);
ans=ans*xt%mod;
printf("%lld\n",ans);
}
return 0;
}
Problem Description
Function Fx,ysatisfies:
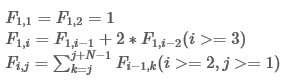
For given integers N and M,calculate Fm,1 modulo 1e9+7.
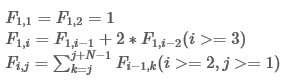
For given integers N and M,calculate Fm,1 modulo 1e9+7.
Input
There is one integer T in the first line.
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.
Output
For each given N and M,print the answer in a single line.
Sample Input
2 2 2 3 3
Sample Output
2 33





 本文介绍了一种计算特定函数Fm,1值的方法,该函数满足一定递推关系,针对给定的大整数N和M,通过快速幂运算求解该函数模1e9+7的结果。
本文介绍了一种计算特定函数Fm,1值的方法,该函数满足一定递推关系,针对给定的大整数N和M,通过快速幂运算求解该函数模1e9+7的结果。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








