整数划分（C语言）

整数划分问题：把整整数n拆分成n=k1+k2+k3....,其中k为正整数，求一共有多少种划分

例如，正整数6有如下11种划分:

6;

5+1;

4+2,4+1+1;

3+3,3+2+1,3+1+1+1;

2+2+2,2+2+1+1,2+1+1+1+1;

1+1+1+1+1+1;

用递归思想求解：

定义递归函数f(n,max)，表示对整数n进行划分，返回所有划分种类中，最大值不超过max的划分个数。(我们先假设这个函数就能实现这个功能)

举个例子f(5,3),有如下划分：3+2、3+1+1、2+2+1、1+1+1+1+1，返回4，即对整数5进行划分，其中最大值不超过3的所有划分一共有4个，（反例:4+1也可以是整数5的划分，但这个划分中最大值为4，超过了3，所以不属于f(5,3)）

明白了这个递归函数的意义，那么接下来就很容易理解，分以下这几种情况讨论

1.当n=1时，不管max的值为多少，都只有一种划分，即 1,返回1

2.当max=1时，不管n的值为多少，都只有一个划分，返回1（例如n=4,max=1，划分为：1+1+1+1）

3.当max>n时,因为对于每种划分，加起来的值都要等于n，所以划分中的最大值不能超过n,

所以返回 f(n,n);

4.当max=n时，此时分两种情况，一种是最大值包含n，当然最大值包含n的划分只有1个，另外一种是最大值不包含n，说白了就是最大值<=n-1,对应的函数就是f(n,n-1)，所以两种情况加起来就是返回 1+f(n,n-1);

5.当max<n时，此时也分两种情况，一种是最大值包含max，意味着这种划分中至少包含1个max，那么剩下就只需要对n-max进行划分，即f(n-max,max);另一种是最大值不包含max，说白了就是最大值<=max-1

翻译成对应的函数就是f(n,max-1)     所以把这两种情况加起来就是返回 f(n-max,max)+f(n,max-1);

代码如下：

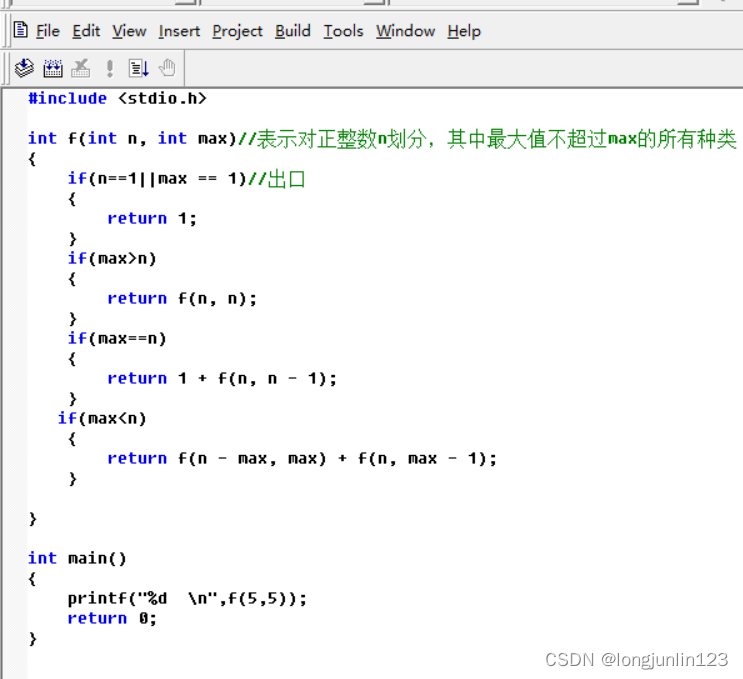
如果有不理解请再看看递归函数f(n,max)的定义：表示对整数n进行划分，返回所有划分种类中，最大值不超过max的划分个数