斜率优化DP：打印文档(模板）

时间限制 : 1 秒

内存限制 : 128 MB

零有一台旧打印机，它有时运转得不太好。尽管这是一台老式打印机了，但他仍然喜欢用它来打印文章。然而，这台打印机太旧了，无法长时间工作，而且肯定会出现磨损，所以零用一个成本数值来衡量这种磨损程度。 有一天，零想要打印一篇有N个单词的文章，并且每个单词i都有一个打印成本Ci。此外，零知道在一行中打印k个单词的成本是M（M是一个常量数值）。

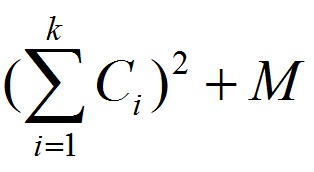
现在零想知道，为了完美地排版这篇文章，所需的最小成本是多少。分享零应该如何计算打印这篇文章的最小成本？有没有其他方法可以降低打印这篇文章的成本？如果打印机的磨损程度增加，最小成本会如何变化？

输入

有许多测试用例。对于每个测试用例，第一行有两个数字N和M,(0<=n<=500000)，(0<=M<=1000)）。然后，在接下来的第2行到第N + 1行中有N个数字。输入以文件结束符（EOF）终止。

输出

一个单独的数字，表示打印这篇文章的最小成本。

样例

输入

5 5
5
9
5
7
5

输出

230

———————————————————————————————————————————

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+2;
long long a[N],sum[N],dp[N];
int n,m;
int main()
{
	while(cin>>n>>m)
	{
		for(int i=1;i<=n;i++)
		{
			cin>>sum[i];
			sum[i]+=sum[i-1];		
		}
		int l=0,r=1;
		for(int i=1;i<=n;i++)
		{
			//若(dp[j]+sum[j]^2-dp[k]-sum[k]^2)/(sum[j]-sum[k])<=2*sum[i]
			//则说明k比j更优，可以将淘汰j 这里(j=a[l],k=a[l+1])
			while(l<r)//维护队头 
			{
				int j=a[l],k=a[l+1];
				if(dp[k]+sum[k]*sum[k]-dp[j]-sum[j]*sum[j]<=2*sum[i]*(sum[k]-sum[j])) l++; 
				else break;
			}
			dp[i]=dp[a[l]]+(sum[i]-sum[a[l]])*(sum[i]-sum[a[l]])+m;
			while(l<r)//维护队尾 
			{
				int j=a[r],k=a[r-1];
				if(dp[j]+sum[j]*sum[j]-dp[k]+sum[k]*sum[k]*(sum[i]-sum[j])>=(dp[i]+sum[i]*sum[i]-dp[j]-sum[j]*sum[j])*(sum[j]-sum[k])) r--;
				else break;
				
			}
			a[++r]=i;
		}
		cout<<dp[n]<<endl;
		memset(dp,0,sizeof(dp));
		memset(a,0,sizeof(a));
	}
	return 0;
}