P1219 [USACO1.5] 八皇后 Checker Challenge

题目描述

一个如下的 6×6 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

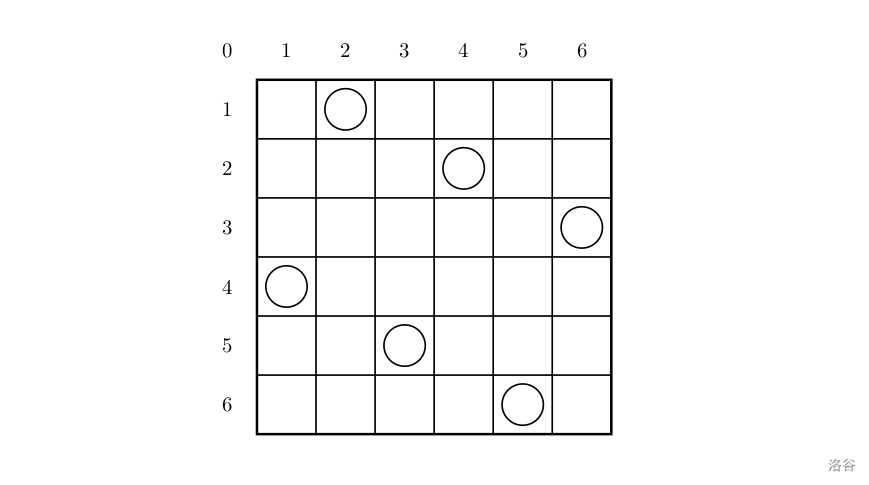
上面的布局可以用序列 2 4 6 1 3 5来描述，第 i 个数字表示在第 i 行的相应位置有一个棋子，如下：

行号 1 2 3 4 5 6

列号 2 4 6 1 3 5

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。

输入格式

一行一个正整数 n，表示棋盘是 n×n 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入输出样例

输入 #1

6

输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

说明/提示

【数据范围】
对于 100% 的数据，6≤n≤13。

题目翻译来自NOCOW。

USACO Training Section 1.5

 解析

1,1	1,2	1,3	1,4	1,5	1,6
2,1	2,2	2,3	2,4	2,5	2,6
3,1	3,2	3,3	3,4	3,5	3,6
4,1	4,2	4,3	4,4	4,5	4,6
5,1	5,2	5,3	5,4	5,5	5,6
6,1	6,2	6,3	6,4	6,5	6,6

右对角线：下标差值相等（x+y+n）

深绿：x-y=5

淡黄：x-y=4

黑：x-y=3

淡蓝：x-y=2

深黄：x-y=1

红：x-y=0

橙：x-y=-1

淡绿：x-y=-2

深蓝：x-y=-3

紫：x-y=-4

灰：x-y=-5

那么所有下标的差值就是：-5，-4，-3，-2，-1，0，1，2，3，4，5

也就是：-(n-1)，-(n-2)， ……， 0，……， (n-1)

因为负数有不好计算等缺点所以让它们全部加n：1，2，3，……，2n-1

最后，就变成了：（x-y+n）

1,1	1,2	1,3	1,4	1,5	1,6
2,1	2,2	2,3	2,4	2,5	2,6
3,1	3,2	3,3	3,4	3,5	3,6
4,1	4,2	4,3	4,4	4,5	4,6
5,1	5,2	5,3	5,4	5,5	5,6
6,1	6,2	6,3	6,4	6,5	6,6

左对角线：下标和不变 

深绿：x+y=2

淡黄：x+y=3

黑：x+y=4

淡蓝：x+y=5

深黄：x+y=6

红：x+y=7

橙：x+y=8

淡绿：x+y=9

深蓝：x+y=10

紫：x+y=11

灰：x+y=12

这个就很简单了：（x+y）

代码

#include<bits/stdc++.h>
using namespace std;
bool C[20],RD[30],LD[30];//column（列），right diagonal（右对角线），left diagonal（左对角线 ） 
int n,cnt,ans[20];
void dfs(int cur){
	if(cur==n+1){
		cnt++;
		if(cnt<=3){
			for(int i=1;i<=n;i++){
				cout<<ans[i]<<" ";
			}
			cout<<endl;
		}
	}else{
		for(int i=1;i<=n;i++){//cur行i列
			if(C[i]==0 && RD[cur-i+n]==0 && LD[cur+i]==0){
				ans[cur]=i;
				C[i]=1;
				RD[cur-i+n]=1;
				LD[cur+i]=1;
				dfs(cur+1);
				C[i]=0;
				RD[cur-i+n]=0;
				LD[cur+i]=0;
			}
		}
	}
}
int main() {
	cin>>n;
	dfs(1);
	cout<<cnt;
	return 0;
}

\(^o^)/~