Light OJ 1028

最新推荐文章于 2019-03-29 20:38:00 发布

原创最新推荐文章于 2019-03-29 20:38:00 发布 · 179 阅读

0 ·

CC 4.0 BY-SA版权

数论专栏收录该内容

19 篇文章

订阅专栏

题目链接：Light OJ 1028

题目大意：给定一个数 n 求有多少种进制满足转换成该进制后最后一项为 0 ；

思路：本题的思路就是求 n 的因数的个数！

根据算数基本定理知道，对于每个整数n，都可以唯一分解成素数的乘积：

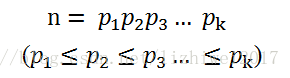
这里的素数并不要求是不一样的，所以可以将相同的素数进行合并，采用素数幂的乘积进行表示：

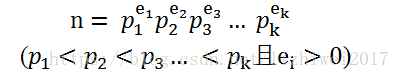
则因子的个数为 $N = (1 + e_{1}) * (1 + e_{2} ) * ... * (1 + e_{k})$

所有因数之和

$sum = (1 +p_{1} + p_{1}^{2} + p_{1}^{3} + ... + p_{1}^{e_{1}})* (1 +p_{2} + p_{2}^{2} + p_{2}^{3} + ... + p_{2}^{e_{2}}) *...*(1 +p_{r} + p_{r}^{2} + p_{r}^{3} + ... + p_{r}^{e_{r}})$

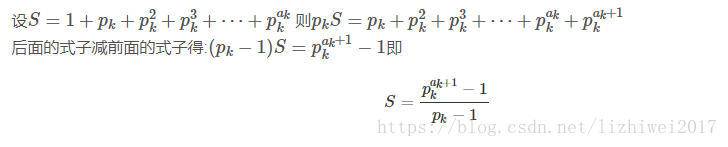
模板代码如下：

const int maxn = 1000000+10;
int prime[maxn];
bool is_prime[maxn];
int sieve(int n)//返回n以内素数的个数
{
    int p = 0;
    for(int i = 0; i <= n; i++)is_prime[i] = 1;
    is_prime[0] = is_prime[1] = 0;
    for(ll i = 2; i <= n; i++)
    {
        if(is_prime[i])
        {
            prime[p++] = i;
            for(ll j = i * i; j <= n; j += i)is_prime[j] = 0;//这里涉及i*i,必须使用long long
        }
    }
    return p;
}

ll Divisors_num(ll n, int tot)//素数总数
{
    ll ans = 1;
    for(int i = 0; i < tot && prime[i] * prime[i] <= n; i++)
    {
        if(n % prime[i] == 0)
        {
            int cnt = 0;
            while(n % prime[i] == 0)
            {
                cnt++;
                n /= prime[i];
            }
            ans *= (cnt + 1);
        }
    }
    if(n > 1)ans *= 2;
    return ans;
}
ll pow(ll a, ll b)
{
    ll ans = 1;
    while(b)
    {
        if(b & 1)ans = ans * a;
        a *= a;
        b /= 2;
    }
    return ans;
}
ll Divisors_sum(ll n, int tot)
{
    ll ans = 1;
    for(int i = 0; i < tot && prime[i] * prime[i] <= n; i++)
    {
        if(n % prime[i] == 0)
        {
            int cnt = 0;
            while(n % prime[i] == 0)
            {
                cnt++;
                n /= prime[i];
            }
            ans = (pow(prime[i], cnt + 1) - 1) / (prime[i] - 1) * ans;
        }
    }
    if(n > 1)ans *= (n + 1);
    return ans;
}

因子和

因子和详解