JZOJ 5898. 【NOIP2018模拟10.6】距离统计

最新推荐文章于 2018-10-31 22:19:20 发布

Felix-Lee

最新推荐文章于 2018-10-31 22:19:20 发布

阅读量200

点赞数 1

CC 4.0 BY-SA版权

分类专栏：图论点分树点分治文章标签：图论点分树点分治

本文链接：https://blog.youkuaiyun.com/liyizhixl/article/details/83051553

图论同时被 3 个专栏收录

84 篇文章

订阅专栏

点分树

1 篇文章

订阅专栏

点分治

1 篇文章

订阅专栏

本文介绍了一种基于点分树的数据结构算法，用于解决特定类型的路径查询问题。通过使用点分治策略，构建点分树，记录节点到其子树内所有节点的距离，并进行排序。在处理查询时，采用二分查找来确定距离小于等于给定值的节点数量，同时处理重复计算的问题。算法的时间复杂度为O(nlog³n)，适用于大规模图的路径查询。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Description

Input

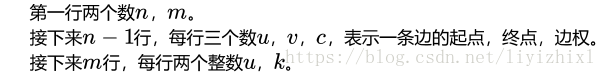
Output

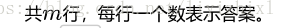
Sample Input

5 3
1 2 3
1 3 1
2 4 4
2 5 2
1 2
3 3
5 1

Sample Output

3
6
2

Data Constraint

Solution

这题用到点分树，即点分治时重心（前面的连向后面的）建成的树。
在每个点上记录一个数组 $f$ ，保存该点子树里的点到其距离（原树，包括自己），并排好序。
询问要二分答案 $k$ ，并判断有多少个点的距离 $≤k\leq k$ 即可。
那么询问时从该点开始往点分树的父亲上走，每次加上符合的个数（在数组 $f$ 里二分即可）。
但是这样会算重，即从点分树父亲那儿走到自己的答案可能算重了，我们需要减去一些。
于是再开一个数组 $g$ ，记录一个点子树里（原树，包括自己）到其点分树父亲的距离。
在排好序的数组 $g$ 里二分算重的个数并减去即可。
询问时二分答案、在点分树上往父亲跳、在数组里二分计算的复杂度均为 $n)O(log\ n)$ 。
总时间复杂度为 $O(n\log^3n)$ 。

Code

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>
#include<cctype>
using namespace std;
const int N=5e4+5;
int n,tot,node,mx,dep,dis,siz;
int first[N],nex[N<<1],en[N<<1],w[N<<1];
int first1[N],nex1[N],en1[N];
int fa[N],f[N],size[N],h[N][16],len[N][16],deep[N],dp[N],pre[N][20];
bool bz[N];
vector<int>g[N],d[N];
inline int read()
{
    int X=0,w=0; char ch=0;
    while(!isdigit(ch)) w|=ch=='-',ch=getchar();
    while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
    return w?-X:X;
}
void write(int x)
{
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
inline int max(int x,int y)
{
	return x>y?x:y;
}
inline void insert(int x,int y,int z)
{
	nex[++tot]=first[x];
	first[x]=tot;
	en[tot]=y;
	w[tot]=z;
}
inline void insert1(int x,int y)
{
	nex1[++tot]=first1[x];
	first1[x]=tot;
	en1[tot]=y;
}
void find(int x,int y,int z)
{
	size[x]=1;
	f[x]=0;
	for(int i=first[x];i;i=nex[i])
		if(en[i]^y && !bz[en[i]])
		{
			find(en[i],x,z+w[i]);
			size[x]+=size[en[i]];
			f[x]=max(f[x],size[en[i]]);
		}
	f[x]=max(f[x],siz-size[x]);
	if(f[x]<mx) mx=f[node=x],dep=z;
}
void down(int x,int y,int rt,int z)
{
	g[rt].push_back(z);
	for(int i=first[x];i;i=nex[i])
		if(en[i]^y && !bz[en[i]]) down(en[i],x,rt,z+w[i]);
}
void dfs(int x,int y)
{
	bz[x]=true;
	if(fa[x]=y) insert1(y,x);
	int siz1=siz;
	for(int i=first[x];i;i=nex[i])
		if(!bz[en[i]])
		{
			if(size[x]<size[en[i]]) siz=siz1-size[x]; else siz=size[en[i]];
			mx=siz;
			find(en[i],x,w[i]);
			down(node,0,node,0);
			dfs(node,x);
		}
}
void get(int x,int y,int z)
{
	if(z>dis) dis=z,node=x;
	for(int i=first[x];i;i=nex[i])
		if(en[i]^y)
		{
			if(en[i]>1 && !h[en[i]][0])
			{
				h[en[i]][0]=x;
				len[en[i]][0]=w[i];
				deep[en[i]]=deep[x]+1;
			}
			get(en[i],x,z+w[i]);
		}
}
inline int calc(int x,int y)
{
	if(deep[x]<deep[y]) swap(x,y);
	int s=0;
	for(int i=log2(deep[x]);i>=0;i--)
		if(deep[h[x][i]]>=deep[y])
		{
			s+=len[x][i];
			x=h[x][i];
		}
	if(x==y) return s;
	for(int i=log2(deep[x]);i>=0;i--)
		if(h[x][i]^h[y][i])
		{
			s+=len[x][i]+len[y][i];
			x=h[x][i];
			y=h[y][i];
		}
	s+=len[x][0]+len[y][0];
	return s;
}
void dg(int x)
{
	dp[x]=dp[fa[x]]+1;
	for(int y=fa[x],l=x;y;l=y,y=fa[y])
	{
		int z=calc(x,y);
		pre[x][dp[y]]=z;
		if(l) d[l].push_back(z);
	}
	for(int i=first1[x];i;i=nex1[i])
		if(en1[i]^fa[x]) dg(en1[i]);
}
int main()
{
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	n=read();
	int m=read();
	for(int i=1;i<n;i++)
	{
		int x=read(),y=read(),z=read();
		insert(x,y,z);
		insert(y,x,z);
	}
	get(deep[1]=1,0,0);
	get(node,0,0);
	for(int j=1;j<16;j++)
		for(int i=1;i<=n;i++)
		{
			h[i][j]=h[h[i][j-1]][j-1];
			len[i][j]=len[i][j-1]+len[h[i][j-1]][j-1];
		}
	tot=0;
	mx=siz=n;
	find(1,0,0);
	down(node,0,node,0);
	dfs(node,0);
	for(int i=1;i<=n;i++)
		if(!fa[i])
		{
			node=i;
			break;
		}
	dg(node);
	for(int i=1;i<=n;i++) g[i].push_back(dis);
	for(int i=1;i<=n;i++) sort(g[i].begin(),g[i].end());
	for(int i=1;i<=n;i++) d[i].push_back(dis);
	for(int i=1;i<=n;i++) sort(d[i].begin(),d[i].end());
	/*for(int j=1;j<=n;j++,putchar('\n'))
		for(int i=0;i<(int)g[j].size();i++) printf("%d ",g[j][i]);*/
	while(m--)
	{
		int u=read(),k=read()+1;
		int l=1,r=dis,ans=0;
		while(l<=r)
		{
			int mid=l+r>>1;
			int sum=upper_bound(g[u].begin(),g[u].end(),mid)-g[u].begin();
			for(int x=u;x^node;x=fa[x])
			{
				int lim=pre[u][dp[fa[x]]];
				if(lim>mid) continue;
				sum+=upper_bound(g[fa[x]].begin(),g[fa[x]].end(),mid-lim)-g[fa[x]].begin();
				sum-=upper_bound(d[x].begin(),d[x].end(),mid-lim)-d[x].begin();
			}
			if(sum>=k)
			{
				ans=mid;
				r=mid-1;
			}else l=mid+1;
		}
		write(ans),putchar('\n');
	}
	return 0;
}