背包问题6（dp

“所有的DP问题，本质上都是有限集中的最值问题”—yxc 

 图源（本文（01背包）借鉴处

---

01背包 

思路分析

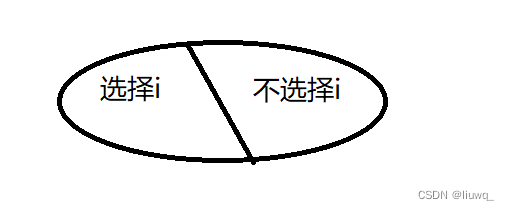
对于每一件物品我们都有选或者不选两种情况，因此一共有2^n种情况。

据闫氏dp分析法，将这2^n种情况看作一个集合f[]，需要找到集合中价值最大的情况；

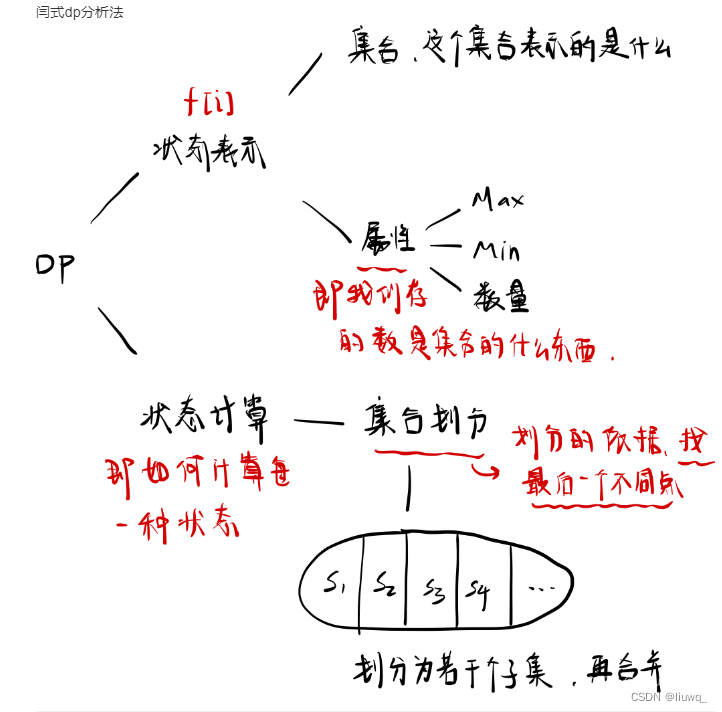
状态表示

f[i][j]意义：表示所有选法集合中（集合划分）,只从前i个物品中选,并且总体积≤j的选法的集合,它的值是这个集合中每一个选法的最大值.

属性：Max最大价值

状态计算

划分集合=>寻找最后一个不同点 ：是否选择第i个物品·

因此将集合划分为

#include <bits/stdc++.h>
using namespace std;
int f[1005][1005];//f[i][j]表示前i件物品在j个空间内能获得的最大价值 
int v[1005],w[1005];
int main(){
  int m,n;
  cin>>n>>m;
  for(int i=1;i<=n;i++){
    cin>>v[i]>>w[i];
}
  for(int i=1;i<=n;i++){
    for(int j=0;j<=m;j++){
      f[i][j]=f[i-1][j];//将之前的结果先复制到当前这次
      if(v[i]<=j) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);//存入最大的价值结果
    }
}
  cout<<f[n][m];
  return 0;
}

能否进行优化？

 但是此时，我们相当于用的是 f [ i ][ j - v[ i ] ]的状态，而并非 f [ i - 1][ j - v[ i ] ]的状态，因为 f [ i ] 把 f [ i - 1]的状态更新了。

因此，我们要想使用上一层的 j - v[i]，就需要把 j 逆序遍历。

#include<iostream>
using namespace std;

const int N = 1010;
int n,m;
int v[N],w[N];
int f[N];

int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i++) cin >> v[i] >> w[i];

    for(int i = 0; i <= n; i++) 
        for(int j = m; j >= v[i]; j--) 
            f[j] = max(f[j], f[j-v[i]]+w[i]);

    cout << f[m]<< endl;
    return 0;
}

作者：Cloudddddd
链接：https://www.acwing.com/solution/content/78621/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。