七段码--蓝桥杯

题目

小蓝要用七段码数码管来表示一种特殊的文字。

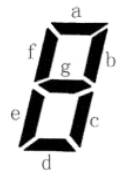
上图给出了七段码数码管的一个图示，数码管中一共有 77 段可以发光的二 极管，分别标记为 a, b, c, d, e, f, g。

小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符 的表达时，要求所有发光的二极管是连成一片的。

例如：b 发光，其他二极管不发光可以用来表达一种字符。

例如 c 发光，其他二极管不发光可以用来表达一种字符。这种方案与上 一行的方案可以用来表示不同的字符，尽管看上去比较相似。

例如：a, b, c, d, e 发光，f, g 不发光可以用来表达一种字符。

例如：b, f发光，其他二极管不发光则不能用来表达一种字符，因为发光 的二极管没有连成一片。

请问，小蓝可以用七段码数码管表达多少种不同的字符？

解题：

1.数据（各个二极管的开关情况）存储。因为二极管只有开关两种情况，即用0，1进行二进制存储。二全亮的时为1111111（2进制）即127（十进制），由题至少要有一个二极管发光。因此总情况是

=127

2.由于题中要求在设计字符 的表达时，要求所有发光的二极管是连成一片的。故需要对其中某一发光二极管进行深度优先搜索，并在到达的发光二极管处进行标记，当有二极管发光却未被标记时，这该情况不符题意，由总情况数减一；

3.此时我们便遇到一个问题，如何将连接情况进行存储呢

，以1表示相连，以0表示为相连和相同的数

	a	b	c	d	e	f	g
a	0	1	0	0	0	1	0
b	1	0	1	0	0	0	1
c	0	1	0	1	0	0	1
d	0	0	1	0	1	0	0
e	0	0	0	1	0	1	1
f	1	0	0	0	1	0	1
g	0	1	1	0	1	1	0

4.在二进制数中，%2取一位，/2去一位；

代码：

#include<bits/stdc++.h>
using namespace std;
int g[7][7] = {
    {0,1,0,0,0,1,0},
    {1,0,1,0,0,0,1},
    {0,1,0,1,0,0,1},
    {0,0,1,0,1,0,0},
    {0,0,0,1,0,1,1},
    {1,0,0,0,1,0,1},
    {0,1,1,0,1,1,0}
};
int bright[7];
int vis[7];
void dfs(int stick)
{
    for (int i = 0; i < 7; i++)
    {
        if (g[stick][i] && bright[i] && !vis[i])
        {
            vis[i] = 1;
            dfs(i);
        }
    }
    return ;
}
int main()
{
    int i, j, stick, x, ans = 127;
    for (i = 1; i <= 127; i++)
    {
        memset(bright, 0, sizeof(bright));
        memset(vis, 0, sizeof(vis));
        x = i; j = 0;
        while (x)
        {
            if (x % 2)bright[j] = 1;
            x /= 2; j++;
        }
        stick = 0;
        while (!bright[stick])stick++;
        vis[stick] = 1;
        dfs(stick);
        for (j = 0; j < 7; j++)
        {
            if (bright[j] && !vis[j])
            {
                ans--;
                break;
            }
        }
    }
    cout << ans << endl;
    return 0;
}