单调栈解决最大/最小子序列问题

两个数组中最大。。。

可以分别求两个数组的各自最大，然后合并两个一个数组中最大即可，两个数组一共要保留 k 个数字，则若 nums1 保留 i 个，则 nums2 保留 k - i 个，而对于 nums1 ，i 的取值范围应为多少呢？设 nums1 有 m 个元素，nums2 有 n 个元素

• 当 nums2 元素全部保留时，nums1 保留的元素的最少，为 k - n 个；
• 当 nums1 元素尽可能全保留而不保留 nums2 时，nums1 保留元素最多，为 k 或 m 个。

所以 i 的取值范围应该为：
$$i\in [max(0,k-n),min(k,m)]$$
剩下的主要问题就是：

• 如何保留一个数组中最大？
• 如何合并两个一个数组中最大？即两个数组的比较策略。

保留一个数组中的最大子序列

对于保留一个数组中最大子序列，其实就是402. 移掉K位数字题，让我们先来看下402题是如何解决的：
一个数组中取最小。。。

对于两个相同长度的数字序列，最左边不同的数字决定了这两个数字的大小，例如，对于 A = 12axx，B = 12bxx，如果 a > b 则 A > B。故若要使得剩下的数字最小，需要保证靠前的数字尽可能小。所以可以得到贪心策略：

对于一个长度为 n 的数字字符序列 num，从左向右找到第一个 i（i > 0），使得 nums[i - 1] > nums[i]，则将 nums[i - 1] 删掉，以此方法共删去 k 个该情况即可，若是没有该情况，则数字字符序列是严格升序，则从尾部删除即可。

上面的贪心分析是分析如何删除元素，实现的话需要 O(n * k) 的时间复杂度（要删除 k 个数，每次删除都需要遍历一趟），可以逆向思维，即如何保留元素，可以看到剩余的结果元素应该是单调不降的，这就很容易想到单调栈，维护一个单调栈，该栈维护当前的结果序列，也就是当前保留的元素，则应该一直维持栈内元素单调不降，所以对于每个数字，如果该数字小于栈顶元素，我们就不断地弹出栈顶元素，直到

• 栈为空
• 或者新的栈顶元素不大于当前数字
• 或者我们已经删除了 k 位数字

如对于例子 1432219，其栈的维护过程如下：

注意上述步骤结束后还需要针对一些情况做额外的处理：

• 若删除了 m 个数字且 m<k，则需要从序列尾部删除额外的 k-m 个数字；
• 若最终的数字序列存在前导零，则需要删去前导零；
• 若最终数字序列为空，则应该返回 "0"。

class Solution {
    public String removeKdigits(String num, int k) {
        Deque<Character> deque = new LinkedList<>();
        for (char cur : num.toCharArray()) {
            while (!deque.isEmpty() && k > 0 && deque.peekLast() > cur) {
                deque.pollLast();
                k--;
            }
            deque.offerLast(cur);
        }
        
        while (k > 0) {
            deque.pollLast();
            k--;
        }
        
        while (!deque.isEmpty() && deque.peekFirst() == '0') {
            deque.pollFirst();
        }
        
        StringBuilder res = new StringBuilder();
        while (!deque.isEmpty()) {
            res.append(deque.pollFirst());
        }
        
        return res.length() == 0 ? "0" : res.toString();
    }
}

合并两个最大子序列

设有如下两个最大子序列

[9, 6, 3]
[6, 5]

则其合并过程如下：

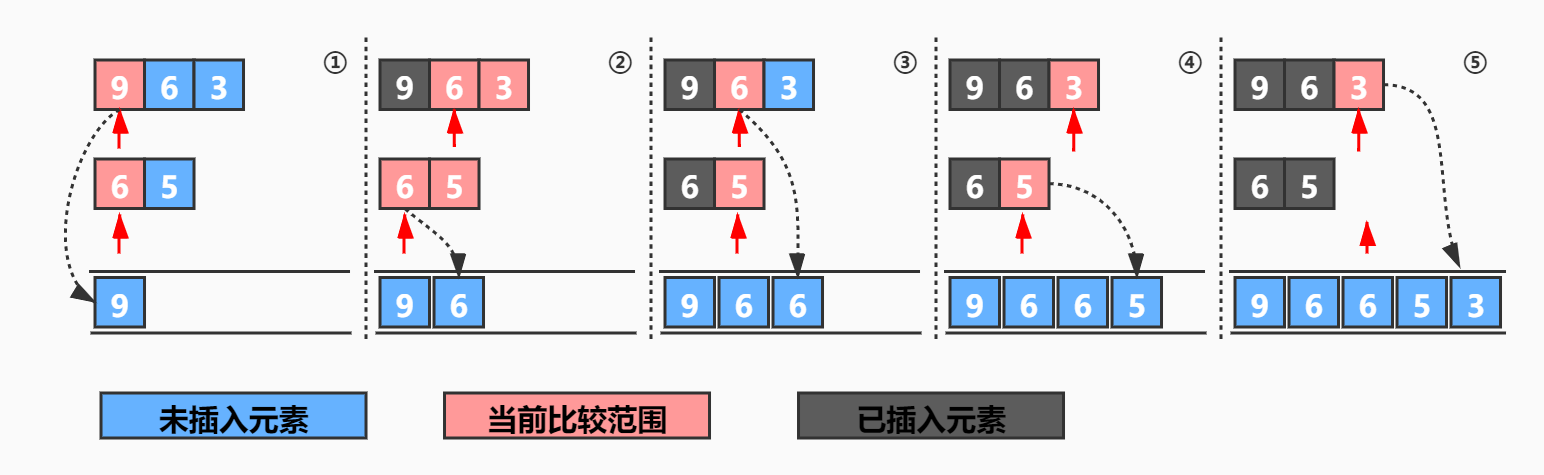
即：

• 若当前数字不同，则保留较大数字即可；
• 若当前数字不同，则保留后邻数字较大者（若后邻数字仍相同则继续向后比较）。

然后即可得到如下代码：

class Solution {
    public int[] maxNumber(int[] nums1, int[] nums2, int k) {
        int m = nums1.length, n = nums2.length;
        int[] res = new int[k];
        // minLen/maxLen：nums1中取的最短/长子序列长度
        int minLen = Math.max(0, k - n), maxLen = Math.min(k, m);
        for (int i = minLen; i <= maxLen; i++) {
            int[] subsequence1 = maxSubsequence(nums1, i);
            int[] subsequence2 = maxSubsequence(nums2, k - i);
            int[] curRes = merge(subsequence1, subsequence2);
            if (compare(curRes, 0, res, 0) > 0) {
                System.arraycopy(curRes, 0, res, 0, k);
            }
        }
        return res;
    }

    /**
     * 对 nums 保留 k 个数取最大子序列
     * @param nums
     * @param k
     * @return
     */
    private int[] maxSubsequence(int[] nums, int k) {
        int[] res = new int[k];
        // 要从数组中去除的元素数
        int remain = nums.length - k;

        Deque<Integer> deque = new LinkedList<>();
        for (int n : nums) {
            while (!deque.isEmpty() && remain > 0 && deque.peekLast() < n) {
                deque.pollLast();
                remain--;
            }
            deque.offerLast(n);
        }
        while (remain > 0) {
            deque.pollLast();
            remain--;
        }

        // 从单调递减栈中依次取出元素得到结果数组
        int idx = 0;
        while (!deque.isEmpty()) {
            res[idx++] = deque.pollFirst();
        }
        return res;
    }

    /**
     * 合并两个数组的最大子序列得到全局最大子序列
     * @param sequence1
     * @param sequence2
     * @return
     */
    private int[] merge(int[] sequence1, int[] sequence2) {
        int m = sequence1.length, n = sequence2.length;
        if (m == 0) {
            return sequence2;
        }
        if (n == 0) {
            return sequence1;
        }

        int[] res = new int[m + n];
        int idx1 = 0, idx2 = 0;

        for (int i = 0; i < (m + n); i++) {
            if (compare(sequence1, idx1, sequence2, idx2) > 0) {
                res[i] = sequence1[idx1++];
            } else {
                res[i] = sequence2[idx2++];
            }
        }

        return res;
    }

    /**
     * 比较 x 从 idx1 索引到结尾的子数组
     *   与 y 从 idx2 索引到结尾的子数组的大小
     * 如：
     *   x = [4, 6, 7, 2] , y = [4, 6, 7], 则 x > y;
     *   x = [4, 5, 7], y = [4, 6, 7], 则 x < y...
     * @param x
     * @param idx1
     * @param y
     * @param idx2
     * @return
     */
    private int compare(int[] x, int idx1, int[] y, int idx2) {
        int m = x.length, n = y.length;
        while (idx1 < m && idx2 < n) {
            int diff = x[idx1] - y[idx2];
            if (diff != 0) {
                return diff;
            }
            idx1++;
            idx2++;
        }
        if (idx1 == m && idx1 == n) {
            return 0;
        } else if (idx1 == m){
            return -1;
        } else {
            return 1;
        }
    }
}