强化学习导论 -章6 时序差分

时序差分学习

在开始时序差分的介绍执勤啊，我们需要知道为什么会有时序差分这种概念，我们前面学习到的主要的的内容，一个叫做贝尔曼方程，一个叫做动态规划，一个叫做蒙特卡洛，前两个需要对模型了解，知道发生的状态转移的概率和收益，第二个需每次从结束状态的反推从而获取到整条路径上的所有的更新。所以有没有一种方法，可以整合他们的优点，而且不需要他们的那么多限制

1. TD学习简介

1.1 基本思想

时序差分（TD）学习结合了蒙特卡洛（MC）方法和动态规划（DP）的优点：

• 像MC一样，可以直接从经验中学习，无需环境模型
• 像DP一样，基于已有估计进行更新，无需等待回合结束

2. TD(0)预测

2.1 TD预测的核心思想

TD(0)是最简单的TD算法，用于评估固定策略π。其核心是TD误差，为什么是这个公式我们将会下一节和MC对比的时候指出

$TDError={\delta }_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t)$

更新规则：
$V(S_t)\leftarrow V(S_t)+\alpha [R_{t+1}+\gamma V(S_{t+1})-V(S_t)]$

其中：

• $V(S_t)$：当前状态的价值估计
• $R_{t+1}$：即时奖励
• $\gamma V(S_{t+1})$：折扣后的下一状态价值估计
• $\alpha$：学习率

2.2 与MC方法的对比

MC更新，基于实际获取的$G_t$,然后更新$S_t$其中
$V_{\pi }(s)=E[G_t|S_t=s]$，所以更新规则是 $V(S_t)\leftarrow V(S_t)+[G_t-V(S_t)]$
但是继续展开那么就会得到
$$V_{\pi }(s)=E[G_t|S_t=s]=E[R_{t+1}+\gamma G_{t+1}]=E[R_{t+1}+\gamma V_{\pi }{S}_{t+1}]$$
显然这样的展开是一个期望一致的展开，TD(0)就是使用了这个期望值，我们基于当前的回报和剩下的回报来期望，而且下一个期望的值正好是下一个状态的价值函数，得到我们前面的更新公式

$$V(S_t)\leftarrow V(S_t)+\alpha [R_{t+1}+\gamma V(S_{t+1})-V(S_t)]$$
需要说明的是，学习率是一个超参，我们需要手动去配置他们

主要区别：

• MC使用实际回报$G_t$
• TD使用估计回报$R_{t+1}+\gamma V(S_{t+1})$
• TD可以在线学习，MC必须等待回合结束

2.3 TD(0)算法伪代码

初始化V(s)（对所有s∈S）
对于每个回合：
    初始化S
    对于回合中的每一步：
        A ← 根据策略π选择动作
        执行动作A，观察R, S'
        V(S) ← V(S) + α[R + γV(S') - V(S)]
        S ← S'
    直到S是终止状态

2.3 蒙特卡洛误差的差分形式

$G_t-V(s)=R_{t+1}+\gamma G_{t+1}-V(S_t)+\gamma V(S_{t+1})-\gamma V(S_{t+1})$
$={\delta }_t+\gamma (G_{t+1}-V(S_{t+1}))$
$...$
$={\sum }_{k=t}^{T-1}{\gamma }^{k-t}{\delta }_k$

3. TD优势和特点

3.1 TD的优势

1. 在线学习：每步都可以更新
2. 适用于连续任务
3. 利用马尔可夫性质
4. 通常比MC更高效

3.2 理论保证

• 在适当条件下，TD(0)收敛到真实值函数
• 学习率满足随机近似条件：
  • ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$
  • ${\sum }_{n=1}^{\infty }{\alpha }_n^2<\infty$

3.3随机游走

随机游走的例子我一开始使用了$ϵ$-贪婪的策略，导致一直没有学习到正确的曲线，原文中使用的是完全随机游走，然后得到的价值函数对比，我这里对每一个alpha，运行100次，每次1000幕，然后统计平均的价值价值函数，得到的图如下

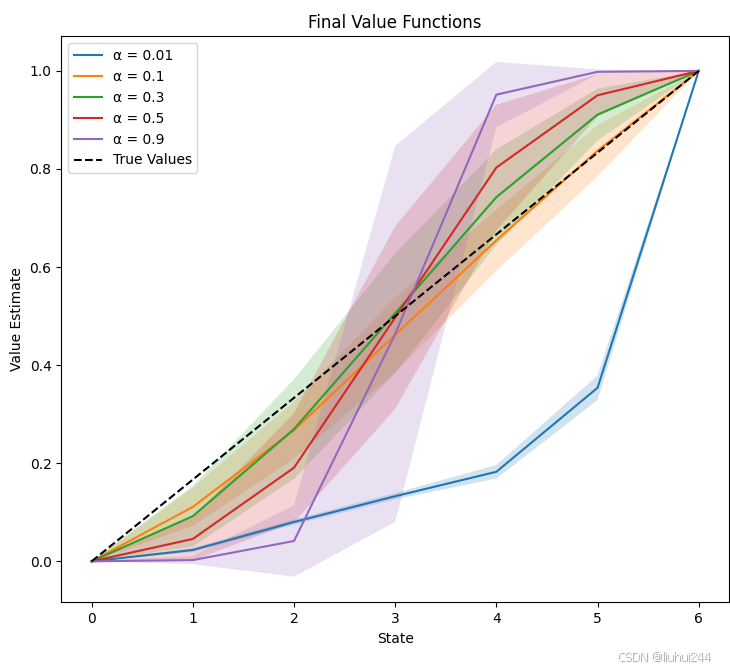
3.4 TD(0)的最优

这里有一个非常重要的概念需要引入，对比蒙特卡洛事件的回报，蒙特卡洛学习的是最小化训练集的最小RMS的过程，但是TD学习的是，使得最似然的MDP模型的参数，换句话表达，蒙特卡洛想要让自己的模型能够满足最小的误差结果，但是TD学习希望让自己的模型更加可能产生这个结果的序列，希望都能理解到这个核心的差异

4. Sarsa：同策略TD控制

什么是Sarsa, 就是State , action , reward , state(new), action(new)，所以你懂了吗？这里需要注意的是，我们
Sarsa扩展TD(0)来学习动作价值函数Q(s,a)。名称来自更新使用的元组：(S,A,R,S’,A’)。
需要注意的是，sarsa显然使用了下一个状态的action，所以这里是一个同轨策略。

4.2 更新规则

$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)]$

4.3 Sarsa算法伪代码

初始化Q(s,a)（对所有s∈S，a∈A）
对于每个回合：
    初始化S
    选择A从S使用从Q派生的策略
    对于回合中的每一步：
        执行动作A，观察R, S'
        选择A'从S'使用从Q派生的策略
        Q(S,A) ← Q(S,A) + α[R + γQ(S',A') - Q(S,A)]
        S ← S'
        A ← A'
    直到S是终止状态

4.4 有风的世界

原文中的例子，我经过了实际的测试，发现在epsilon = 0.1的时候，几乎很难学习完毕前面10个幕，因为目标太远了，TD(0)很难学习到目标的函数，基本都在随机测试，导致学习的事件特别的夸张，我自己的数学计算如下，因为最优解大概在15步左右，那么随机过去的概率是（1/0.1)^15次方，但是考虑到每一步都是-1的reward，理论上更应该推进agent去选择哪些尚未到达的状态,但是实际好像有异常

经过debug,我终于找到了bug的原因了，我在代码的q-table初始化的时候，一开始使用了如下的方法，为了节省资源

self.q = defaultdict(lambda: defaultdict(lambda: 0))

这个会在访问到特定的state_action的时候才会创建原始值0，但是在argmax的选取动作的情况下，并不会考虑那些没有出现过的情况，所以一直在之前探索过的情况下循环
我修改了代码

self.q = defaultdict(lambda: np.zeros(n_actions))        

任意一个state我们将会自动创建n_action元素，那么我们就可以达到我们想要的优先探索没有采取过的步骤的效果了，这个点很真实，希望大家能从我的失败里面学习到一些初始化的原则和方法。

但是我的还是学习的比较慢，需要500幕才能正确的学习到17步左右

Episode 10, Average steps: 203.00
Episode 20, Average steps: 73.80
Episode 30, Average steps: 61.20
Episode 40, Average steps: 66.80
Episode 50, Average steps: 47.80
Episode 60, Average steps: 48.60
Episode 70, Average steps: 37.60
Episode 80, Average steps: 29.60
Episode 90, Average steps: 31.20
Episode 100, Average steps: 27.10
Episode 110, Average steps: 26.70
Episode 120, Average steps: 22.00
Episode 130, Average steps: 20.70
Episode 140, Average steps: 28.10
Episode 150, Average steps: 25.20
Episode 160, Average steps: 19.70
Episode 170, Average steps: 22.90
Episode 180, Average steps: 23.30

5. Q-learning：离策略TD控制

如同前面我们说到的最关键的地方，sarsa是需要下一个s的action的，所以是一个同轨的策略，但是Q-learning不是。其中最核心的地方我们需要对比下q-learning和sarsa的更新差别。

Q-learn的更新函数
$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma {\max }_{a}Q(S_{t+1},a)-Q(S_t,A_t)]$
sarsa的更新函数
$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)]$

5.1.1 核心特点

• 行为策略（用于选择动作）和目标策略（用于更新）可以不同
• 直接估计最优动作值函数，不需要策略评估
• 可以使用任何探索策略（如ε-贪婪）

5.1.2 有风的世界–Q-learning

直接修改learn函数，使用q-learning的机制来进行更新得到的学习的轨迹

Episode 10, Average steps: 214.50
Episode 20, Average steps: 60.10
Episode 30, Average steps: 56.10
Episode 40, Average steps: 60.90
Episode 50, Average steps: 49.60
Episode 60, Average steps: 37.50
Episode 70, Average steps: 35.40
Episode 80, Average steps: 38.00
Episode 90, Average steps: 28.30
Episode 100, Average steps: 25.40
Episode 110, Average steps: 24.40
Episode 120, Average steps: 21.70
Episode 130, Average steps: 18.40
Episode 140, Average steps: 17.70
Episode 150, Average steps: 18.30
Episode 160, Average steps: 18.80
Episode 170, Average steps: 17.40
Episode 180, Average steps: 18.10
Episode 190, Average steps: 16.90
Episode 200, Average steps: 18.00

给出和sarsa的学习曲线对比，显然Q-learn具有学习的更快的优势，但是方差肯定也比较大，导致学习的曲线波动比sarsa更大

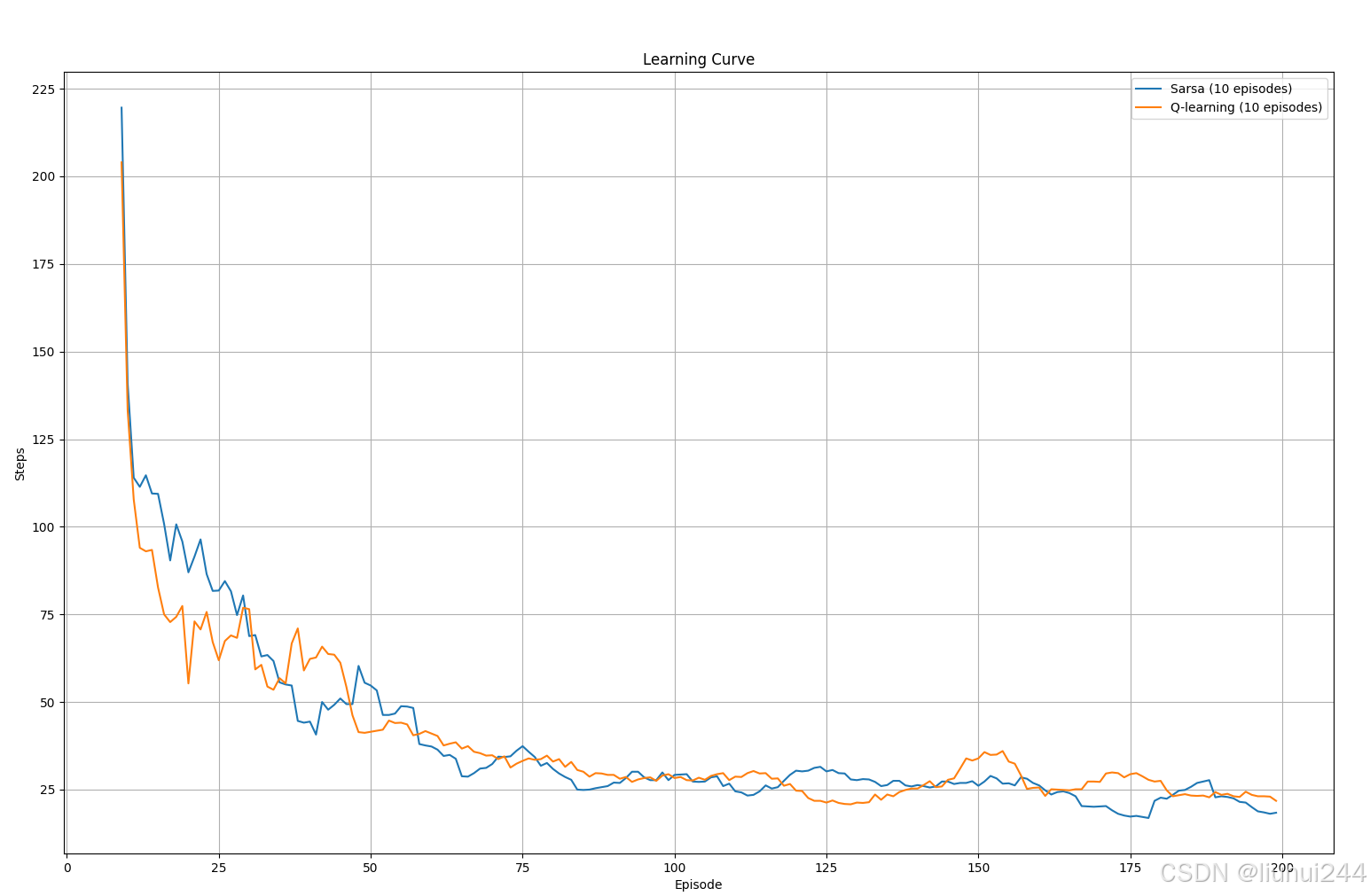
5.2 更新规则

$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma {\max }_{a}Q(S_{t+1},a)-Q(S_t,A_t)]$

关键区别：

• Sarsa使用实际选择的下一个动作$A_{t+1}$
• Q-learning使用最大值${\max }_{a}Q(S_{t+1},a)$

5.3 Q-learning算法伪代码

初始化Q(s,a)（对所有s∈S，a∈A）
对于每个回合：
    初始化S
    对于回合中的每一步：
        从S中使用策略（如ε-贪婪）选择A
        执行动作A，观察R, S'
        Q(S,A) ← Q(S,A) + α[R + γmax_a Q(S',a) - Q(S,A)]
        S ← S'
    直到S是终止状态

6. 期望Sarsa

6.1 基本思想

期望Sarsa是Sarsa的变体，使用下一状态所有动作的期望值而不是单个样本。

6.2 更新规则

$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma {\sum }_a\pi (a|S_{t+1})Q(S_{t+1},a)-Q(S_t,A_t)]$

其中$\pi (a|S_{t+1})$是目标策略下选择动作a的概率。

6.3 与Q-learning的关系

• Q-learning是期望Sarsa的特例
• 当目标策略是贪婪策略时：
  ${\sum }_a\pi (a|S_{t+1})Q(S_{t+1},a)={\max }_{a}Q(S_{t+1},a)$

6.4 有风的世界

增加了期望的sarsa的版本，长期来看期望sarsa有更稳定的学习曲线

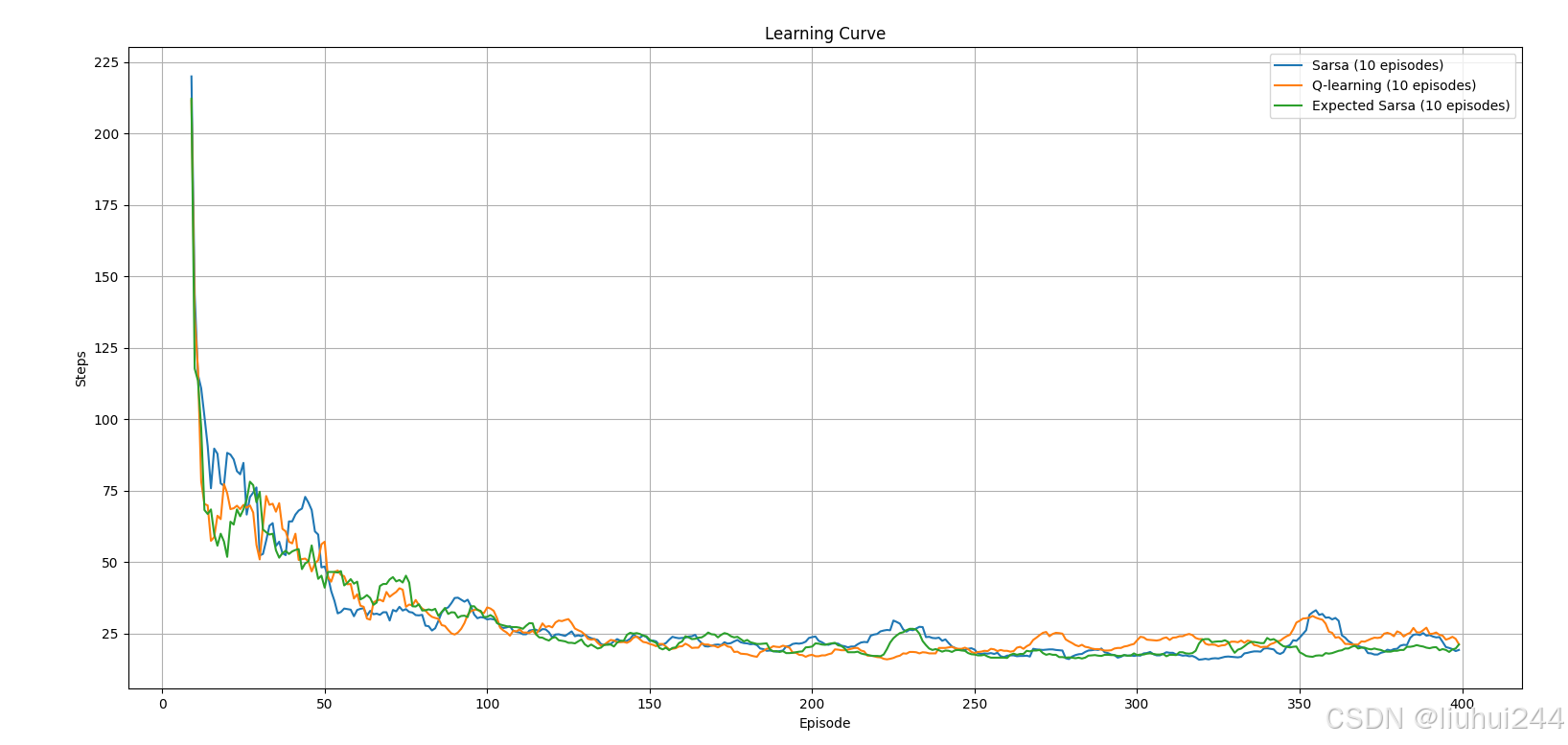
7. 算法对比

7.1 三种算法的特点对比

算法	类型	更新目标	特点
Sarsa	同策略	$Q(S_{t+1},A_{t+1})$	更保守，考虑探索风险
Q-learning	离策略	${\max }_{a}Q(S_{t+1},a)$	更激进，直接学习最优
期望Sarsa	可同可离	$\sum_a π(a	S_{t+1})Q(S_{t+1},a)$

7.2 选择建议

1. 安全性要求高：选择Sarsa
2. 希望学习最优策略：选择Q-learning
3. 计算资源充足，要求稳定：选择期望Sarsa

8. 最大化偏差和双重学习

8.1 最大化偏差问题

Q-learning和其他使用最大化操作的方法可能会出现过度乐观的估计：

• 原因：总是选择最大值会导致噪声产生正偏差
• 影响：可能导致次优策略

例如如果一个N(-0.1,1)的正太回报，如果第一次获取的reward很大，正好大于0.5，那么将会发现Q-learning会一直去选择这个期望值不高的函数，因为Q使用的乐观估计。为了减少方差，我们使用了double-Q，

8.2 双重Q-learning

解决方案是使用两个独立的价值函数：每次随机从两个Q值中选择一个来进行跟新，每次get_action也是随机从两个Q中来获取一个argmax的动作价值

1. 一个用于选择最优动作
2. 另一个用于评估该动作

更新规则：

0.5随机选择更新QA或QB
如果更新QA：
    QA(S,A) ← QA(S,A) + α[R + γQB(S',argmax_a QA(S',a)) - QA(S,A)]
如果更新QB：
    QB(S,A) ← QB(S,A) + α[R + γQA(S',argmax_a QB(S',a)) - QB(S,A)]

看起来有点拗口，但是实际上从A选择最大的动作a,但是使用B的Q值来判断Q值，这样

9. 实现考虑

9.1 参数选择

• 学习率α：通常从小值开始（如0.1）
• 探索率ε：从大值开始，逐渐减小
• 折扣因子γ：问题相关，通常0.9到0.99

9.2 实践建议

1. 初始值选择：建议乐观初始化
2. 探索策略：ε-贪婪是简单有效的选择
3. 步长设置：考虑使用衰减的学习率
4. 经验重放：考虑使用经验回放提高样本效率