强化学习导论 -章7 n步自举法

n步自举法：统一TD和MC方法

1. n步方法的基本思想

前面介绍了TD(0)的方法，好处是可以立马学习，坏处是只能学习到当前以后的一步，就像前面介绍的有风的世界的例子，显然前面需要很多步骤才能到达目的地，但是一幕只能学习到一个正向的反馈的值，如果这个时候可以学习到多步，则有可能在一个幕里面更新到多个前向的路径，从而学习的更快

1.1 引言

在前面我们学习了两种极端方法：

• TD(0)：只使用1步回报进行更新
• MC：使用完整回报进行更新

n步方法提供了这两种极端之间的中间选择。

1.2 n步回报定义

n步回报是从当前时刻开始，往后看n步的回报，然后用第n步状态的价值估计来自举，如同我们前面说的$G_t$的期望的展开，如果我们继续展开n步就可以得到下面的值，我们使用了V函数来代替了剩余的价值函数：

$G_{t:t+n}=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+{\gamma }^{n-1}{R}_{t+n}+{\gamma }^{n}V(S_{t+n})$

特殊情况：

• 当n=1时，就是TD(0)的回报: $G_{t:t+1}=R_{t+1}+\gamma V(S_{t+1})$
• 当n=∞时，就是MC的回报: $G_{t:\infty }=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...$

2. n步预测算法

原文里面一直在计算公式，但是很少举实际的例子，导致看的时候很难懂，像是在做数学题。
我这里举一个例子，比如n = 4，然后t = 0 ，那么就会在第4步，到达一个新的状态$s_4$，假设前面三步的回报都是0，第四步的回报是4，那么s0就会学习到一个不为0的回报，4*${\gamma }^3$,但是如果是TD(0)，第0步则不会学习到任何回报（因为前面的回报是0）

2.1 n步TD预测

更新规则，这里看起来会让人有误解好像同一个$S_t$每一步都在更新，但是实际上，都很上一次更新的这个状态的V值函数是一模一样的
$V_{t+n}(S_t)\leftarrow V_{t+n-1}(S_t)+\alpha [G_{t:t+n}-V_{t+n-1}(S_t)]$

2.2 n步TD算法伪代码

我真的不喜欢原文的代码的表达的形式，他的更新里面t表示的初始状态，但是在伪代码里面t是最后的状态，真的让人逻辑不是很通顺。
我这里用通俗易懂的话讲解一下这个逻辑，env一直正常的采样，我们要更新n步之前起始状态的值，那么就$\tau =t-(n-1)$，如果起始状态已经存在>= 0，那么获取n步$G_t$，更新起始状态的价值函数。如果最后的位置已经达到结束，则直接使用最后的回报代替所有的剩余价值函数。

初始化V(s)（对所有s∈S）
参数：步长α∈(0,1]，正整数n
所有存储和访问操作都按回合索引t取模n
对每个回合：
    初始化并存储S0
    T ← ∞
    对t = 0,1,2,...：
        如果t < T：
            执行At，观察Rt+1和St+1
            如果St+1是终止状态：T ← t+1
        τ ← t-n+1  # τ是要被更新的状态的时间
        如果τ ≥ 0：
            G ← 计算n步回报G_{τ:min(τ+n,T)}
            V(Sτ) ← V(Sτ) + α[G - V(Sτ)]
        直到τ = T-1

原文中的对于n步的差分形式并没有好好的的给出，我这边只能自己推导的形式只能是和TD(0）的一模一样才能推导的下去
${\delta }_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t)$
另一个推导是这样
$G_{t:t+n}=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+{\gamma }^{n-1}{R}_{t+n}+{\gamma }^{n}V(S_{t+n})$
$$=R_{t+1}+\gamma [R_{t+2}+...{\gamma }^{n-2}+r^{n-1}V(S_{t+n})]$$
$$=R_{t+1}+\gamma G_{t+1:t+n}$$

所以得到的推理形式，我这里不知道为什么只能推导n步，感觉不太对，有没有懂的人告知一下
$G_{t:t+n}-V(s)={\delta }_t+\gamma {\delta }_{t+1}+...$

3. n步Sarsa

3.1 n步Sarsa回报定义

扩展到动作价值：依然注意，这里的最后的动作是on-policy的

$G_{t:t+n}=R_{t+1}+\gamma R_{t+2}+...+{\gamma }^{n-1}{R}_{t+n}+{\gamma }^{n}Q(S_{t+n},A_{t+n})$

3.2 更新规则

$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [G_{t:t+n}-Q(S_t,A_t)]$

3.3 n步Sarsa算法伪代码

初始化Q(s,a)（对所有s∈S，a∈A）
参数：步长α∈(0,1]，小ε>0，正整数n
所有存储和访问操作都按回合索引t取模n
对每个回合：
    初始化并存储S0
    选择并存储A0
    T ← ∞
    对t = 0,1,2,...：
        如果t < T：
            执行At，观察Rt+1和St+1
            如果St+1是终止状态：
                T ← t+1
            否则：
                选择At+1（例如使用ε-贪婪）
        τ ← t-n+1
        如果τ ≥ 0：
            G ← 计算n步回报G_{τ:min(τ+n,T)}
            Q(Sτ,Aτ) ← Q(Sτ,Aτ) + α[G - Q(Sτ,Aτ)]
        直到τ = T-1

3.4 悬崖散步

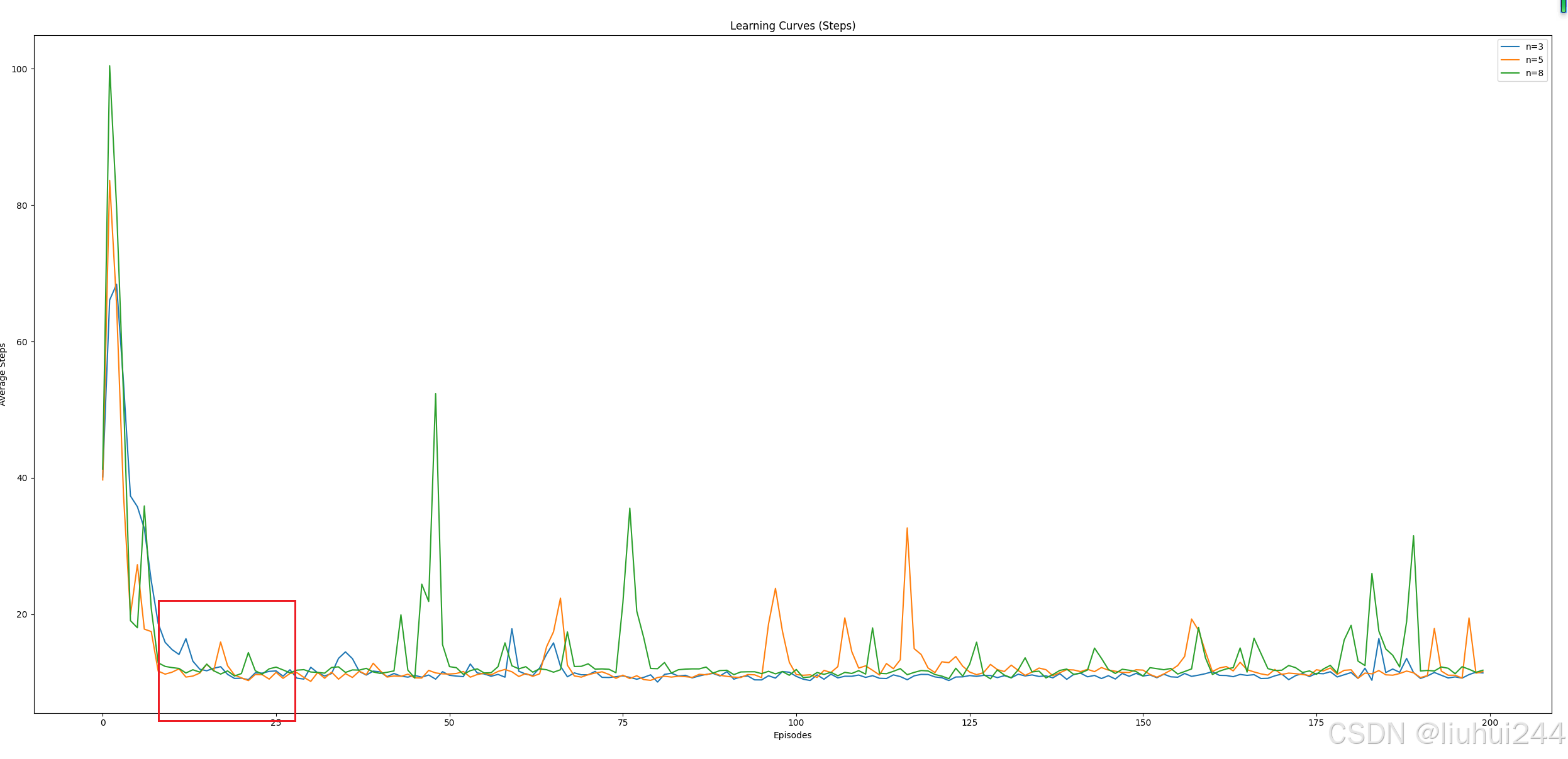
这里使用了不同的n的平均步数的下降的情况，可以看到不同的n值可以在不同的步骤上
手搓代码踩了很多坑，得到的了如下的图标的学习曲线

• 比如最好到了Done以后注意要把memory里面的所有的步骤都更新完毕，否则最后的几步总是得不到
• 更新注意使用小的alpha，否则会导致最后的学习函数波动的非常明显
• 注意对比reward和steps的值，否则可能导致步数下降，但是实际reward并没有增加
  

4. n步离策略学习

4.1 重要度采样比率

离策略情况下需要使用重要度采样比率来纠正：
对于每一步，我们要都将选择这个动作和经验一起存放在一个数组里面,这样就可以顺利的关于重要度采样的prod信息了

${\rho }_{t:h}={\prod }_{k=t}^{min(h,T-1)}\frac{\pi (A_k|S_k)}{b(A_k|S_k)}$

其中：

• π是目标策略
• b是行为策略

4.2 n步离策略更新

带重要度采样的n步回报：

$V(S_t)\leftarrow V(S_t)+\alpha [{\rho }_{t:t+n-1}(G_{t:t+n}-V(S_t))]$
显然，这个问题和之前的一样，存在一个方差无穷的问题，所以后面有一些别的方法，可以减少重要度采样带来的方差的扩散的问题

5. 没有重要度采样的离策略方法：n步树回溯算法

记得我们上一章节提到的期望Sarsa，当时我们就提到这是一个离轨采样的算法，因为他只用到了当前的s，a没有下一步的a，下一步的a，我们通过期望的形式来获取到了所有的action的权重和收益。同理，如果我们将其发散到N步，得到的n步树回溯法

5.1 基本思想可能那就

不使用重要度采样，而是考虑所有可能的动作及其概率。

5.2 树备份n步回报

回顾我们的单步期望Sarsa的回报形式
$$G_t=R_{t+1}+\gamma \sum _a\pi (a|S_{t+1})Q(S_{t+1},a)(7.15)$$
原文中的表达形式没问题，但是展开的过程并没有做过多的解释，我做了一个逻辑上的说明，希望大家都能理解的记住这个表达的真正的含义和意思
其实很简单，对于(7.15)在n步发生的不同的事情，就是我们知道了有一个动作是已经实际发生了，所以我们将其拆开来看
$$G_t=R_{t+1}+\gamma (\sum _{a\ne A_{t+1}}\pi (a|S_{t+1})Q(S_{t+1},a)+\pi (A_{t+1}|S_{t+1})G_{t+1})(7.15)$$
既然我们知道了G的表达形式，那么展开$G_{t+1}$就可以得到我们一般的表达形式，不过我有点不敢展开，总的来说就是$G_{t:t+n}=R的回报+期望动作的回报+剩余的Q函数回报$
R的回报是对每一个R进行$\gamma$和动作选择的概率加权后的回报，
${\sum }_{h=t+1}^{t+n}{R}_h\ast {\gamma }^{h-(t+1)}\ast {\prod }_{t+2}^h\pi (A_{h-1}|S_{h-1})$

5.3 更新规则

更新规则是和其他的基本一致
$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [G_{t:t+n}-Q(S_t,A_t)]$
伪代码中的也是和之前的蒙特卡洛的算法一致，从结束状态然后倒着推进，直到起始时间

$\lambda$

5.4 n步Q( $\sigma$ )的算法

这个算法主要是综合了n步 Q算法和期望算法，我这里不作为展开了，因为没有一个特定的要选择这个函数的场景，具体的做法涉及到一个随机算子$\sigma$，随机选择是否使用maxQ还是使用期望的树回溯，

6. n步方法的优势和缺点

6.1 优势

1. 提供TD和MC之间的平滑过渡
2. 可以权衡偏差和方差
3. 通常比单步TD和纯MC表现更好

6.2 缺点

1. 计算复杂度随n增加
2. 需要更多内存存储n步历史
3. n的选择需要调优