leecode79. 单词搜索

最新推荐文章于 2025-11-25 12:11:25 发布

原创最新推荐文章于 2025-11-25 12:11:25 发布 · 264 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#java #jvm #数据库

本文介绍如何使用回溯法解决在给定的 mxn 字符网格中查找是否存在指定单词的问题，通过实例演示了如何遍历网格并利用回溯技巧避免重复路径。

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

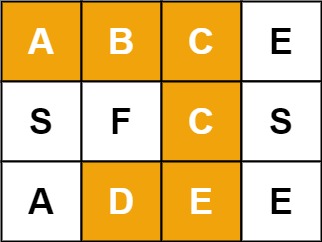
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true
示例 2：

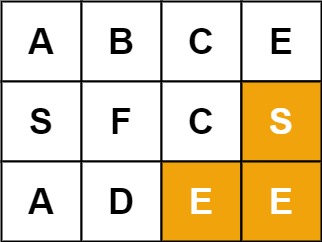
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true
示例 3：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

使用回溯大法：

class Solution {
    public boolean exist(char[][] board, String word) {
        //遍历board
        for (int start = 0; start < board.length; start++) {
            for (int end = 0; end < board[start].length; end++) {
                //当前点开始比较
                if (dfs(board, start, end, word, 0)) {
                  
                    return true;
                }
            }
        }
        return false;

    }

    public boolean dfs(char[][] board, int start, int end, String word, int index) {
        //字符比较完毕
        if (index >= word.length()) {
            return true;
        }
        boolean flag = false;
        //检查当前点是否正确
        if (check(board, start, end, word, index)) {
            char tmp = board[start][end];
            //设置为访问过
            board[start][end] = 3;
            //右边不能通过
            if (!dfs(board, start + 1, end, word, index + 1)) {
                //左边不能通过
                if (!dfs(board, start - 1, end, word, index + 1)) {
                    //下边不能通过
                    if (!dfs(board, start, end - 1, word, index + 1)) {
                        //上边
                        flag = dfs(board, start, end + 1, word, index + 1);
                    } else {
                        flag = true;
                    }
                } else {
                    flag = true;
                }
            } else {
                flag = true;
            }
            //还原现场
            board[start][end] = tmp;
            return flag;
        }
        return false;
    }

    public boolean check(char[][] grid, int start, int end, String word, int index) {
        if (start < 0 || start >= grid.length || end < 0 || end >= grid[0].length) {
            return false;
        }

        if (grid[start][end] == 3) {
            return false;
        }
        return grid[start][end] == word.charAt(index);
    }
}