遗传算法及其实现

原创已于 2024-11-08 17:10:03 修改 · 3.4k 阅读

17 ·

CC 4.0 BY-SA版权

文章标签：

#遗传算法 #优化算法

于 2017-05-19 10:45:38 首次发布

机器学习同时被 3 个专栏收录

43 篇文章

订阅专栏

python

21 篇文章

订阅专栏

模拟及优化算法

5 篇文章

订阅专栏

遗传算法是一种基于生物进化理论的优化搜索算法，通过模拟选择、交叉、突变等过程来寻找问题的最优解。文章介绍了遗传算法的基本思想，包括编码与解码、选择策略、交叉操作和基因突变，并提供了Python实现的简介。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

点击下方图片查看HappyChart专业绘图软件

遗传算法是计算数学中用于解决最优化的搜索算法，是进化算法的一种。它是借鉴了生物进化学中的一些现象而发展起来的，这些现象包括遗传，突变，自然选择以及杂交等。

遗传算法的思想

遗传算法是模拟生物学种的进化论，物种朝着有利于自己的方向发展，这在遗传算法中表现为朝着最优化的方向发展。在进化过程中，遗传算法模拟基因的行为，首先选择有优势的基因，并对基因进行配对，然后等位基因进行交换，并有一定的概率进行基因变异，这就导致了下一代基因的产生，产生新的个体。

编码和解码

遗传算法的编码有两种，二进制编码和浮点数编码。将一个二进制串(长度为n)转化为区间[a,b]里对应是实数值：
（1）将一个二进制串代表的二进制转化为10进制数
$(b_0\cdots b_{n-2}b_{n-1})_2=(\Sigma_{i=0}^{n-1}b_i\cdot 2^i)_{10}=x^t$
（2）对应区间内的实数
$a+x^t\frac{b-a}{2^{n}-1}$

选择

越适应的个体越有可能繁衍后代，通过适应性函数（被选中的概率函数）选择个体进行繁殖，某个个体被选中的概率为
$p_i = \frac{f_i}{\Sigma_{i=1}^nf_i}$

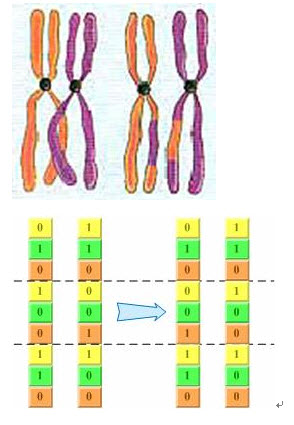
交叉

即同源染色体联会过程中，非姐妹染色单体之间发生交叉，并交换一部分染色体，也是等位基因的交换。
这里写图片描述

基因突变

基因突变是染色体某一个基因点的改变，基因串上0或1突变为1或0。例如
$1001000101110$
经过突变后可能变为
$1001000101111$

Python实现

# -*- coding:utf-8 -*-

#随机生成二进制编码
import random
def geneEncoding(pop_size, chrom_length):
    pop = [[]]
    for i in range(pop_size):
        temp = []
        for j in range(chrom_length):
            temp.append(random.randint(0,1))
        pop.append(temp)
    return pop[1:]
# pop = geneEncoding(pop_size,chrom_length)

#对二进制编码进行解码并计算
import math
def decodechrom(pop, chrom_length):
    temp = []
    for i in range(len(pop)):
        t = 0
        for j in range(chrom_length):
            t += pop[i][j] * (math.pow(2,j)) #计算的对吗，上面应该range(chrom_lenth,0,-1)
        temp.append(t)
    return temp

def calobjValue(pop, chrom_length, max_value):
    temp1 = []
    obj_value = []
    temp1 = decodechrom(pop,chrom_length)
    for i in range(len(temp1)):
        x = temp1[i] * max_value / (math.pow(2, chrom_length)-1)
        obj_value.append(10*math.sin(5*x) + 7 * math.cos(4*x))
    return obj_value

#淘汰个体(去除负值)
def calfitValue(obj_value):
    fit_value = []
    c_min = 0
    for i in range(len(obj_value)):
        if (obj_value[i] + c_min > 0):
            temp = c_min + obj_value[i] #c_min可以没有
        else:
            temp = 0.0
        fit_value.append(temp)
    return fit_value

#选择
def sum(fit_value):
    total = 0
    for i in range(len(fit_value)):
        total += fit_value[i]
    return total

def cumsum(fit_value):
    for i in range(len(fit_value)-2,-1,-1):
        t = 0
        j = 0
        while j <= i:
            t += fit_value[j]
            j += 1
        fit_value[i] = t
        fit_value[len(fit_value)-1] = 1 #why set it to 1

def selection(pop, fit_value):
    newfit_value = []
    #适应度总和
    total_fit = sum(fit_value)
    for i in range(len(fit_value)):
        newfit_value.append(fit_value[i] / total_fit)
    #计算累计概率
    cumsum(newfit_value)
    ms = []
    pop_len = len(pop)
    for i in range(pop_len):
        ms.append(random.random())
    ms.sort()
    fitin = 0
    newin = 0
    newpop = pop
    #转轮盘选择法
    while newin < pop_len:
        if(ms[newin] < newfit_value[fitin]):
            newpop[newin] = pop[fitin]
            newin += 1
        else:
            fitin += 1
    pop = newpop

#交叉
def crossover(pop, pc):
    pop_len = len(pop)
    for i in range(pop_len - 1):
        if random.random() < pc:
            cpoint = random.randint(0,len(pop[0]))
            temp1 = []
            temp2 = []
            temp1.extend(pop[i][0:cpoint])
            temp1.extend(pop[i+1][cpoint:len(pop[i])])
            temp2.extend(pop[i+1][0:cpoint])
            temp2.extend(pop[i][cpoint:len(pop[i])])
            pop[i] = temp1
            pop[i+1] = temp2

#变异
def mutation(pop, pm):
    px = len(pop)
    py = len(pop[0])
    for i in range(px):
        if random.random() < pm:
            mpoint = random.randint(0,py-1)
            if(pop[i][mpoint] == 1):
                pop[i][mpoint] = 0
            else:
                pop[i][mpoint] = 1

#找出最优解和最优解的基因编码
def best(pop, fit_value):
    px = len(pop)
    best_individual = []
    best_fit = fit_value[0]
    for i in range(1,px):
        if fit_value[i] > best_fit:
            best_fit = fit_value[i]
            best_individual = pop[i]
    return [best_individual, best_fit]

#计算二进制序列代表的数值
def b2d(b, max_value, chrom_length):
    t = 0
    for j in range(len(b)):
        t += b[j] * math.pow(2,j)
    t = t * max_value / (math.pow(2, chrom_length) - 1)
    return t

import matplotlib.pyplot as plt

print 'y = 10 * math.sin(5*x) + 7 * math.cos(4*x)'


pop_size = 500  #种群数量
max_value = 10  #基因中允许出现的最大值
chrom_length = 10 #染色体长度
pc = 0.6        #交配概率
pm = 0.01       #变异概率
results = [[]]  #存储每一代的最优解，N个二元组
fit_value = []  #个体适应度
fit_mean = []   #平均适应度

pop = geneEncoding(pop_size, chrom_length)

for i in range(pop_size):
    obj_value = calobjValue(pop, chrom_length, max_value)
    fit_value = calfitValue(obj_value) #淘汰
    best_individual, best_fit = best(pop, fit_value)
    results.append([best_fit,b2d(best_individual,max_value,chrom_length)])
    selection(pop, fit_value) #新种群复制
    crossover(pop, pc) #交叉
    mutation(pop,pm) #变异

results = results[1:]
results.sort()

X = []
Y = []
for i in range(500):
    X.append(i)
    t = results[i][0]
    Y.append(t)

plt.plot(X,Y)
plt.show()

这里写图片描述