leetcode 42|407. Trapping Rain Water 1|2

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
For example, 
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

题目的意思就是：每一个数字代表一个树立的木块，合起来可以盛多少水

方法一：递归。
      1、找最高的那个，下标为i
      2、i的左右分别找最高
      3、往左右迭代

class Solution {
public:
    int findleft(vector<int>& height, int flag, int sum)
    {
        int ff;
        int max = 0;
        
        for (int i = 0; i < flag; i++)
        {
            if (height[i] > max)
            {
                max = height[i];
                ff = i;
            }
        }
            
        if (max == 0)
            return sum;
            
        for (int i = ff + 1; i < flag; i++)
            sum += height[ff] - height[i];
            
        sum = findleft(height, ff, sum);   
        return sum;
    }   
    
    int findright(vector<int>& height,int flag,int sum)
    {
        int ff;
        int max = 0;
        
        for(int i = flag + 1; i < height.size(); i++)
        {
            if (height[i] > max)
            {
                max = height[i];
                ff = i;
            }
        }
                 
        if (max == 0)
            return sum;
              
        for(int i = flag + 1; i < ff; i++)
            sum += height[ff] - height[i];
                
        sum = findright(height, ff, sum);
        return sum;
    }
    
    int trap(vector<int>& height) 
    {
        int max = 0;
        int flag = -1;
        for (int i = 0; i < height.size(); i++)
        {
            if (height[i] > max)
            {
                max = height[i];
                flag = i;
            } 
        }
        int sum = 0;
        sum = findleft(height, flag, sum);
        sum = findright(height, flag, sum);
        return sum; 
    }
};

方法二：


这道题的思路是采用l和r两个指针，维护装水两边的位置。

当l处高度低时，说明l右侧装的水肯定和l处一样高，此时逐步右移l，同是加上l处与右移后位置高度差（因为这里都能装水啊），直到再遇到同样高或者更高的位置。然后进行下一轮判断。

同样，当r处高度低时，说明r左侧的水肯定和r处一样高，此时逐步左移r，同是加上r处与左移后位置高度差，直到再遇到同样高或者更高的位置

最后直到l和r相遇，结束。

时间复杂度：O(n)

空间复杂度：O(1)

class Solution {
public:
    int trap(vector<int>& height) 
    {
        int n = height.size();
        int l = 0, r = n - 1, res = 0, minh;
        
        while (l < r)
        {
            minh = min(height[l],height[r]);
            if (height[l] == minh)
            {
                while(++l < r && height[l] < minh)
                {
                    res += minh - height[l];
                }
            }
            else
            {
                while (l < --r && height[r] < minh)
                {
                    res += minh - height[r];   
                }
            }
        }
        return res;
    }
};

407. Trapping Rain Water II

Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.

Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.

Example:

Given the following 3x6 height map:
[
  [1,4,3,1,3,2],
  [3,2,1,3,2,4],
  [2,3,3,2,3,1]
]

Return 4.

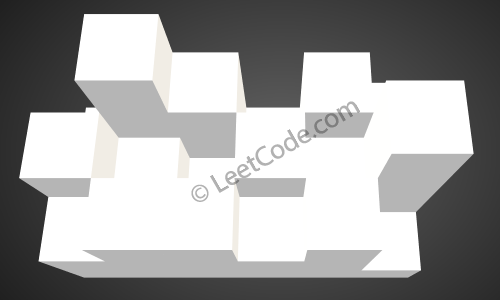
The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.

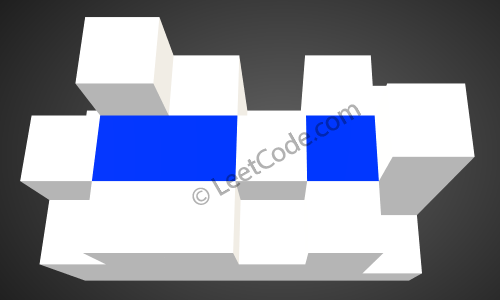
After the rain, water are trapped between the blocks. The total volume of water trapped is 4.

class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) 
    {   
        multimap<int, pair<int,int>> A; // 高度 和 位置
        int row = heightMap.size();
        if (row == 0) return 0;
        int col = heightMap[0].size();
        if (col == 0) return 0;
        
        vector<vector<bool>> flag(row, vector<bool>(col, false));
        for (int i = 0; i < row; i++)
        {
            for (int j = 0; j < col; j++)
            {
                if (i == 0 || j == 0 || i == row - 1 || j == col - 1) //先把边界存入。因为要从边界开始遍历
                {    
                    A.insert(make_pair(heightMap[i][j], make_pair(i, j)));
                    flag[i][j] = true;
                }
            }
        }
        
        int haiba = INT_MIN;
        int a[4] = {0, 1, 0, -1};
        int b[4] = {1, 0, -1, 0};
        int ret = 0;
        while (!A.empty())
        {
            auto it = A.begin();    //当前最矮 
            int h = it->first, x = it->second.first, y = it->second.second;
            A.erase(it);
            haiba = max(haiba, h);  //海拔 是在上升的
            
            for (int i = 0; i < 4; i++)
            {
                int _x = x + a[i], _y = y + b[i];
                if (!isvaild(_x, _y, row, col) || flag[_x][_y])
                    continue;
                flag[_x][_y] = true;
                if (heightMap[_x][_y] < haiba)  //比 能流出去的最低海拔矮 就能存水
                    ret += haiba - heightMap[_x][_y];
                A.insert(make_pair(heightMap[_x][_y], make_pair(_x, _y)));
            } 
        }
        return ret;
    }
    
    bool isvaild(int x, int y, int row, int col)
    {
        return x >= 0 && x < row && y >= 0 && y < col;
    } 
};