决策树模型类型及计算方法

决策树是一种基于树结构的机器学习模型，通过递归划分数据实现分类或回归。以下是几种核心决策树算法及其计算逻辑：

---

1. ID3 决策树（Iterative Dichotomiser 3）

• 用途：分类任务（不支持连续特征和回归）。

• 特征选择标准：信息增益（Information Gain）。

  • 信息熵：衡量数据集的混乱度。

    

    pi​ 为数据集中第 i类样本的比例。

  • 信息增益：选择分裂后熵减少最多的特征。

    

    V为特征 A 的取值数，Dv​ 是特征 A 取第 v 值的子集。

• 流程：

  1. 计算所有特征的信息增益。

  2. 选择增益最大的特征作为当前节点。

  3. 递归分裂子节点，直到纯度达标或无法分裂。

• 缺点：

  • 偏向取值多的特征（如“用户ID”）。

  • 无法处理连续特征和缺失值。

---

2. C4.5 决策树

• 改进点：解决ID3的不足，支持连续特征和缺失值。

• 特征选择标准：信息增益率（Gain Ratio）。

  • 固有值（Intrinsic Value）：惩罚多值特征。

    

  • 信息增益率：

    

• 处理连续特征：

  • 对连续值排序后，选择最佳分割点（如中位数）。

• 流程：

  1. 对每个特征计算增益率。

  2. 选择增益率最高的特征分裂。

  3. 递归生成子树，后剪枝防止过拟合。

---

3. CART 决策树（Classification and Regression Tree）

• 用途：分类和回归任务。

• 特征选择标准：

  • 分类任务：基尼指数（Gini Index）。

    

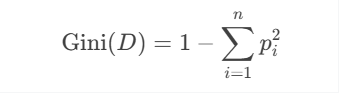
  • 回归任务：最小平方误差（MSE）。

    

    y^为节点样本的均值。

• 分裂方式：

  • 二叉树结构，每个节点仅分裂为左右两个子集。

  • 遍历所有特征及切分点，选择基尼指数或MSE最小的分裂方式。

• 剪枝方法：

  • 成本复杂度剪枝（CCP）：平衡树的复杂度与误差。

    

---

4. C5.0 决策树

• 改进点：C4.5的商业优化版本。

• 特点：

  • 更高的计算效率，支持更大数据集。

  • 自动处理缺失值，支持Boosting增强。

• 核心逻辑：与C4.5类似，但引入自适应增强（AdaBoost）提升精度。

---

模型对比与适用场景

算法	任务类型	特征选择标准	树结构	优点	缺点
ID3	分类	信息增益	多叉树	简单直观	无法处理连续特征，偏向多值特征
C4.5	分类	信息增益率	多叉树	支持连续特征，解决ID3偏向问题	计算复杂度高
CART	分类、回归	基尼指数、平方误差	二叉树	高效、支持回归任务	可能生成较深的树
C5.0	分类（增强版）	信息增益率	多叉树	高效、支持Boosting	商业闭源

---

关键计算示例

示例1：基尼指数计算（CART分类树）

假设数据集 DD 有10个样本，类别分布为 [7, 3]（正例:负例=7:3）：

若按某特征分裂后，子节点基尼指数分别为 0.3（左）和 0.4（右），样本数比例为 6:4：

加权基尼=0.3×610+0.4×410=0.34

选择基尼指数下降最大（0.42 - 0.34 = 0.08）的分裂点。

示例2：回归树MSE计算（CART回归树）

节点样本目标值为 [2, 4, 6]，均值为 y^=4：

---

总结

• ID3/C4.5：适合分类任务，C4.5优化了连续特征处理。

• CART：全能型，支持分类和回归，二叉树结构高效但需剪枝。

• 选择建议：

  • 需要可解释性 → CART（基尼指数）。

  • 高维数据 → C4.5/C5.0（信息增益率）。

  • 回归任务 → CART（MSE或MAE）。