1. 如何根据坐标架进行点的坐标变换 | |||||||
|
首先坐标架定义成 struct PNT3D{
double x,y,z;
};
struct FRAME{
PNT3D O, OX, OY, OZ;
};
假设有一个点 p 定义在 frame 所在坐标系 WC(World Coordinate) 之中,也就是说 p 在 frame 之外。为了将 p 转入 frame,我们首先需要作平移 p1 = p - frame.O; 这个时候 p1 相当于定义在一个将 WC 平移到 frame.O 的一个坐标架之中。这个坐标架和 frame.O 供用坐标原点,但是三个坐标轴并不一定相同。为了得到 frame 中的三个坐标分量我们只须将 p1 和三个基矢量作点积 WC->frame 变换公式: p2.x = p1*frame.OX = (p-frame.O)*frame.OX; p2.y = p1*frame.OY = (p-frame.O)*frame.OY; p2.z = p1*frame.OZ = (p-frame.O)*frame.OZ; 其中 * 代表点积。这里所得到的 p2 就是 WC 中的 p 在 frame 中对应的点。到此为止我们完成了电从坐标架之外变换到坐标架内。同样的,我们也可以采用简单的方法把点从坐标架内变换到坐标架之外。 假设 p 是 frame 之内的点,首先 p1 = p.x*frame.OX + p.y*frame.OY + p.z*frame.OZ; 上面的公式将 p 的各个分量作为权值将三个坐标架的基矢量累加起来,得到的 p1 相当于平移 WC 和 frame 重合坐标原点的坐标架中的点。接下来,自然是处理平移 frame->WC 变换公式: p2 = p1 + freame.O; = p.x*frame.OX + p.y*frame.OY + p.z*frame.OZ + frame.O;p2 就是转换到 WC 的点。 | |||||||
| |||||||
|
矩阵在图形程序中应用十分广泛。它可以表达更复杂的变换形式。这里所指的矩阵是左乘矩阵,即矩阵位于点的左边。
我们可以用一个矩阵来代表从坐标架外到坐标架中的变换,也可以用一个矩阵代表从坐标架之中到坐标架之外的变换。下面的 mat 是按照行优先规则存放的矩阵。从坐标架中变换到坐标架外 frame->WC 的矩阵如下 frame->WC 变换矩阵: mat[0] = OX.x; mat[1] = OY.x; mat[2] = OZ.x; mat[3] = Oc.x; mat[4] = OX.y; mat[5] = OY.y; mat[6] = OZ.y; mat[7] = Oc.y; mat[8] = OX.z; mat[9] = OY.z; mat[10] = OZ.z; mat[11] = Oc.z; mat[12] = 0; mat[13] = 0; mat[14] = 0; mat[15] = 1; 其中,OX, OY, OZ 是坐标架的三个基矢量,Oc 是坐标架的坐标原点。我们将这个矩阵乘以点 p(x,y,z,1) p1 = mat*p; 我们可以得到 p1 就是 WC 坐标系下面的点。下面是这个矩阵的推导过程,如果觉得头大,可以跳过去。
搞定了 frame->WC 的矩阵,我们现在来搞 WC->frame 的矩阵 WC->frame 变换矩阵: mat[0] = OX.x; mat[1] = OX.y; mat[2] = OX.z; mat[3] = -(Oc.x*OX.x + Oc.y*OX.y + Oc.z*OX.z); mat[4] = OY.x; mat[5] = OY.y; mat[6] = OY.z; mat[7] = -(Oc.x*OY.x + Oc.y*OY.y + Oc.z*OY.z); mat[8] = OZ.x; mat[9] = OZ.y; mat[10] = OZ.z; mat[11] = -(Oc.x*OZ.x + Oc.y*OZ.y + Oc.z*OZ.z); mat[12] = 0; mat[13] = 0; mat[14] = 0; mat[15] = 1; 写代码的时候把这一堆抄过去就行了。如果不想看推导,就跳过下面的部分。
| |||||||
|
这个最好办了。我们这里讨论的矩阵都是左乘矩阵,所以把矩阵乘以点就完成了变换。 x = M[0][0]*Px + M[0][1]*Py + M[0][2]*Pz + M[0][3]; y = M[1][0]*Px + M[1][1]*Py + M[1][2]*Pz + M[1][3]; z = M[2][0]*Px + M[2][1]*Py + M[2][2]*Pz + M[2][3]; 这里的 M 是一个 4*4 的二维数组,存放行优先的矩阵。 | |||||||
|
曲线、曲面方程有参数方程、非参数方程等形式。当然曲线、曲面还可能由微分方程描述。这个时候微分方程如果没有公式解,事情就很麻烦。计算机中一般比较容易处理参数方程。参数方程作变换形式上很简单
右边的结果会得到一个矢量,最终可以得到 (F1x, F1y, F1z) 的形式,这是一个新的参数方程。如果曲线曲面由非参数方程描述 F(x,y,z)=0,比如
这个时候,你可以尝试解出 x,y,z: 令 x = u,y = v,可以得到
这下得到参数方程了,可以按照前面讲的步骤作转换。最后你会得到曲线、曲面变换后的参数方程。接下来你可以尝试着消去这些中间参数 u,v。这个过程可能会比较艰难。 如果遇到隐式方程,无法解出,比如
这是最倒霉的情况,求解是没希望的。当然,如果你不要求精确的公式,你还是可以先令 x=u, y=v,代入之后,用泰勒展开求的 z 的级数,这也是一个方法哦:) | |||||||
如何根据坐标架进行点的坐标变换
最新推荐文章于 2022-05-16 02:18:09 发布
 本文深入探讨了在计算机图形学中如何利用坐标变换和矩阵进行点坐标变换,包括从坐标架内外变换的方法及推导过程,以及如何生成变换矩阵,并通过实例解释了如何使用矩阵进行点坐标变换。同时,介绍了曲线、曲面方程在不同坐标系间的变换方法,以及在实际应用中处理隐式方程的策略。
本文深入探讨了在计算机图形学中如何利用坐标变换和矩阵进行点坐标变换,包括从坐标架内外变换的方法及推导过程,以及如何生成变换矩阵,并通过实例解释了如何使用矩阵进行点坐标变换。同时,介绍了曲线、曲面方程在不同坐标系间的变换方法,以及在实际应用中处理隐式方程的策略。




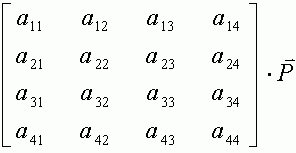

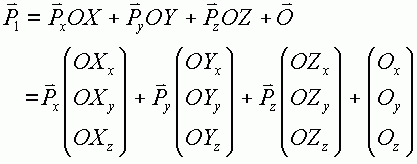
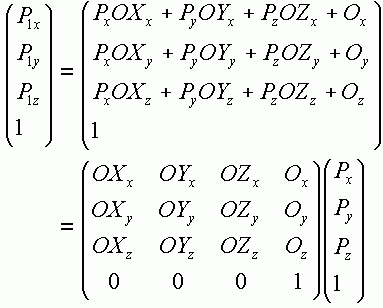
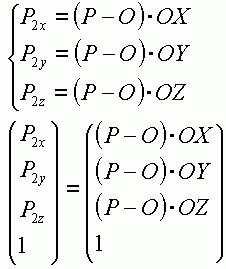
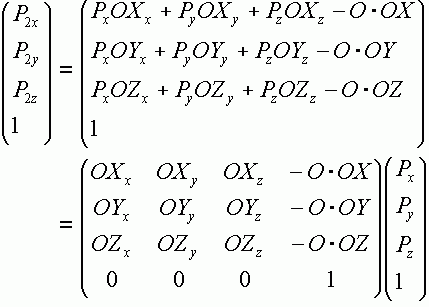
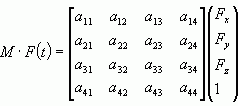
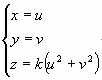
















 967
967

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








