数据结构 树笔记-1 树的定义与结构

树的结构

要熟悉树的结构，结构决定性质，性质决定用途

1.  树是一种树型的层次结构

2.  定义方式上看，树是一种递归的定义方式，因为每个结点均可以作为根结点生出孩子。

树的根只有一个，

但根结点可以有多个，只要有孩子结点，那么这个结点就是一个根结点，所以除了叶子结点的所有其余结点都 是一个根结点

3.  一（作为根结点的这个结点）对多（孩子）：

直接前驱——父亲结点

直接后继——孩子结点

树的根没有直接前驱，可以有多个直接后继；

叶子结点有一个直接前驱，没有直接后继；

除了根节点和叶子结点的其余结点，有一个直接前驱，可以有多个直接后继；

因为有直接前驱的结点，其前驱只能有一个（每个孩子只有一个父亲），所以，树不存在交叉的情况

4.  每个结点的数据类型相同，结点中不仅存储数据元素，还存储指向子树的指针/分支

 

树的基本概念和术语

结点的度（degree）——作为根结点的这个结点的分支数/直接后继的数目/孩子数目

树的度——树中结点度的max值

叶子结点——结点度等于0的结点

分支结点——结点度大于0的结点，自然，除了叶子结点的其余结点都是分支结点

结点路径——从树的根到这个结点所经过的分支和结点

结点的层次——根结点所在的层次是1，其余结点的层次数=结点路径中的分支数+1

树的深度——结点层次的最大值。所以只能是某个叶子结点的层次值。

 

二叉树的定义

二叉树是树的一种，在树的基础上它被做出了更严格的结构限定：

1. 每个结点最多有2个叉/分支；普通的树分支数不限

2. 叉分左叉和右叉，等价说法也即孩子分为左孩子和右孩子；普通的树不对孩子的顺序进行记录。

   基于树的结构以及二叉树的特点，可知：二叉树总共有5种基本形态，分别是：

a. 空树

b. 只有一个树根结点

c. 树根结点+树根引申出的左子树，没有右子树

d. 树根结点+树根引申出的右孩子，没有左孩子

e. 树根结点+树根引申出的左孩子+树根引申出的右孩子

头脑小风暴：

3个结点的二叉树有哪几种不同的形态？

可以这样想：

3个结点的二叉树最多3层

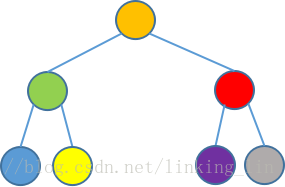
画出一棵3层的满二叉树（每层均有尽可能多的结点的二叉树），然后进行构造

橘 ——绿 + 红（1种）

——绿 + 蓝/黄（2种）

——红 + 紫/灰（2种）

所以，有5种形态的二叉树

可是能把上述人脑思考的过程用算法表达出来么？

在这里我遇到了这个问题，于是我停下来关上电脑，打算在纸上想想如何用程序实现。

那我们就下次见。