1、引例
假如让不了解NBA的社区张大妈猜去年夺冠的球队 【去年总决赛勇士VS骑士,勇士总冠军】 。给出的候选球队依次为w-1-火箭、w-2-勇士、w-3-步行者、w-4-雷霆、e-1-猛龙、e-2-凯尔特人、e-3-76人 和 e-4-骑士这8支队伍。当大妈每猜一次时只能给出正确与错误的反馈时,那么如何让不知情的张大妈能在最少次数下答对?
在不知情的情况下猜测,每个队伍的夺冠概率相同,那么最糟的情况是猜了7次,利用折半法也需要3次。因为当概率均等时,信息熵最大,即不确定性最大。(信息熵概念下文有)那如果大妈平时偶尔了解过NBA并且知道球队分为东西部以及了解某几个球队比较有夺冠实力的话,那不就可以减少猜测的次数了?
这背后就隐藏着决策树了,决策树就是降低信息不确定性的过程。
2、基本概念
引入决策树前,必须要了解“信息熵”以及“信息增益”。
2.1、信息熵
想了解熵的更多信息,可以参阅另外一篇博客。
熵是表示随机变量不确定性的度量。
信息论之父克劳德·香农给出的信息熵的三个性质[1]:
1、单调性,发生概率越高的事件,其携带的信息量越低;
2、非负性,信息熵可以看作为一种广度量,非负性是一种合理的必然;
3、累加性,即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和,这也是广度量的一种体现。
熵(entropy)一般用
H
H
H 表示,单位为比特。当概率均等时,信息熵最大,即不确定性最大。 香农从数学上严格证明了满足上述三个条件的随机变量不确定性度量函数具有唯一形式:
H
(
X
)
=
−
C
∑
x
∈
χ
p
(
x
)
log
p
(
x
)
H(X) = - C\sum_{x\in \chi }p(x)\log p(x)
H(X)=−Cx∈χ∑p(x)logp(x)
其中 C C C 为常数,我们将 C = 1 C=1 C=1 便可以得到信息熵公式。
2.2、条件熵
条件熵(condition entropy)表示在给定已知某种条件
X
X
X 下,事物
Y
Y
Y 的熵即为条件熵
H
(
Y
∣
X
)
H(Y\mid X)
H(Y∣X) ,其公式定义为:
H
(
Y
∣
X
)
=
∑
x
∈
X
p
(
x
)
H
(
Y
∣
x
)
=
−
∑
x
∈
X
p
(
x
)
∑
y
∈
Y
p
(
y
∣
x
)
log
p
(
y
∣
x
)
H(Y\mid X) = \sum_{x\in X}p(x)H(Y\mid x) = - \sum_{x\in X}p(x)\sum_{y\in Y}p(y\mid x)\log p(y\mid x)
H(Y∣X)=x∈X∑p(x)H(Y∣x)=−x∈X∑p(x)y∈Y∑p(y∣x)logp(y∣x)
2.3、信息增益
信息增益(information gain)表示存在某种条件
X
X
X ,它使得条件熵
H
(
Y
∣
X
)
H(Y\mid X)
H(Y∣X) 尽可能的小(也就是“不确定性”减少的多),即当引入信息
X
X
X 之后,事物
Y
Y
Y 的熵变小了。则信息增益记为:
g
(
Y
∣
X
)
=
H
(
Y
)
−
H
(
Y
∣
X
)
g(Y\mid X) = H(Y) - H(Y\mid X)
g(Y∣X)=H(Y)−H(Y∣X)
3、小实例(利用ID3算法处理)
【数据介绍】:14天打篮球情况,包含4种环境特征
【目标】:构造决策树
【数据展示】:
| ID | weather(天气) | temperature(温度) | humidity(湿度) | windy(风况) | play(是否打球) |
|---|---|---|---|---|---|
| 1 | sunny | hot | high | false | no |
| 2 | sunny | hot | high | true | no |
| 3 | overcast | hot | high | false | yes |
| 4 | rainy | mild | high | false | yes |
| 5 | rainy | cool | normal | false | yes |
| 6 | rainy | cool | normal | true | no |
| overcast | cool | normal | true | yes | |
| 8 | sunny | mild | high | false | no |
| 9 | sunny | cool | normal | false | yes |
| 10 | rainy | mild | normal | false | yes |
| 11 | sunny | mild | normal | true | yes |
| 12 | overcast | mild | high | true | yes |
| 13 | overcast | hot | normal | false | yes |
| 14 | rainy | mild | high | true | no |
【开始分析】:
第一步,根据标签值(打没打篮球),计算熵。
14天中有9天打,5天没打,此时熵:
{ χ = { n o , y e s } p ( x = y e s ) = 9 14 p ( x = n o ) = 5 14 \begin{cases}\chi = \left \{ no, yes \right \} \\p(x = yes) = \tfrac{9}{14}\\p(x = no) = \tfrac{5}{14} \end{cases} ⎩⎪⎨⎪⎧χ={no,yes}p(x=yes)=149p(x=no)=145
H ( p l a y ) = − ∑ x ∈ χ p ( x ) log p ( x ) = − 9 14 log 9 14 − 5 14 log 5 14 = 0.940 H(play) = - \sum_{x\in \chi }p(x)\log p(x) = - \frac{9}{14}\log \frac{9}{14} - \frac{5}{14}\log \frac{5}{14} = 0.940 H(play)=−x∈χ∑p(x)logp(x)=−149log149−145log145=0.940
第二步,根据4种特征分别计算条件熵。
-
基于weather条件。
通过数据表格,我们知道:
w e a t h e r ( 14 ) { s u n n y ( 5 ) { y e s ( 2 ) n o ( 3 ) o v e r c a s t ( 4 ) { y e s ( 4 ) n o ( 0 ) r a i n y ( 5 ) { y e s ( 3 ) n o ( 2 ) weather(14) \begin{cases} sunny(5)\begin{cases}yes(2)\\no(3)\end{cases} \\overcast(4)\begin{cases}yes(4)\\no(0)\end{cases} \\rainy(5)\begin{cases}yes(3)\\no(2)\end{cases} \end{cases} weather(14)⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧sunny(5){yes(2)no(3)overcast(4){yes(4)no(0)rainy(5){yes(3)no(2)
那么,计算基于weather的条件熵:
H ( p l a y ∣ w e a t h e r ) = ∑ x ∈ w e a t h e r p ( x ) H ( p l a y ∣ x ) H(play\mid weather) = \sum_{x\in weather}p(x)H(play\mid x) H(play∣weather)=x∈weather∑p(x)H(play∣x)= p ( s u n n y ) H ( p l a y ∣ s u n n y ) + p ( o v e r c a s t ) H ( p l a y ∣ o v e r c a s t ) + p ( r a i n y ) H ( p l a y ∣ r a i n y ) = p(sunny)H(play\mid sunny)+p(overcast)H(play\mid overcast)+p(rainy)H(play\mid rainy) =p(sunny)H(play∣sunny)+p(overcast)H(play∣overcast)+p(rainy)H(play∣rainy)
其中:
{ w e a t h e r = { s u n n y , o v e r c a s t , r a i n y } p l a y = { y e s , n o } p ( s u n n y ) = 5 14 p ( o v e r c a s t ) = 4 14 p ( r a i n y ) = 5 14 ; { p ( y e s ∣ s u n n y ) = 2 5 p ( n o ∣ s u n n y ) = 3 5 p ( y e s ∣ o v e r c a s t ) = 4 4 = 1 p ( n o ∣ o v e r c a s t ) = 0 p ( y e s ∣ r a i n y ) = 3 5 p ( n o ∣ r a i n y ) = 2 5 \begin{cases} weather=\left \{ sunny,overcast,rainy \right \} \\play=\left \{ yes,no \right \} \\p(sunny)=\frac{5}{14} \\p(overcast)=\frac{4}{14} \\p(rainy)=\frac{5}{14} \end{cases} ; \begin{cases} p(yes\mid sunny)=\frac{2}{5} \\p(no\mid sunny)=\frac{3}{5} \\p(yes\mid overcast)=\frac{4}{4}=1 \\p(no\mid overcast)=0 \\p(yes\mid rainy)=\frac{3}{5} \\p(no\mid rainy)=\frac{2}{5} \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧weather={sunny,overcast,rainy}play={yes,no}p(sunny)=145p(overcast)=144p(rainy)=145;⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧p(yes∣sunny)=52p(no∣sunny)=53p(yes∣overcast)=44=1p(no∣overcast)=0p(yes∣rainy)=53p(no∣rainy)=52{ H ( p l a y ∣ s u n y ) = − ∑ y ∈ p l a y p ( y ∣ s u n n y ) log p ( y ∣ s u n n y ) = − 2 5 log 2 5 − 3 5 log 3 5 = 0.971 H ( p l a y ∣ o v e r c a s t ) = − ∑ y ∈ p l a y p ( y ∣ o v e r c a s t ) log p ( y ∣ o v e r c a s t ) = − 1 × log 1 − 0 = 0 H ( p l a y ∣ r a i n y ) = − ∑ y ∈ p l a y p ( y ∣ r a i n y ) log p ( y ∣ r a i n y ) = − 3 5 log 3 5 − 2 5 log 2 5 = 0.971 \begin{cases} H(play\mid suny)=-\sum_{y\in play}p(y\mid sunny)\log p(y\mid sunny)=-\frac{2}{5}\log \frac{2}{5}-\frac{3}{5}\log \frac{3}{5}=0.971 \\H(play\mid overcast)=-\sum_{y\in play}p(y\mid overcast)\log p(y\mid overcast)=-1\times\log 1-0=0 \\H(play\mid rainy)=-\sum_{y\in play}p(y\mid rainy)\log p(y\mid rainy)=-\frac{3}{5}\log \frac{3}{5}-\frac{2}{5}\log \frac{2}{5}=0.971 \end{cases} ⎩⎪⎨⎪⎧H(play∣suny)=−∑y∈playp(y∣sunny)logp(y∣sunny)=−52log52−53log53=0.971H(play∣overcast)=−∑y∈playp(y∣overcast)logp(y∣overcast)=−1×log1−0=0H(play∣rainy)=−∑y∈playp(y∣rainy)logp(y∣rainy)=−53log53−52log52=0.971
所以有:
H ( p l a y ∣ w e a t h e r ) = 5 14 × 0.971 + 4 14 × 0 + 5 14 × 0.971 = 0.693 H(play\mid weather)=\frac{5}{14}\times 0.971+\frac{4}{14}\times 0+\frac{5}{14}\times0.971=0.693 H(play∣weather)=145×0.971+144×0+145×0.971=0.693 -
基于temperautre条件。
通过数据表格,我们知道:
t e m p e r a t u r e ( 14 ) { h o t ( 4 ) { y e s ( 2 ) n o ( 2 ) m i l d ( 6 ) { y e s ( 4 ) n o ( 2 ) c o o l ( 4 ) { y e s ( 3 ) n o ( 1 ) temperature(14) \begin{cases} hot(4)\begin{cases}yes(2)\\no(2)\end{cases} \\mild(6)\begin{cases}yes(4)\\no(2)\end{cases} \\cool(4)\begin{cases}yes(3)\\no(1)\end{cases} \end{cases} temperature(14)⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧hot(4){yes(2)no(2)mild(6){yes(4)no(2)cool(4){yes(3)no(1)
为了不赘述,计算过程同1,可以计算出基于temperature的条件熵:
H ( p l a y ∣ t e m p e r a t u r e ) = ∑ x ∈ t e m p e r a t u r e p ( x ) H ( p l a y ∣ x ) = 4 14 × 1 + 6 14 × 0.918 + 4 14 × 0.811 = 0.911 H(play\mid temperature)=\sum_{x\in temperature}p(x)H(play\mid x)=\frac{4}{14}\times 1+\frac{6}{14}\times 0.918+\frac{4}{14}\times 0.811=0.911 H(play∣temperature)=x∈temperature∑p(x)H(play∣x)=144×1+146×0.918+144×0.811=0.911 -
基于humidity条件。
通过数据表格,我们知道:
h u m i d i t y ( 14 ) { h i g h ( 7 ) { y e s ( 3 ) n o ( 4 ) n o r m a l ( 7 ) { y e s ( 6 ) n o ( 1 ) humidity(14) \begin{cases} high(7)\begin{cases}yes(3)\\no(4)\end{cases} \\normal(7)\begin{cases}yes(6)\\no(1)\end{cases} \end{cases} humidity(14)⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧high(7){yes(3)no(4)normal(7){yes(6)no(1)
计算出基于humidity的条件熵:
H ( p l a y ∣ h u m i d i t y ) = ∑ x ∈ h u m i d i t y p ( x ) H ( p l a y ∣ x ) = 7 14 × 0.985 + 7 14 × 0.592 = 0.788 H(play\mid humidity)=\sum_{x\in humidity}p(x)H(play\mid x)=\frac{7}{14}\times 0.985+\frac{7}{14}\times 0.592=0.788 H(play∣humidity)=x∈humidity∑p(x)H(play∣x)=147×0.985+147×0.592=0.788 -
基于windy条件。
通过数据表格,我们知道:
w i n d y ( 14 ) { f a l s e ( 8 ) { y e s ( 6 ) n o ( 2 ) t r u e ( 6 ) { y e s ( 3 ) n o ( 3 ) windy(14) \begin{cases} false(8)\begin{cases}yes(6)\\no(2)\end{cases} \\true(6)\begin{cases}yes(3)\\no(3)\end{cases} \end{cases} windy(14)⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧false(8){yes(6)no(2)true(6){yes(3)no(3)
计算出基于windy的条件熵:
H ( p l a y ∣ w i n d y ) = ∑ x ∈ w i n d y p ( x ) H ( p l a y ∣ x ) = 8 14 × 0.811 + 6 14 × 1 = 0.892 H(play\mid windy)=\sum_{x\in windy}p(x)H(play\mid x)=\frac{8}{14}\times 0.811+\frac{6}{14}\times 1=0.892 H(play∣windy)=x∈windy∑p(x)H(play∣x)=148×0.811+146×1=0.892
第三步,计算信息增益。
根据第一步计算的熵以及第二步所计算的条件熵,我们可以计算出第一轮的信息增益:
{
g
a
i
n
(
p
l
a
y
∣
w
e
a
t
h
e
r
)
=
H
(
p
l
a
y
)
−
H
(
p
l
a
y
∣
w
e
a
t
h
e
r
)
=
0.940
−
0.693
=
0.247
g
a
i
n
(
p
l
a
y
∣
t
e
m
p
e
r
a
t
u
r
e
)
=
H
(
p
l
a
y
)
−
H
(
p
l
a
y
∣
t
e
m
p
e
r
a
t
u
r
e
)
=
0.940
−
0.911
=
0.029
g
a
i
n
(
p
l
a
y
∣
h
u
m
i
d
i
t
y
)
=
H
(
p
l
a
y
)
−
H
(
p
l
a
y
∣
h
u
m
i
d
i
t
y
)
=
0.940
−
0.788
=
0.152
g
a
i
n
(
p
l
a
y
∣
w
i
n
d
y
)
=
H
(
p
l
a
y
)
−
H
(
p
l
a
y
∣
w
i
n
d
y
)
=
0.940
−
0.892
=
0.048
\begin{cases} gain(play\mid weather)=H(play)-H(play\mid weather)=0.940-0.693=0.247 \\gain(play\mid temperature)=H(play)-H(play\mid temperature)=0.940-0.911=0.029 \\gain(play\mid humidity)=H(play)-H(play\mid humidity)=0.940-0.788=0.152 \\gain(play\mid windy)=H(play)-H(play\mid windy)=0.940-0.892=0.048 \end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧gain(play∣weather)=H(play)−H(play∣weather)=0.940−0.693=0.247gain(play∣temperature)=H(play)−H(play∣temperature)=0.940−0.911=0.029gain(play∣humidity)=H(play)−H(play∣humidity)=0.940−0.788=0.152gain(play∣windy)=H(play)−H(play∣windy)=0.940−0.892=0.048
可以得知
g
a
i
n
(
p
l
a
y
∣
w
e
a
t
h
e
r
)
gain(play\mid weather)
gain(play∣weather) 的信息增益最大 ,
所
以
第
一
轮
产
生
的
决
特
征
为
w
e
a
t
h
e
r
\color{red}{所以第一轮产生的决特征为 weather }
所以第一轮产生的决特征为weather,将其设置为决策树的根节点。
此时,根据特征weather的划分后,数据表为:
| ID | weather(天气) | temperature(温度) | humidity(湿度) | windy(风况) | play(是否打球) |
|---|---|---|---|---|---|
| 1 | s u n n y \color{red}{sunny} sunny | hot | high | false | no |
| 2 | s u n n y \color{red}{sunny} sunny | hot | high | true | no |
| 8 | s u n n y \color{red}{sunny} sunny | mild | high | false | no |
| 9 | s u n n y \color{red}{sunny} sunny | cool | normal | false | yes |
| 11 | s u n n y \color{red}{sunny} sunny | mild | normal | true | yes |
| 3 | o v e r c a s t \color{green}{overcast} overcast | hot | high | false | yes |
| 7 | o v e r c a s t \color{green}{overcast} overcast | cool | normal | true | yes |
| 12 | o v e r c a s t \color{green}{overcast} overcast | mild | high | true | yes |
| 13 | o v e r c a s t \color{green}{overcast} overcast | hot | normal | false | yes |
| 4 | r a i n y \color{blue}{rainy} rainy | mild | high | false | yes |
| 5 | r a i n y \color{blue}{rainy} rainy | cool | normal | false | yes |
| 6 | r a i n y \color{blue}{rainy} rainy | cool | normal | true | no |
| 10 | r a i n y \color{blue}{rainy} rainy | mild | normal | false | yes |
| 14 | r a i n y \color{blue}{rainy} rainy | mild | high | true | no |
根据特征 weather 划分后的表格可以清晰的看到,在 weather 为 o v e r c a s t \color{green}{overcast} overcast 的情况下都去打球了。
此时决策树第一步的画法:
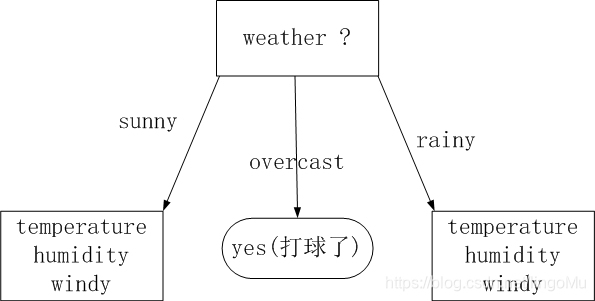
第四步,重复第二、三俩步骤,选出第二个特征。
此时还剩下三个特征,则开始计算除了
o
v
e
r
c
a
s
t
\color{green}{overcast}
overcast 的其余10条数据的熵,因为这10天里,有5天打球5天没打,所以此时的熵为:
H
(
p
l
a
y
)
=
−
5
10
×
log
5
10
−
5
10
×
log
5
10
=
1
H(play)=-\frac{5}{10}\times \log \frac{5}{10}-\frac{5}{10}\times \log \frac{5}{10}=1
H(play)=−105×log105−105×log105=1
和第一轮一样的处理流程,我们分别计算余下的三个特征的条件熵:
-
基于 temperature 的条件熵。
通过划分后的数据表格,我们知道:
t e m p e r a t u r e ( 10 ) { h o t ( 2 ) { y e s ( 0 ) n o ( 2 ) m i l d ( 5 ) { y e s ( 3 ) n o ( 2 ) c o o l ( 3 ) { y e s ( 2 ) n o ( 1 ) temperature(10) \begin{cases} hot(2)\begin{cases}yes(0)\\no(2)\end{cases} \\mild(5)\begin{cases}yes(3)\\no(2)\end{cases} \\cool(3)\begin{cases}yes(2)\\no(1)\end{cases} \end{cases} temperature(10)⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧hot(2){yes(0)no(2)mild(5){yes(3)no(2)cool(3){yes(2)no(1)H ( p l a y ∣ t e m p e r a t u r e ) = ∑ x ∈ t e m p e r a t u r e p ( x ) H ( p l a y ∣ x ) H(play\mid temperature) = \sum_{x\in temperature}p(x)H(play\mid x) H(play∣temperature)=x∈temperature∑p(x)H(play∣x)
= p ( h o t ) H ( p l a y ∣ h o t ) + p ( m i l d ) H ( p l a y ∣ m i l d ) + p ( c o o l ) H ( p l a y ∣ c o o l ) =p(hot)H(play\mid hot)+p(mild)H(play\mid mild)+p(cool)H(play\mid cool) =p(hot)H(play∣hot)+p(mild)H(play∣mild)+p(cool)H(play∣cool)
其中:
{ p ( h o t ) = 2 10 p ( m i l d ) = 5 10 p ( c o o l ) = 3 10 ; { p ( y e s ∣ h o t ) = 0 p ( n o ∣ h o t ) = 1 p ( y e s ∣ m i l d ) = 3 5 p ( n o ∣ m i l d ) = 2 5 p ( y e s ∣ c o o l ) = 2 3 p ( y e s ∣ c o o l ) = 1 3 \begin{cases}p(hot)=\frac{2}{10} \\p(mild)=\frac{5}{10} \\p(cool)=\frac{3}{10} \end{cases} ; \begin{cases}p(yes\mid hot)=0 \\p(no\mid hot)=1 \\p(yes\mid mild)=\frac{3}{5} \\p(no\mid mild)=\frac{2}{5} \\p(yes\mid cool)=\frac{2}{3} \\p(yes\mid cool)=\frac{1}{3} \end{cases} ⎩⎪⎨⎪⎧p(hot)=102p(mild)=105p(cool)=103;⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧p(yes∣hot)=0p(no∣hot)=1p(yes∣mild)=53p(no∣mild)=52p(yes∣cool)=32p(yes∣cool)=31{ H ( p l a y ∣ h o t ) = − ∑ y ∈ p l a y p ( y ∣ h o t ) log p ( y ∣ h o t ) = − 0 − 1 × log 1 = 0 H ( p l a y ∣ m i l d ) = − ∑ y ∈ p l a y p ( y ∣ m i l d ) log p ( y ∣ m i l d ) = − 3 5 × log 3 5 − 2 5 × log 2 5 = 0.971 H ( p l a y ∣ c o o l ) = − ∑ y ∈ p l a y p ( y ∣ c o o l ) log p ( y ∣ c o o l ) = − 2 3 × log 2 3 − 1 3 × log 1 3 = 0.918 \begin{cases}H(play\mid hot)=-\sum_{y\in play}p(y\mid hot)\log p(y\mid hot)=-0-1\times \log 1=0 \\H(play\mid mild)=-\sum_{y\in play}p(y\mid mild)\log p(y\mid mild)=-\frac{3}{5}\times \log \frac{3}{5}-\frac{2}{5}\times \log \frac{2}{5}=0.971 \\H(play\mid cool)=-\sum_{y\in play}p(y\mid cool)\log p(y\mid cool)=-\frac{2}{3}\times \log \frac{2}{3}-\frac{1}{3}\times \log \frac{1}{3}=0.918 \end{cases} ⎩⎪⎨⎪⎧H(play∣hot)=−∑y∈playp(y∣hot)logp(y∣hot)=−0−1×log1=0H(play∣mild)=−∑y∈playp(y∣mild)logp(y∣mild)=−53×log53−52×log52=0.971H(play∣cool)=−∑y∈playp(y∣cool)logp(y∣cool)=−32×log32−31×log31=0.918
所以有:
H ( p l a y ∣ t e m p e r a t u r e ) = ∑ x ∈ t e m p e r a t u r e p ( x ) H ( p l a y ∣ x ) = 2 10 × 0 + 5 10 × 0.971 + 3 10 × 0.918 = 0.761 H(play\mid temperature)=\sum_{x\in temperature}p(x)H(play\mid x)=\frac{2}{10}\times 0+\frac{5}{10}\times 0.971+\frac{3}{10}\times 0.918=0.761 H(play∣temperature)=x∈temperature∑p(x)H(play∣x)=102×0+105×0.971+103×0.918=0.761 -
基于 humidity 的条件熵。
通过划分后的数据表格,我们知道:
h u m i d i t y ( 10 ) { h i g h ( 5 ) { y e s ( 1 ) n o ( 4 ) n o r m a l ( 5 ) { y e s ( 4 ) n o ( 1 ) humidity(10) \begin{cases} high(5)\begin{cases}yes(1)\\no(4)\end{cases} \\normal(5)\begin{cases}yes(4)\\no(1)\end{cases} \end{cases} humidity(10)⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧high(5){yes(1)no(4)normal(5){yes(4)no(1)
同上,计算得:
H ( p l a y ∣ h u m i d i t y ) = ∑ x ∈ h u m i d i t y p ( x ) H ( p l a y ∣ x ) = 5 10 × 0.722 + 5 10 × 0.722 = 0.722 H(play\mid humidity)=\sum_{x\in humidity}p(x)H(play\mid x)=\frac{5}{10}\times0.722+\frac{5}{10}\times0.722=0.722 H(play∣humidity)=x∈humidity∑p(x)H(play∣x)=105×0.722+105×0.722=0.722 -
基于 windy 的条件熵。
通过划分后的数据表格,我们知道:
w i n d y ( 10 ) { f a l s e ( 6 ) { y e s ( 4 ) n o ( 2 ) t r u e ( 4 ) { y e s ( 1 ) n o ( 3 ) windy(10) \begin{cases} false(6)\begin{cases}yes(4)\\no(2)\end{cases} \\true(4)\begin{cases}yes(1)\\no(3)\end{cases} \end{cases} windy(10)⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧false(6){yes(4)no(2)true(4){yes(1)no(3)
同上,计算得:
H ( p l a y ∣ w i n d y ) = ∑ x ∈ w i n d y p ( x ) H ( p l a y ∣ x ) = 6 10 × 0.918 + 4 10 × 0.811 = 0.875 H(play\mid windy)=\sum_{x\in windy}p(x)H(play\mid x)=\frac{6}{10}\times0.918+\frac{4}{10}\times0.811=0.875 H(play∣windy)=x∈windy∑p(x)H(play∣x)=106×0.918+104×0.811=0.875 -
计算新一轮的信息增益,并选出最大的作为下一个决策特征。
第二轮的信息增益为:
{ g a i n ( p l a y ∣ t e m p e r a t u r e ) = H ( p l a y ) − H ( p l a y ∣ t e m p e r a t u r e ) = 1 − 0.761 = 0.0.239 g a i n ( p l a y ∣ h u m i d i t y ) = H ( p l a y ) − H ( p l a y ∣ h u m i d i t y ) = 1 − 0.722 = 0.278 g a i n ( p l a y ∣ w i n d y ) = H ( p l a y ) − H ( p l a y ∣ w i n d y ) = 1 − 0.875 = 0.125 \begin{cases} gain(play\mid temperature)=H(play)-H(play\mid temperature)=1-0.761=0.0.239 \\gain(play\mid humidity)=H(play)-H(play\mid humidity)=1-0.722=0.278 \\gain(play\mid windy)=H(play)-H(play\mid windy)=1-0.875=0.125 \end{cases} ⎩⎪⎨⎪⎧gain(play∣temperature)=H(play)−H(play∣temperature)=1−0.761=0.0.239gain(play∣humidity)=H(play)−H(play∣humidity)=1−0.722=0.278gain(play∣windy)=H(play)−H(play∣windy)=1−0.875=0.125
可知, g a i n ( p a l y ∣ h u m i d i t y ) gain(paly\mid humidity) gain(paly∣humidity) 最大,第二轮产生的决策特征为 h u m i d i t y \color{red}{humidity} humidity 。此时,根据特征 humidity 的划分后,数据表为:
ID weather(天气) temperature(温度) humidity(湿度) windy(风况) play(是否打球) 1 s u n n y \color{red}{sunny} sunny hot h i g h \color{red}{high} high false no 2 s u n n y \color{red}{sunny} sunny hot h i g h \color{red}{high} high true no 8 s u n n y \color{red}{sunny} sunny mild h i g h \color{red}{high} high false no 4 r a i n y \color{blue}{rainy} rainy mild h i g h \color{red}{high} high false yes 14 r a i n y \color{blue}{rainy} rainy mild h i g h \color{red}{high} high true no 9 s u n n y \color{red}{sunny} sunny cool n o r m a l \color{blue}{normal} normal false yes 11 s u n n y \color{red}{sunny} sunny mild n o r m a l \color{blue}{normal} normal false yes 5 r a i n y \color{blue}{rainy} rainy cool n o r m a l \color{blue}{normal} normal false yes 6 r a i n y \color{blue}{rainy} rainy cool n o r m a l \color{blue}{normal} normal true no 10 r a i n y \color{blue}{rainy} rainy mild n o r m a l \color{blue}{normal} normal false yes 3 o v e r c a s t \color{green}{overcast} overcast hot high false yes 7 o v e r c a s t \color{green}{overcast} overcast cool normal true yes 12 o v e r c a s t \color{green}{overcast} overcast mild high true yes 13 o v e r c a s t \color{green}{overcast} overcast hot normal false yes 根据特征 humidity划分后的表格可以清晰的看到,在 weather 为 s u n n y \color{red}{sunny} sunny 并且 humidity 为 h i g h t \color{red}{hight} hight 的情况下都没打球,在 weather 为 s u n n y \color{red}{sunny} sunny 并且 humidity 为 n o r m a l \color{blue}{normal} normal 的情况下都打球了。
所以此时补充决策树的画法:
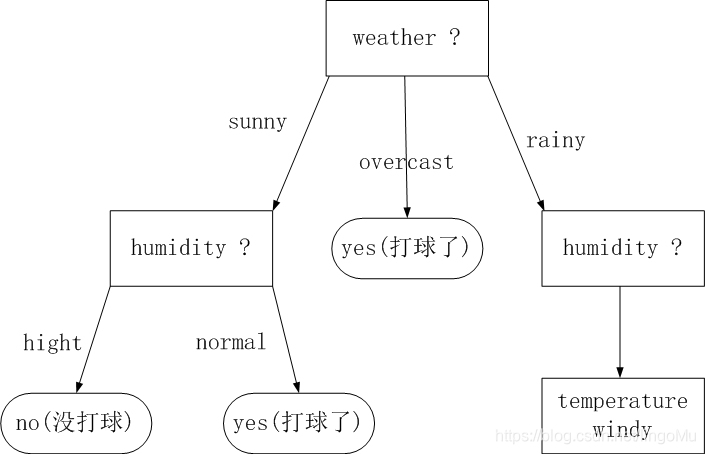
第五步,重复二、三俩步骤,选出第三个特征。
。。。 。。。
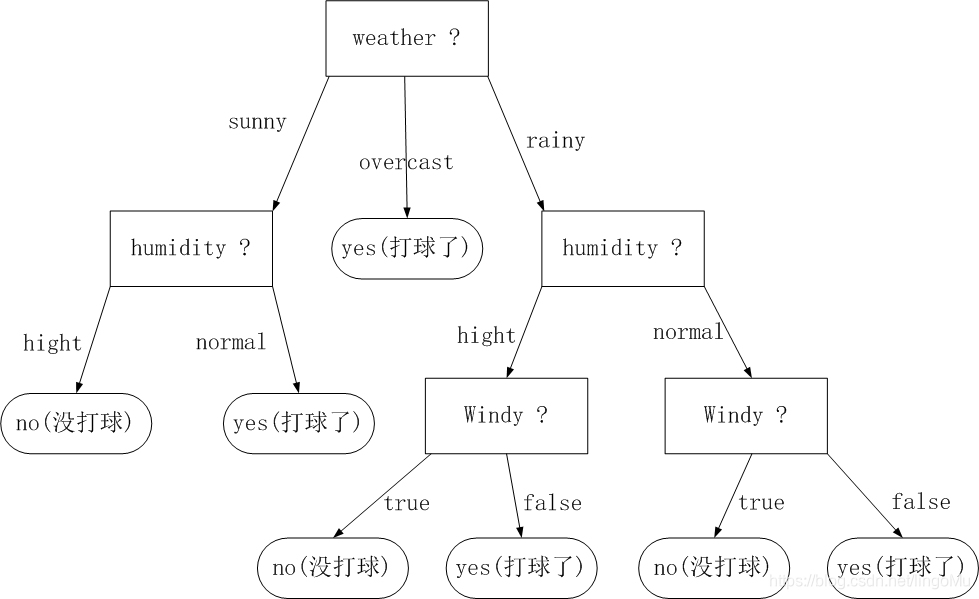
后面运算以及表格的变化都与前面的操作相似,由于篇幅有限,这里就不赘述了,直接给出最后的分划数据表以及决策树。
第三个选出来的特征为 windy ,然后全部决策并划分结束。
| ID | weather(天气) | temperature(温度) | humidity(湿度) | windy(风况) | play(是否打球) |
|---|---|---|---|---|---|
| 4 | r a i n y \color{blue}{rainy} rainy | mild | h i g h \color{red}{high} high | f a l s e \color{red}{false} false | yes |
| 5 | r a i n y \color{blue}{rainy} rainy | cool | n o r m a l \color{blue}{normal} normal | f a l s e \color{red}{false} false | yes |
| 10 | r a i n y \color{blue}{rainy} rainy | mild | n o r m a l \color{blue}{normal} normal | f a l s e \color{red}{false} false | yes |
| 14 | r a i n y \color{blue}{rainy} rainy | mild | h i g h \color{red}{high} high | t r u e \color{blue}{true} true | no |
| 6 | r a i n y \color{blue}{rainy} rainy | cool | n o r m a l \color{blue}{normal} normal | t r u e \color{blue}{true} true | no |
| 1 | s u n n y \color{red}{sunny} sunny | hot | h i g h \color{red}{high} high | false | no |
| 2 | s u n n y \color{red}{sunny} sunny | hot | h i g h \color{red}{high} high | true | no |
| 8 | s u n n y \color{red}{sunny} sunny | mild | h i g h \color{red}{high} high | false | no |
| 9 | s u n n y \color{red}{sunny} sunny | cool | n o r m a l \color{blue}{normal} normal | false | yes |
| 11 | s u n n y \color{red}{sunny} sunny | mild | n o r m a l \color{blue}{normal} normal | false | yes |
| 3 | o v e r c a s t \color{green}{overcast} overcast | hot | high | false | yes |
| 7 | o v e r c a s t \color{green}{overcast} overcast | cool | normal | true | yes |
| 12 | o v e r c a s t \color{green}{overcast} overcast | mild | high | true | yes |
| 13 | o v e r c a s t \color{green}{overcast} overcast | hot | normal | false | yes |
最后的决策树画法:
参考
- python与机器学习实战







 本文详细介绍了决策树中的ID3和C4.5算法,通过一个具体的小实例展示了如何利用ID3算法处理数据,解释了信息熵、条件熵和信息增益等基本概念,逐步构建决策树的过程。
本文详细介绍了决策树中的ID3和C4.5算法,通过一个具体的小实例展示了如何利用ID3算法处理数据,解释了信息熵、条件熵和信息增益等基本概念,逐步构建决策树的过程。
















 4496
4496

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








