逆波兰表达式的程序计算

首先，我们得对三种表达式有一个简单了解：

前缀表达式：操作符在操作数前面，又叫波兰表达式。

中缀表达式：操作符在操作数之间。

后缀表达式：操作符在操作数后面，又叫逆波兰表达式。

为什么会有这三种表达式呢？

本来，有中缀表达式形如“1+((2+3)×4)-5”就够了，很方便人们理解，

但后来计算机不干了，它不理解，准确的说，我们比较难让计算机理解我们的理解。

哈哈哈，有点绕。

于是后来就有了后缀表达式，方便计算机理解。

其次，中缀表达式转化为后缀表达式的逻辑过程是怎样的呢？

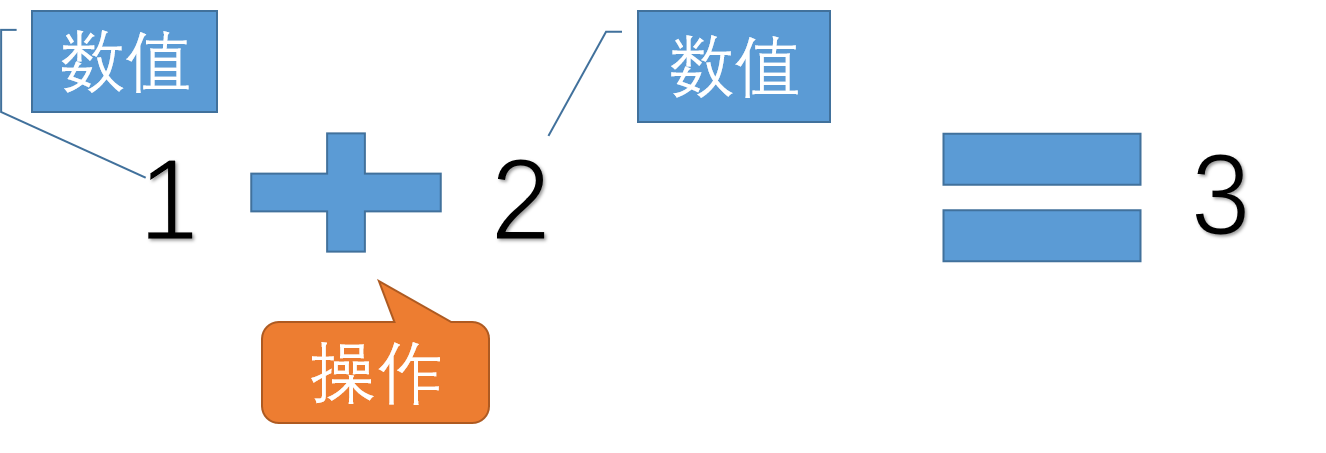
这是一个中缀表达式：

我们可以看到，中缀表达式由三部分组成：两个数值+1个操作符，它的结果是一个数值：

那么，根据我们对中缀表达式的研究，不难得出后缀表达式的表示方法：

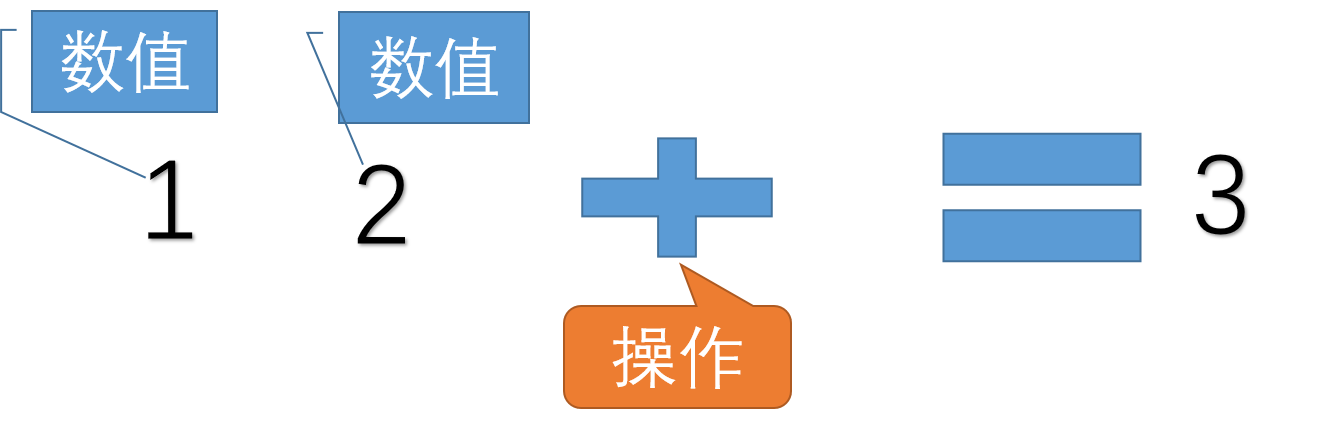 仍然还是：两个数值+1个操作符，结果是一个数值。

更复杂些？

不急，一步步来：

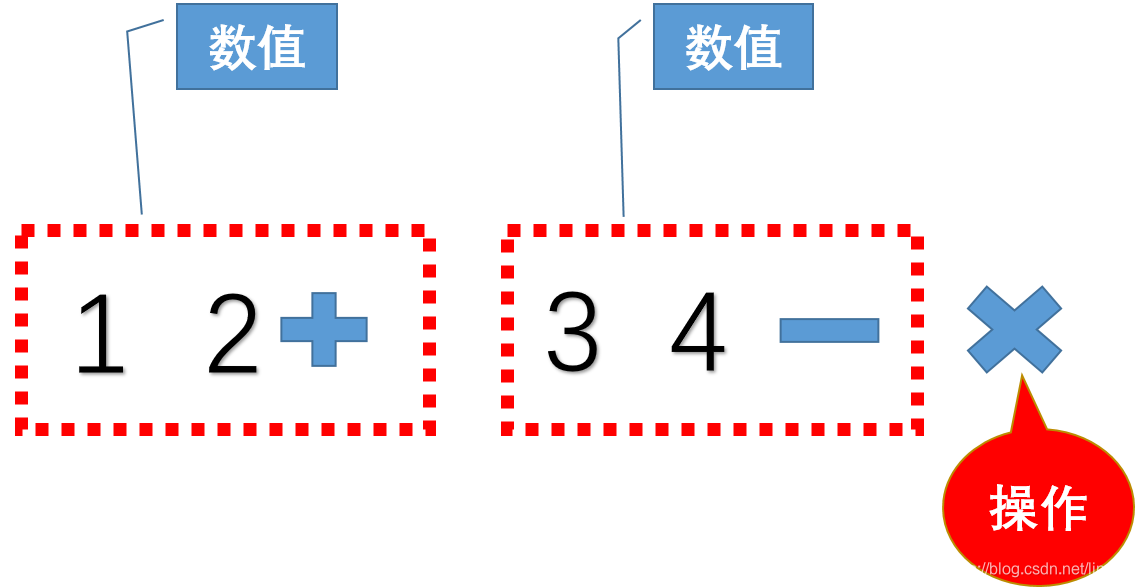
先把1 + 2变成1 2+ ；3 - 4变成3 4 -  ，不要忘记表达式的结果是一个数值，所以：

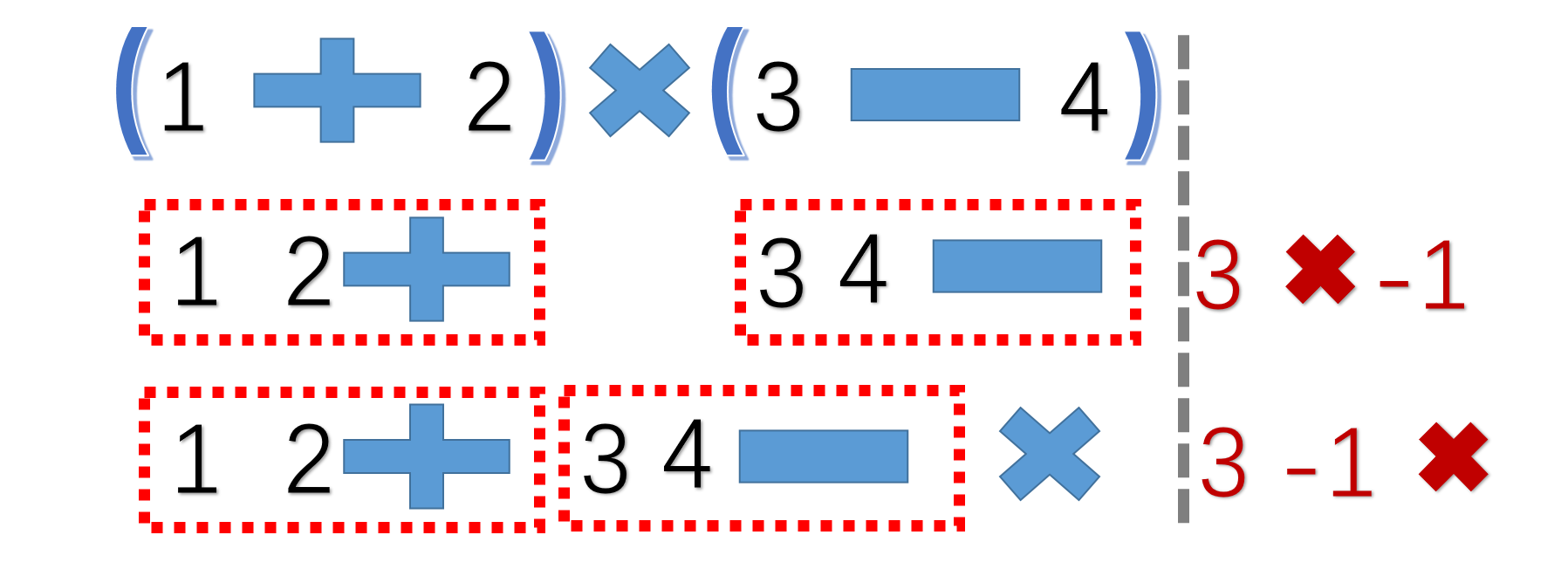
所以我们可以把红色虚框里面看成一个数，即变成了3 ✖ -1， 最基础的模型 

最后的得到结果：1 2+ 3 4 - ✖

接下来，程序的运算逻辑

仔细观察上面的后缀表达式：

 

 

 

 

 

 

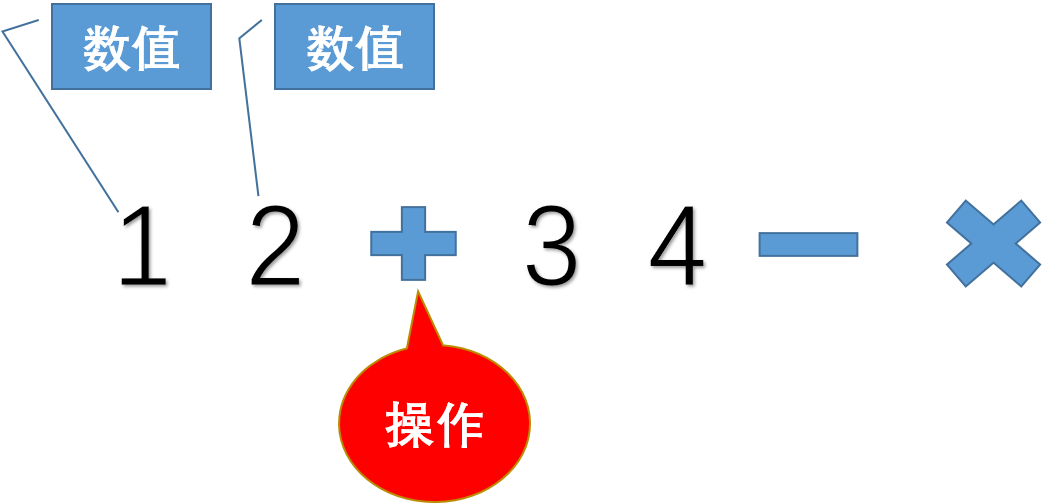
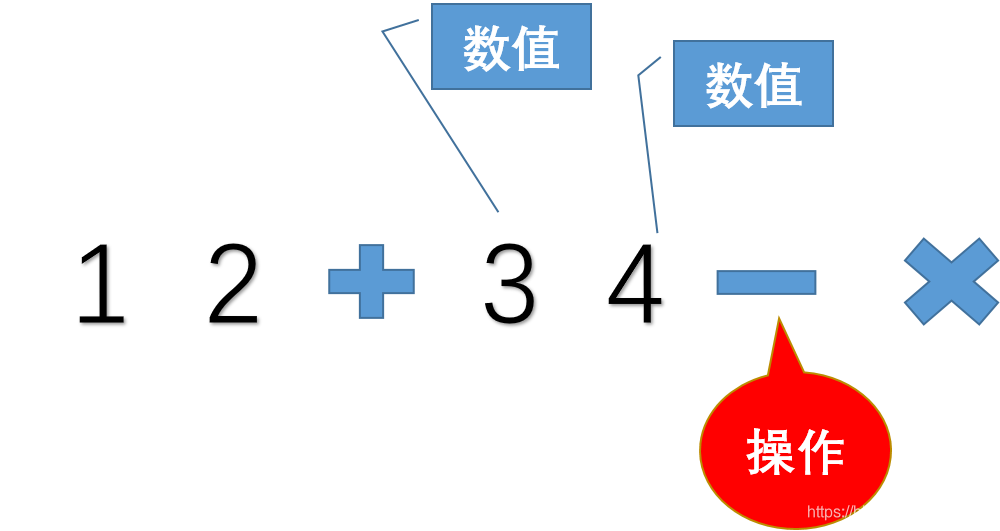
后缀表达式相比于中缀表达式，

最大的优点是运算顺序从左往右走就好了，没有了括号，没有了乘除优先之类的。

其次是“2数值1操作符的特性”，可以很方便的利用动态数组模拟运算过程。

代码的一些注意事项：

①这里不考虑除法（偷懒）。

②resize() 函数改变当前vector的大小为size。

③算法的核心思想是：

从左往右扫描整个表达式，遇到数字就把它放到动态数组中保存起来，

遇到操作符，由于后缀表达式的特性，我们取操作符左边最靠近的两个数值，即动态数组中最后的两个元素，进行操作。

最后，得到一个结果。

代码：

#include<iostream>
#include<vector>
using namespace std;

vector<int> ans;

//字符串转换为数字 
int trans(string s)
{
	int sum=0;
	for(unsigned int i=0; i<s.length(); i++)
	{
		sum=sum*10+s[i]-'0';
	}
	return sum;
}

int main()
{
	ans.clear();//清空数组
	string temp;
	int num=0;
	while(cin>>temp)
	{
		if(temp=="+")
		{
			num=ans[ans.size()-2]+ans[ans.size()-1];
			ans.resize(ans.size()-2);//改变大小
		}
		else if(temp=="-")
		{
			num=ans[ans.size()-2]-ans[ans.size()-1];
			ans.resize(ans.size()-2);
		}
		else if(temp=="*")
		{
			num=ans[ans.size()-2]*ans[ans.size()-1];
			ans.resize(ans.size()-2);
		}
		else//那就是数字了
		{
			num=trans(temp);//把字符串变成数字
		}
		ans.push_back(num);//把数字放到动态数组最后面
	}
	cout<<ans[0]<<endl;

	return 0;
}

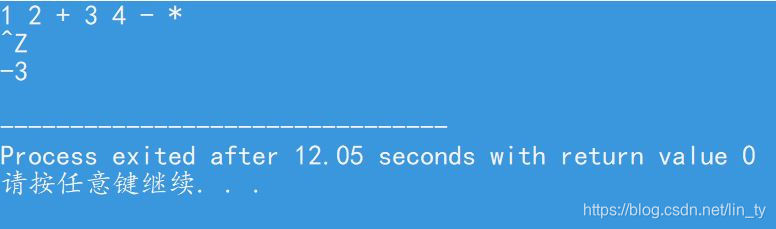
顺带一提，因为这里只是利用到了动态数组的两个操作：

1.往数组尾添加元素

2.取最后面两个元素

和栈很像，所以逆波兰表达式也经常用栈来计算。