ovo以及ovr的直观理解

多分类问题与二分类问题关系

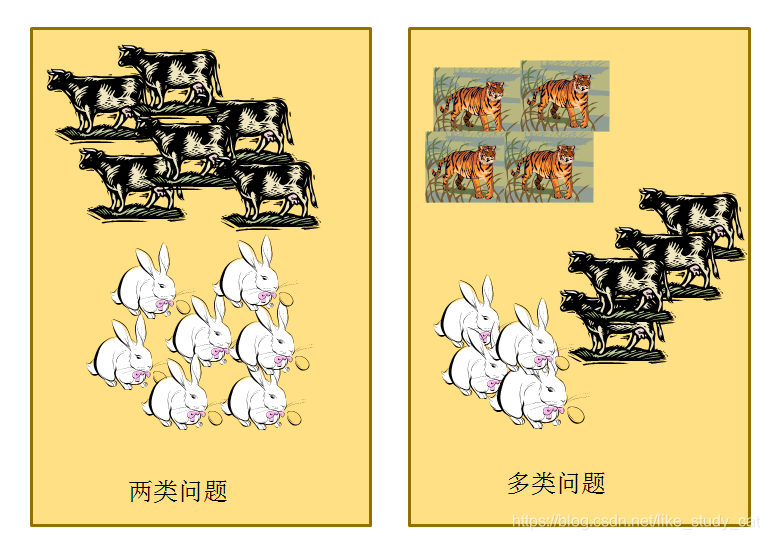首先，两类问题是分类问题中最简单的一种。其次，很多多类问题可以被分解为多个两类问题进行求解（请看下文分解）。所以，历史上有很多算法都是针对两类问题提出的。下面我们来分析如何处理多分类问题：

直接分成多类

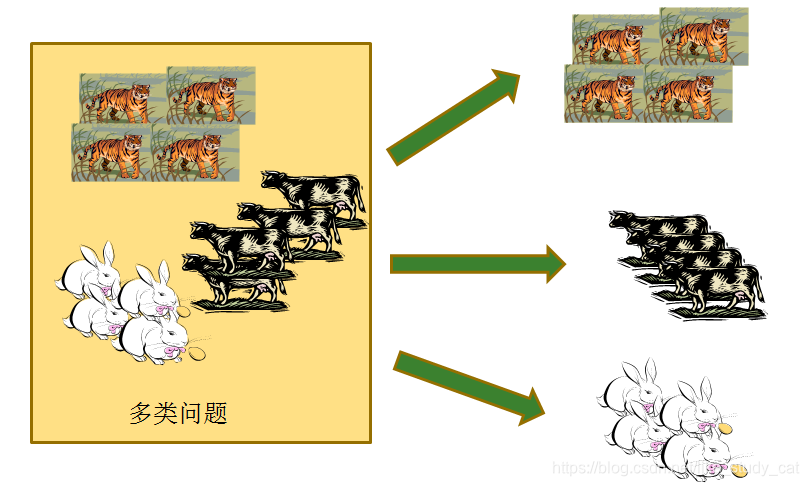
一对一的策略（OVO）

给定数据集D这里有N个类别，这种情况下就是将这些类别两两配对，从而产生N(N−1)2个二分类任务，在测试的时候把样本交给这些分类器，然后进行投票。
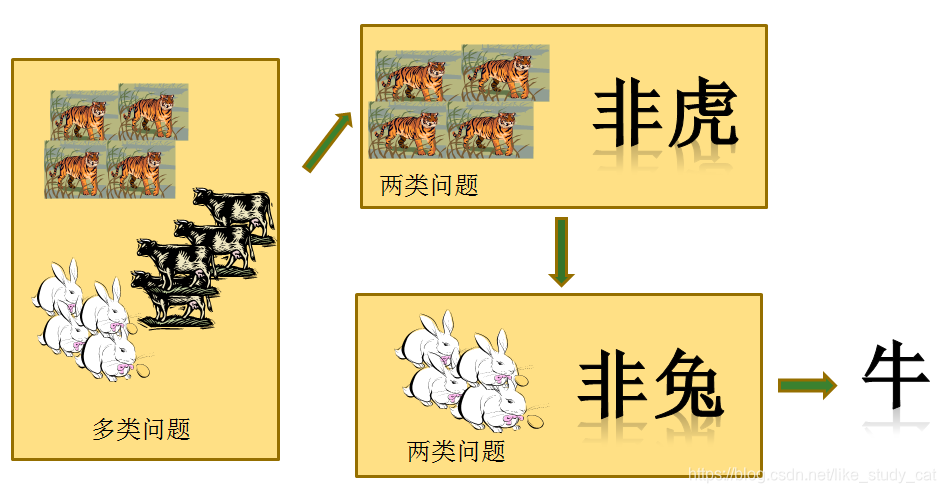
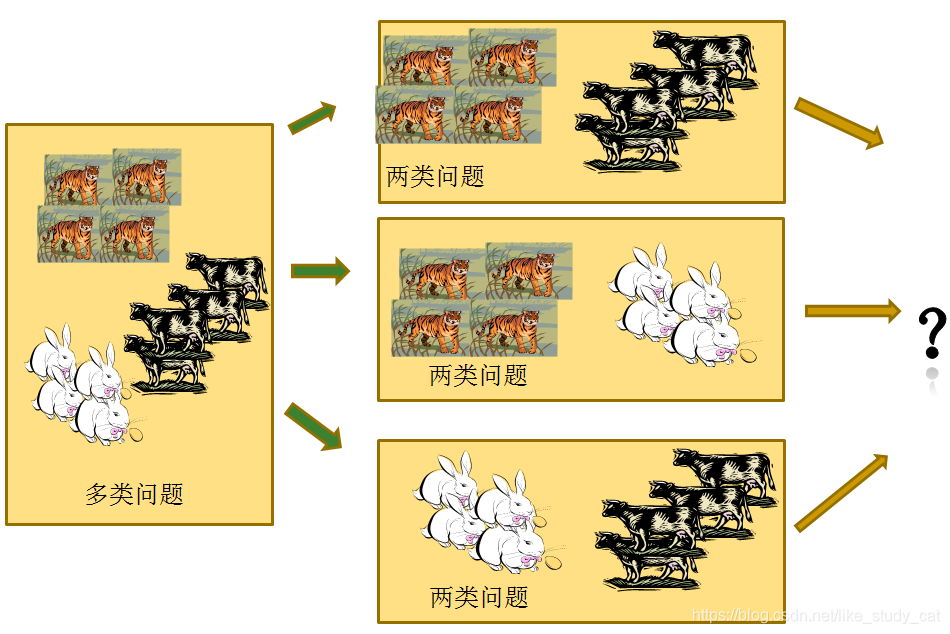一对其余策略（ovr）
将每一次的一个类作为正例，其余作为反例，总共训练N个分类器。测试的时候若仅有一个分类器预测为正的类别则对应的类别标记作为最终分类结果，若有多个分类器预测为正类，则选择置信度最大的类别作为最终分类结果。

多标签问题与二分类问题关系

面临的问题： 图片的标签数目不是固定的，有的有一个标签，有的有两个标签，但标签的种类总数是固定的，比如为5类。

解决该问题： 采用了标签补齐的方法，即缺失的标签全部使用0标记，这意味着，不再使用one-hot编码。例如：标签为：-1,1,1,-1,1 ;-1表示该类标签没有，1表示该类标签存在，则这张图片的标签编码为：

0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1

2.如何衡量损失？

计算出一张图片各个标签的损失，然后取平均值。

3.如何计算精度

计算出一张图片各个标签的精度，然后取平均值。

该处理方法的本质：把一个多标签问题，转化为了在每个标签上的二分类问题。