代數數是滿足整係數代數方程的數。這即是說若 是一個代數數,那麼必然存在整数
是一個代數數,那麼必然存在整数 令
令 是以下方程的根:
是以下方程的根:
在数论中,超越数是指任何一个不是代数数的数字(通常它是复数)。它满足以下条件——只要它不是任何一个整系数代数方程的根,它即是超越数。最著名的超越数是e以及π。
定义
超越数是代数数的相反,也即是说若 是一个超越数,那么对于任何整数
是一个超越数,那么对于任何整数  都符合:
都符合:
例子
超越数的例子包括:
- 刘维尔
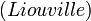 常数:
常数:
它是第一个确认为超越数的数,是于 1844年刘维尔发现的。 - e
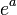 ,其中
,其中 是除0以外的代数数。
是除0以外的代数数。- π(林德曼-魏尔斯特拉斯定理,1882年)
- eπ
 (2的√2次方)。
(2的√2次方)。
更一般地,若 为零和一以外的任何代数数及
为零和一以外的任何代数数及 为无理代数数则
为无理代数数则  必为超越数。这就是格尔丰德-施奈德定理。
必为超越数。这就是格尔丰德-施奈德定理。- sin

- ln
 ,其中
,其中  为非一正有理数。
为非一正有理数。 
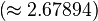 ,
,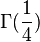
 及
及 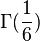
 (参见伽玛函数)。
(参见伽玛函数)。
所有超越数构成的集是一个不可数集。这暗示超越数远多于代数数。可是,现今发现的超越数极少,甚至连 是不是超越数也不知道,因为要证明一个数是超越数或代数数是十分困难的。
是不是超越数也不知道,因为要证明一个数是超越数或代数数是十分困难的。
超越数的发现令一些古代尺规作图问题的不可能性得以证明。这包括著名的化圆为方问题,因  是超越数而被确定为不可能的了。
是超越数而被确定为不可能的了。
参见
代数函数是指包含加、减、乘、除和开方等基本算符的数学函数。非代数函数则被称为超越函数。
例子
y = x2 表示一抛物线的方程,一以x为变量的二次代数函数。
在数学领域中,超越函数与代数函数相反,是指那些不满足任何以多项式方程的函数,即函数不满足以变量自身的多项式为系数的多项式方程。换句话说,超越函数就是"超出"代数函数范围的函数,也就是说函数不能表示为有限次的加、减、乘、除和开方的运算。
严格的说,关于变量 z 的解析函数 ƒ(z) 是超越函数,如果该函数是关于变量z是代数无关的。
对数和指数函数即为超越函数的例子。超越函数这个名词通常被拿来描述三角函数,例如正弦、余弦、正割、余割、余切、正矢、半正矢等。
非超越函数则称为代数函数。代数函数的例子有多项式和平方根函数。
对代数函数进行不定积分运算能够产生超越函数。如对数函数便是在对双曲角围成的面积研究中,对倒数函数y = 1⁄x不定积分得到的。以此方式得到的双曲函数 sinh, cosh, tanh 都是超越函数。
微分代数的某些研究人员研究不定积分如何产生与某类“标准”函数代数无关的函数,例如将三角函数与多项式的合成取不定积分。
量綱分析
在量綱分析里,超越函数是很非常有用的,因为它们只在其引数无量綱时才有意义。因此,超越函数可以是量綱错误的显著来源。例如,log(10 m) 是个毫无意义的表示式。log(10 m)不同于 log(5 m / 3 m) 和 log(3) m,后两者是有实际意义的。log(10 利用对数恒等式,将m)展开为log(10) + log(m)能够更清晰的说明该问题: 一个有量綱的非代数运算会产生毫无意义的结果。
一些例子
以下列出的函数都是超越函数: 除了少数特殊的情况, 对于一般的x不能通过有限次代数运算求出f(x).





 本文介绍了代数数和超越数的概念及其区别。代数数是满足整系数代数方程的数,而超越数则不满足任何整系数代数方程。文中列举了一些著名的超越数例子,并探讨了超越数的重要性及其在解决古代几何问题中的应用。
本文介绍了代数数和超越数的概念及其区别。代数数是满足整系数代数方程的数,而超越数则不满足任何整系数代数方程。文中列举了一些著名的超越数例子,并探讨了超越数的重要性及其在解决古代几何问题中的应用。

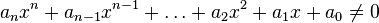




















 1377
1377

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








