第3章 3.5 线性代数相关的函数（MATLAB入门课程）

原创已于 2023-12-31 11:11:49 修改 · 580 阅读

6 ·

CC 4.0 BY-SA版权

文章标签：

#线性代数 #matlab #数学建模

于 2023-11-07 13:05:46 首次发布

MATLAB教程新手入门篇（数学建模清风主讲）专栏收录该内容

61 篇文章

订阅专栏

本文介绍了MATLAB中用于线性代数的六个基本函数，如triu和tril用于处理矩阵的三角部分，eig计算特征值和特征向量，以及norm计算向量和矩阵的范数。通过实例演示了如何生成对称矩阵和调整特征向量顺序。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

讲解视频：可以在bilibili搜索“MATLAB教程新手入门篇——数学建模清风主讲”。

MATLAB教程新手入门篇（数学建模清风主讲，适合零基础同学观看）_哔哩哔哩_bilibili

本小节我们将介绍MATLAB在线性代数中的一些常用函数，以下内容大多仅涉及到初等线性代数的知识，大家可以查阅线性代数的书籍复习相关概念。

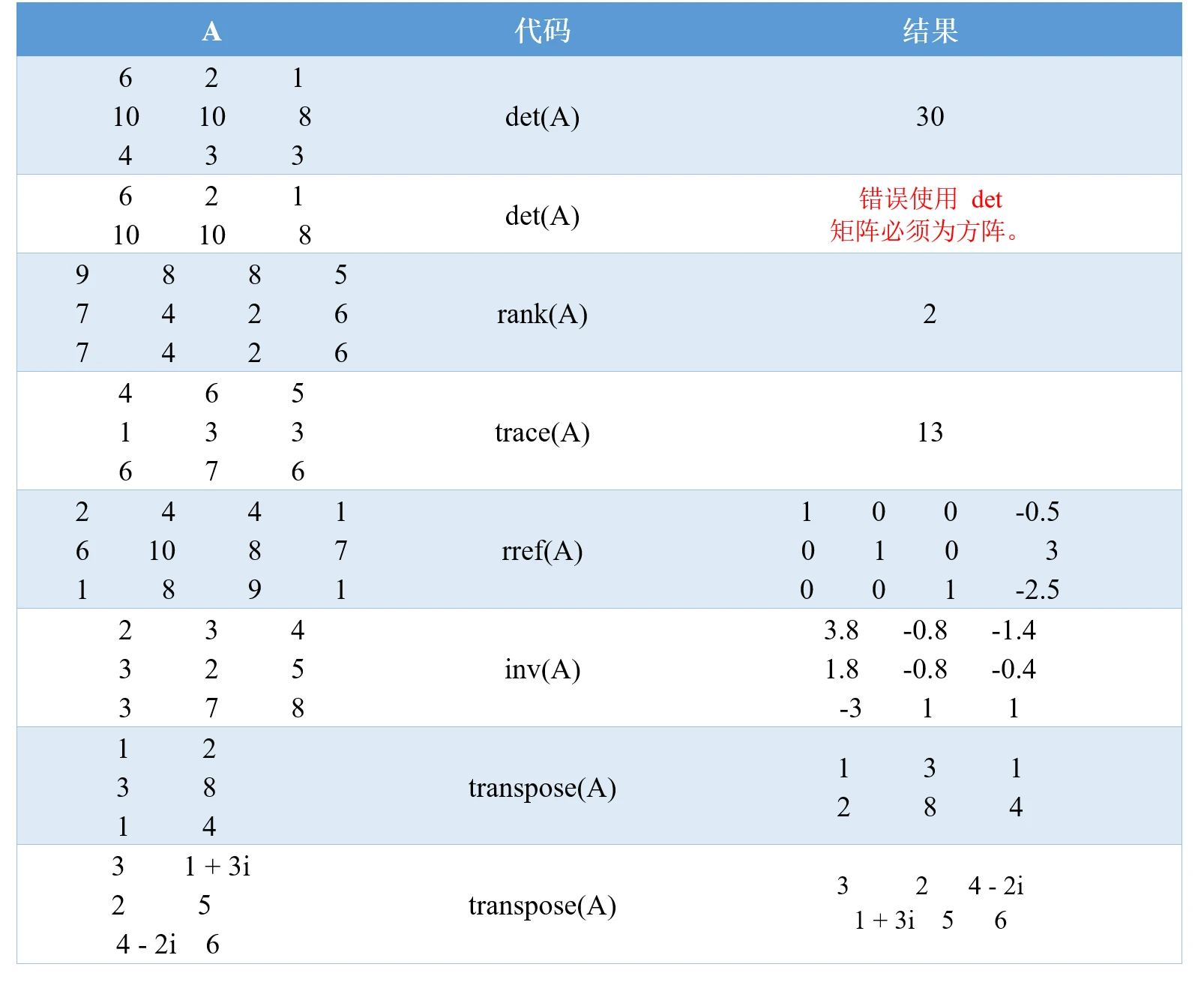
最前面的六个函数

这六个函数都很简单，我们直接来看例子：

triu函数和tril函数

它们用法相同，可分别用来返回矩阵的上三角部分和下三角部分。

triu(A,k)返回A的第k条对角线上以及该对角线上方的元素，其他位置元素用0填充，k等于0时可以简写成triu(A)。
tril(A,k)返回A的第k条对角线上以及该对角线下方的元素，其他位置元素用0填充，k等于0时可以简写成tril(A)。

默认值k = 0是主对角线，k > 0位于主对角线上方，而k < 0位于主对角线下方。

下面我们用这两个函数来做一个有趣的练习题：生成一个n阶（例如n=4）的对称矩阵，里面的每个元素都是位于区间[0, 9]中的随机整数。

答案如下：

n   = 4; 
num   = n*(n-1)/2; 
A   = zeros(n);
A(triu(true(n),1))   = randi([0,9],num,1);
A   = A+A'+diag(randi([0,9],n,1))

% 随机生成的对称矩阵：
     7     6     0     9
     6     3     8     6
     0     8     6     7
     9     6     7     1

这几行代码综合性非常强，核心的思路就是将这个对称矩阵分成三个部分：首先随机生成对称矩阵的上半部分（不包括主对角线），这是一个上三角矩阵；然后将其转置来确保矩阵的元素是对称的；最后使用diag函数生成一个随机的对角矩阵。将上半部分、下半部分以及对角矩阵相加即可得到这个对称矩阵。

具体代码的解释如下：对于一个n阶的对称矩阵，它的上三角部分（不包括主对角线）有n*(n-1)/2个元素，上方代码中将其赋值给num；矩阵A初始化为一个n阶全为0的矩阵；true(n)创建了一个n阶的逻辑矩阵，其中所有元素都为逻辑值1；triu(true(n),1)返回了一个不包括主对角线的上三角的逻辑矩阵，我们用它对A矩阵进行逻辑索引； randi([0,9],num,1)生成了一个有num个元素的向量，其中每个元素都是位于区间[0, 9]中的随机整数；A(triu(true(n),1))选取了矩阵A的上三角部分（不包括主对角线），然后将其赋值为随机生成的整数；A'是矩阵A的转置，由于我们已经填充了A的上三角部分，将它转置我们可以确保下三角部分与上三角部分是对称的；diag(randi([0,9],n,1))生成了一个主对角线上的元素为区间[0, 9]中的随机整数，而其它地方都为0的n阶矩阵；将这三个矩阵相加，即可得到最终的对称矩阵。

以后我们学了循环语句后，还可以利用循环语句生成，虽然循环语句更直观且代码易于编写，但直接基于矩阵操作在MATLAB中通常更高效，尤其是对于大型矩阵。

eig函数

可用来计算方阵的特征值和特征向量，它有两种最基础的用法：

e = eig(A) 返回一个列向量，e中包含方阵A的所有特征值。
[V,D] = eig(A) 返回特征向量构成的矩阵V和特征值构成的对角矩阵D，V中的每一列就是D中对应特征值的特征向量。

我们用MATLAB来验算下：

有同学会有疑惑，为什么MATLAB算出来的特征向量这么奇怪？特征值-1对应的特征向量是[ -0.7071; 0.7071]，特征值3对应的特征向量是[0.7071; 0.7071]。这是因为特征值对应的特征向量不是唯一的，前面可以乘以任意的非零常数。在MATLAB中，eig函数会对特征向量进行缩放，使得各特征值对应的特征向量的模长均为1。

再来看个例子：

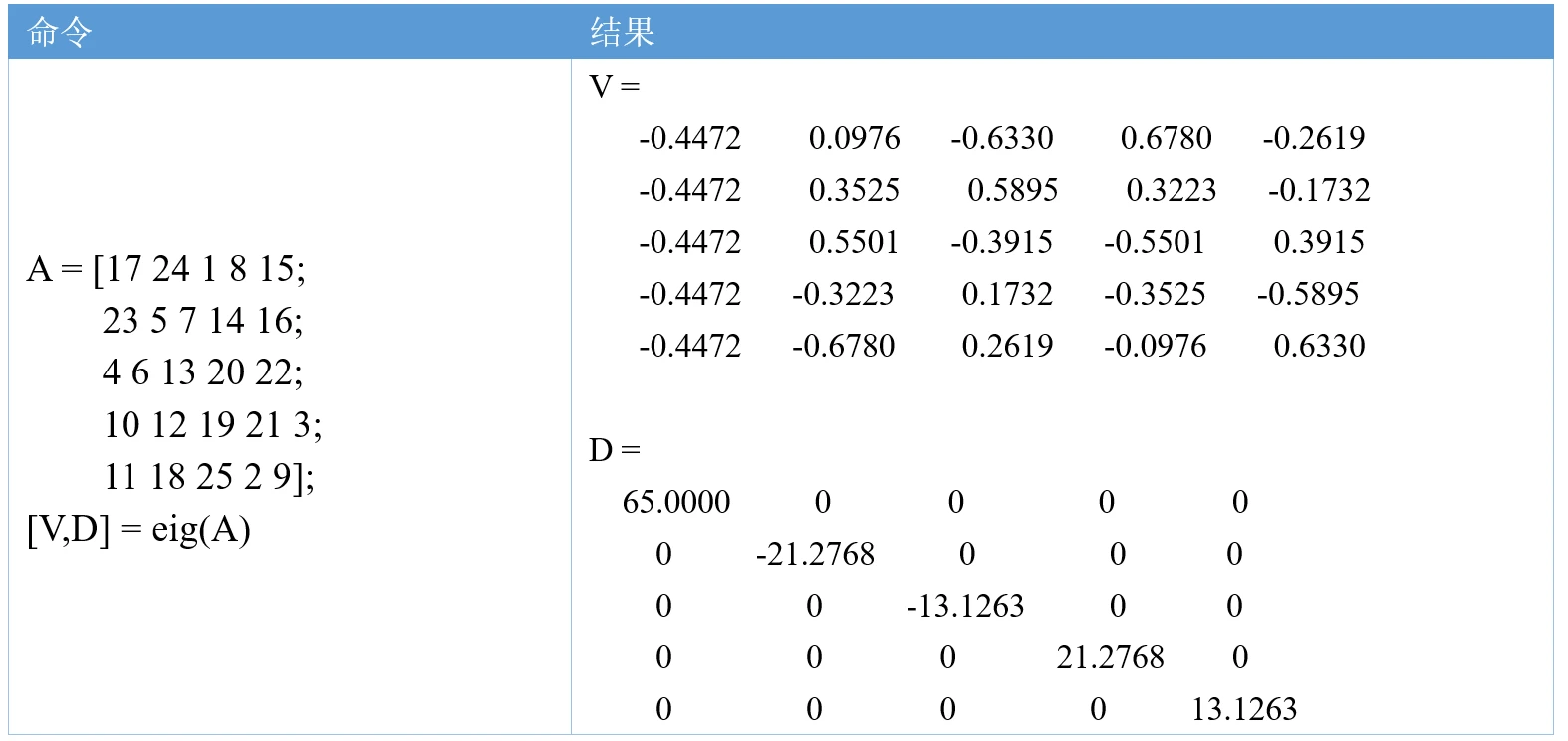
练习题：请你将上方A矩阵的特征值从大到小降序排列，对应的特征向量的顺序也要跟着特征值的顺序改变。

答案如下：

[V, D] = eig(A)
e = diag(D);  % 取出特征值
[sort_e, ind] = sort(e, 'descend');  % 将特征值降序排列
D_new = diag(sort_e)
V_new = V(:, ind)

计算结果如下：

另外，MATLAB计算得到的特征值或特征向量可能会有一定的误差，这是MATLAB的浮点数运算误差导致的，大家以后遇到了有印象即可。

下面我们来介绍最后一个函数：

norm函数

它可以用来计算向量或者矩阵的范数。范数这个概念大家可能没听过，它在机器学习中用的较多。

我们这里只介绍向量的范数，假设向量 $x = \left [x_{1} ,x_{2} ,\dots,x_{n} \right ]$ ，常用的向量范数有下面三种：

1-范数： $\left\| x \right\| _1=\sum_{i=1}^n{\left| x_i \right|}$ , 即对x的元素求绝对值后再求和。

2-范数： $\left\| x \right\| _2=\sqrt{\sum_{i=1}^n{x_{i}^{2}}}$ , 即对x的元素求平方后再求和，然后再开方。

p-范数： $\left\| x \right\| _p=\left( \sum_{i=1}^n{\left| x_i \right|^p} \right) ^{\frac{1}{p}}$ , 即对x元素的绝对值求p次方，再求和，最后再算1/p次幂。

在MATLAB中的调用方法分别为：norm(x,1)、norm(x,2)和norm(x,p)。事实上，1-范数和2-范数都属于p-范数的特例，MATLAB中p默认取2，即norm(x)是norm(x,2)的简写形式，表示计算2-范数。

我们来看几个例子：

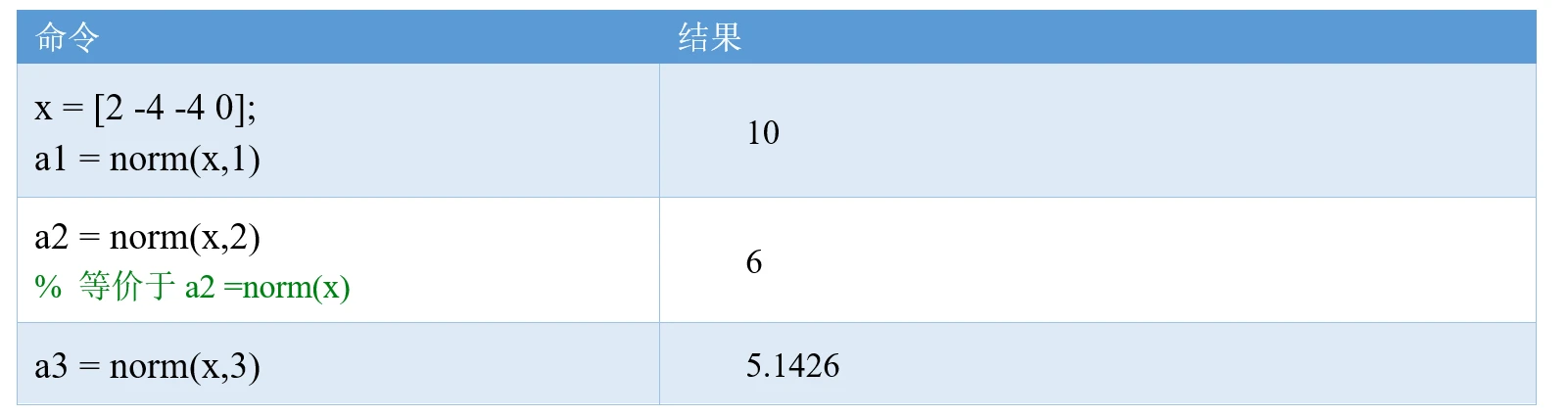
事实上，如果你不会norm函数，也可以用我们之前的方法计算向量的范数：p-范数等价于：sum(abs(x).^p) ^ (1/p)，这里的1/p要加括号。特别地，将p分别取1和2即可得到1-范数和2-范数。

拓展：范数和距离的联系

（1）欧式距离（Euclidean Distance）

欧式距离是最常见的两点之间距离定义的方法，又被称为欧几里得度量，它定义于欧几里得空间中。

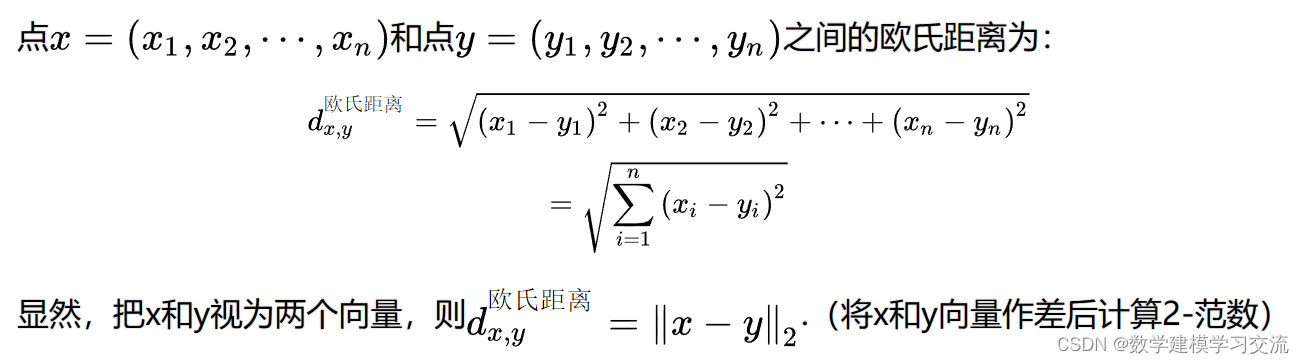
例如x(1, 2)和y(4, 6)直接计算欧氏距离结果5，将它们视为向量：x=[1,2]，y=[4,6]，那么作差后x-y = [-3,-4]，向量[-3,-4]对应的2-范数也为5，和欧氏距离的结果相同。

（2）曼哈顿距离（Manhattan Distance）

假设城市所有的道路是平行且垂直的，如下图所示，你需要驾车从X点到达Y点，那么你的驾驶距离应该如何计算？

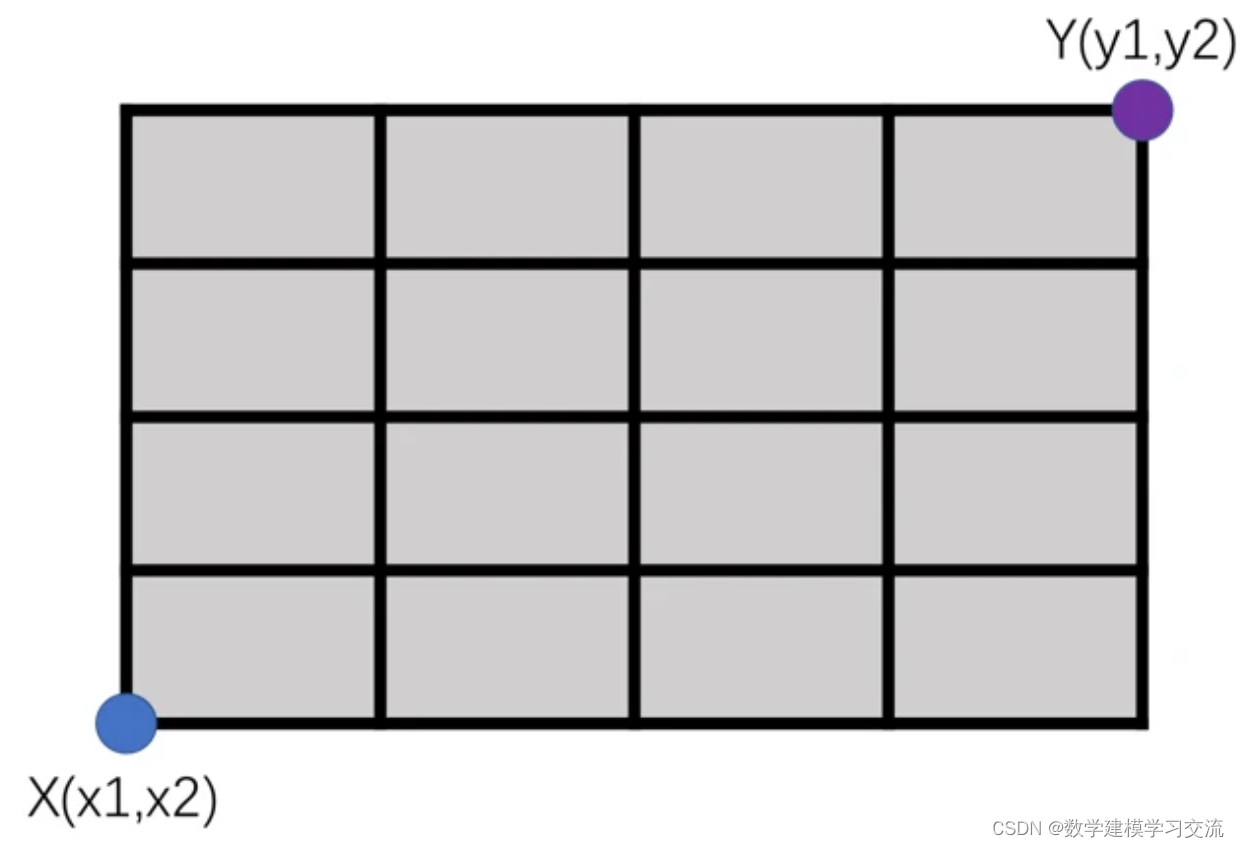
你能直接计算X和Y两点之间的欧式距离作为你的驾驶距离吗？当然不行，除非你乘坐的飞机。这时候，我们可以使用曼哈顿距离来表示实际的驾驶距离。

例如x(1, 2)和y(4, 6)直接计算曼哈顿距离结果7，将它们视为向量作差后得到[-3,-4]，向量[-3,-4]对应的1-范数也为7，和曼哈顿距离的结果相同。

（3）闵可夫斯基距离 (Minkowski Distance)

闵可夫斯基距离（简称为闵氏距离）不是一种特定的距离，而是一组距离的定义。x和y之间的闵氏距离为：

点击下方的优快云专栏阅读下一篇文章：

MATLAB入门课程专栏