根据遍历序列构建二叉树

任务要求：

根据遍历序列构建二叉树，分别实现根据前序和中序序列，中序和后序序列构建二叉树。

相关知识：

掌握三点

①构造二叉树；
②算法思想1；
③算法思想2。

构造二叉树
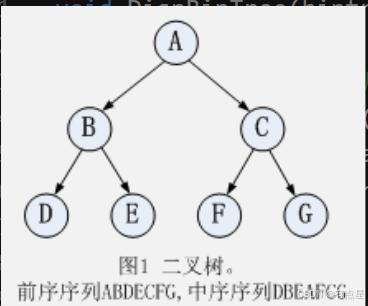
给定一棵二叉树的前序遍历序列和中序遍历序列可以构造出这棵二叉树。例如前序序列是ABDECFG，中序序列是 DBEAFCG，那么这棵二叉树的结构如图 1所示。

算法思想1
给定一棵二叉树的前序遍历序列和中序遍历序列可以构造出这棵二叉树。算法过程如下：
1）根据先序遍历的性质，先序序列中的第一个元素就是根节点root。确定该点在中序序列中的位置k。
2）中序序列中：该位置k的左边都是左子树，右边都是是右子树。
3）左子树的根节点就是根节点root的左孩子，右子树的根节点就是根节点root的右孩子。
 3.1）递归构造左子树
 3.2）递归构造右子树。

算法思想2
给定一棵二叉树的后序遍历序列和中序遍历序列可以构造出这棵二叉树。算法过程如下：
1）根据后序遍历的性质，后序序列中的最后一个元素就是根节点root。确定该点在中序序列中的位置k。
2）中序序列中：该位置k的左边都是左子树，右边都是是右子树。
3）左子树的根节点就是根节点root的左孩子，右子树的根节点就是根节点root的右孩子。
 3.1）递归构造左子树。
 3.2）递归构造右子树。

#include <iostream>
using namespace std;

typedef struct node {
    char data;
    struct node *lchild, *rchild;
} binnode, *bintree;

void CreateBinTreebyPreIn(char *pre, char *in, int n, bintree &T);
void CreateBinTreebyPostIn(char *in, char *post, int n, bintree &T);
void DispBinTree(bintree T);

// 辅助函数，用于通过前序和中序序列查找根节点在中序序列中的位置
int FindRootInInorder(char *in, int inStart, int inEnd, char rootData) {
    for (int i = inStart; i <= inEnd; i++) {
        if (in[i] == rootData) {
            return i;
        }
    }
    return -1; // 不应该发生
}

// 辅助函数，用于通过中序和后序序列查找根节点在中序序列中的位置
int FindRootInPostorder(char *in, int inStart, int inEnd, char rootData) {
    for (int i = inStart; i <= inEnd; i++) {
        if (in[i] == rootData) {
            return i;
        }
    }
    return -1; // 不应该发生
}

void CreateBinTreebyPreIn(char *pre, char *in, int n, bintree &T) {
    if (n <= 0) {
        T = NULL;
        return;
    }
    
    // 创建根节点
    T = new binnode;
    T->data = *pre;
    T->lchild = T->rchild = NULL;
    
    // 在中序序列中找到根节点的位置
    int rootIndex = FindRootInInorder(in, 0, n - 1, *pre);
    
    // 递归构造左子树和右子树
    CreateBinTreebyPreIn(pre + 1, in, rootIndex, T->lchild);
    CreateBinTreebyPreIn(pre + rootIndex + 1, in + rootIndex + 1, n - rootIndex - 1, T->rchild);
}

void CreateBinTreebyPostIn(char *in, char *post, int n, bintree &T) {
    if (n <= 0) {
        T = NULL;
        return;
    }
    
    // 创建根节点
    T = new binnode;
    T->data = post[n - 1];
    T->lchild = T->rchild = NULL;
    
    // 在中序序列中找到根节点的位置
    int rootIndex = FindRootInPostorder(in, 0, n - 1, post[n - 1]);
    
    // 递归构造左子树和右子树
    CreateBinTreebyPostIn(in, post, rootIndex, T->lchild);
    CreateBinTreebyPostIn(in + rootIndex + 1, post + rootIndex, n - rootIndex - 1, T->rchild);
}




int main()
{
    bintree T;
    char *pre,*in,*post;
    int n;
    cin>>n;
    pre=new char[n];
    in=new char[n];
    post=new char[n];
    cin>>pre;
    cin>>in;
    cin>>post;
    CreateBinTreebyPreIn(pre,in,n,T);
    cout<<"\nthe result is:";
    if (T==NULL)
        cout<<"\nnull";
    else
        DispBinTree(T);
    CreateBinTreebyPostIn(in,post,n,T);
    cout<<"\nthe result is:";
    if (T==NULL)
        cout<<"\nnull";
    else
        DispBinTree(T);
    return 0;
}
void DispBinTree(bintree T)
{
    if (T==NULL) return ;
    cout<<T->data;
    if (T->lchild || T->rchild)
    {
        cout<<"(";
        DispBinTree(T->lchild);
        if (T->rchild) cout<<",";
        DispBinTree(T->rchild);
        cout<<")";
    }
}