ERQ：32位转5位仅掉些许精度，来看看两段式后训练量化 | ICML 2024

后训练量化（PTQ）在视觉Transformer（ViTs）领域引起了广泛关注，因为它在模型压缩方面表现出了高效率。然而，现有的方法通常忽视了量化权重和激活之间复杂的相互依赖关系，导致了相当大的量化误差。论文提出了一种名为ERQ的两步PTQ方法，精心设计用于顺序降低激活和权重量化带来的量化误差。ERQ首先引入了激活量化误差减小（Aqer），将激活量化误差的最小化策略性地表述为一个岭回归问题，并通过使用全精度更新权重来解决。随后，ERQ引入了权重量化误差减小（Wqer），采用迭代的方法来减轻由权重量化引起的量化误差。在每次迭代中，采用经验推导出的有效代理来细化量化权重的舍入方向，并结合岭回归求解器以减少权重量化误差。实验结果证明了该方法的有效性。值得注意的是，ERQ在W3A4 ViT-S的准确性上超越了最先进的GPTQ，提升幅度达22.36%。

来源：晓飞的算法工程笔记 公众号，转载请注明出处

论文: ERQ: Error Reduction for Post-Training Quantization of Vision Transformers

• 论文地址：https://arxiv.org/abs/2407.06794

Introduction

---

视觉Transformer（ViTs）显著挑战了卷积神经网络（CNNs），成为计算机视觉领域的新范式。ViTs利用多头自注意力（MHSA）机制来捕捉图像块之间的长距离关系，在各种视觉任务中展现出令人印象深刻的进展。

然而，强大的能力伴随着相当的复杂性。ViTs固有的架构复杂性导致了高计算需求和可观的内存要求，这在资源受限的环境中部署时带来了挑战。为了缓解这一困境，模型量化吸引了业界和学术界的持续关注。量化通过实现权重和激活的低位表示来减少模型复杂性，为高效部署提供了一条有前景的途径。最近，研究人员逐渐关注于视觉Transformer的后训练量化（PTQ），该方法旨在利用一个小型校准数据集和较低的成本对模型进行量化。

为了适应ViTs独特的结构，已经许多研究探索了各种后训练量化（PTQ）方法。例如，为了处理长尾post-Softmax激活，有研究提出了 $log2/log\sqrt{2}$ 量化器和twin uniform量化器。为了管理高度变化的激活，有研究采用了重参数化技术和power-of-two因子。此外，有研究采用进化搜索方法来确定不稳定的缩放因子。然而，现有的方法通常忽视了权重和激活量化之间复杂的相互依赖关系，这在权重-激活量化时导致了相当大的量化误差。

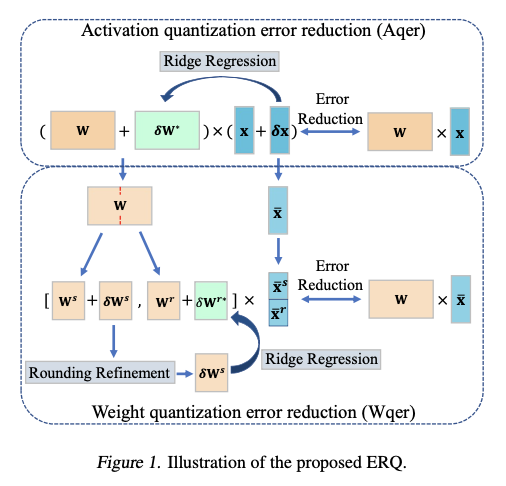
论文提出一种为ViTs量身定制的两步后训练量化方法ERQ，旨在顺序减小由量化激活和权重引起的量化误差。如图1所示，ERQ由两个步骤组成，即激活量化误差减少（Aqer）和权重量化误差减少（Wqer）。Aqer将激活量化引起的量化误差公式化为一个岭回归问题，该问题可以通过权重更新以闭式解的方式解决。随后，引入Wqer以迭代的量化和修正方式减小由权重量化引起的量化误差。特别地，在每次迭代中，量化全精度权重的前半部分，并通过先执行四舍五入细化，后再次解决岭回归问题来减小产生的量化误差。前者推导出输出误差的有效代理，用于细化量化权重的四舍五入方向，以降低量化误差。后者则通过更新剩余的全精度权重进一步减小量化误差。这样的过程持续进行，直到所有权重被准确量化。

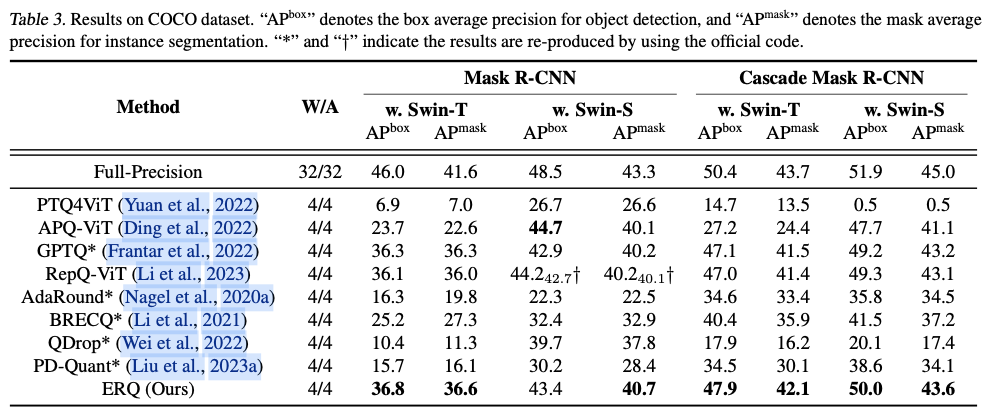
ERQ在对各种ViTs变体（ViT、DeiT和Swin）及任务（图像分类、目标检测和实例分割）进行的广泛实验中证明了其有效性。值得注意的是，在图像分类任务中，ERQ在W3A4 ViT-S上比GPTQ的性能提高了22.36%。

Method

---

相互纠缠的 $\delta \mathbf{x}$ 和 $\delta \mathbf{W}$ 使得找到公式 4 的最优解变得具有挑战性。为使问题变得可处理，将公式 4放宽为两个顺序的子问题，通过分别最小化来自量化激活和权重的误差。如图1所示，首先进行激活量化误差减少 (Aqer)，然后进行权重量化误差减少 (Wqer)。

Activation Quantization Error Reduction

为减轻由激活量化引起的误差，引入激活量化误差减少 (Aqer)，将误差减轻问题形式化为岭回归问题。具体来说，将权重保留为全精度，仅考虑由激活量化误差 $\delta \mathbf{x}$ 引起的均方误差 (MSE)：

KaTeX parse error: Undefined control sequence: \label at position 144: …|_2^2 \right]. \̲l̲a̲b̲e̲l̲{eq:obj-act} \e…

为了最小化公式 5，将其形式化为岭回归问题，其中通过将权重 $\mathbf{W}$ 与调整项 $\delta {\mathbf{W}}^{\ast }$ 相加来完成最小化：

KaTeX parse error: Undefined control sequence: \label at position 519: …f{W}^* \|_2^2. \̲l̲a̲b̲e̲l̲{eq:obj-act1} \…

这里， $\delta {\mathbf{W}}^{\ast }$ 表示通过岭回归计算出的调整项， $\bar{\mathbf{x}}=\mathbf{x}+\delta \mathbf{x}$ 是量化输入， ${\lambda }_1\Vert \delta {\mathbf{W}}^{\ast }{\Vert }_2^2$ 作为正则化项， ${\lambda }_1$ 是控制正则化强度的超参数。公式6构成了岭回归问题。为了最小化它，首先计算其相对于 $\delta {\mathbf{W}}^{\ast }$ 的梯度：

KaTeX parse error: Undefined control sequence: \label at position 384: …a\mathbf{W}^*. \̲l̲a̲b̲e̲l̲{eq:obj-act2} \…

然后，通过将公式 7设置为零来求解 $\delta {\mathbf{W}}^{\ast }$ ：

$$\begin{array}{c}\begin{array}{rl}& \mathbb{E}\left[2(\delta {\mathbf{W}}^{\ast }\bar{\mathbf{x}}+\mathbf{W}\delta \mathbf{x}){\bar{\mathbf{x}}}^T\right]+2{\lambda }_1\delta {\mathbf{W}}^{\ast }=0\\ & \Rightarrow \delta {\mathbf{W}}^{\ast }=-\mathbf{W}\mathbb{E}\left[\delta \mathbf{x}{\bar{\mathbf{x}}}^T\right](\mathbb{E}\left[\bar{\mathbf{x}}{\bar{\mathbf{x}}}^T\right]+{\lambda }_1\mathbf{I}{)}^{-1}.\end{array}\end{array}$$

正则化项 ${\lambda }_1\mathbf{I}$ 确保 $\mathbb{E}\left[\bar{\mathbf{x}}{\bar{\mathbf{x}}}^T\right]+{\lambda }_1\mathbf{I}$ 的逆始终存在，这对计算稳定性至关重要。此外，它抑制了异常值，从而减轻了过拟合，提高了模型的泛化能力。抑制异常值对于随后的权重量化也至关重要，因为它限制了权重的范围。这种限制防止量化点分布在未覆盖的区域，从而增强了量化的表达能力。

在实践中，给定校准数据集，使用 $\frac{1}{N}{\sum }_n^N\delta {\mathbf{x}}_n{\bar{\mathbf{x}}}_n^T$ 和 $\frac{1}{N}{\sum }_n^N{\bar{\mathbf{x}}}_n{\bar{\mathbf{x}}}_n^T$ 分别估计 $\mathbb{E}\left[\delta \mathbf{x}{\bar{\mathbf{x}}}^T\right]$ 和 $\mathbb{E}\left[\bar{\mathbf{x}}{\bar{\mathbf{x}}}^T\right]$ 。这里， $N=B\times T>>D_{in}^s$ ，其中 $B$ 是校准数据集的大小， $T$ 是一张图像的标记数量。请注意， $\delta \mathbf{x}$ 和 $\bar{\mathbf{x}}$ 是在给定输入和量化参数的情况下确定的。在得到 $\delta {\mathbf{W}}^{\ast }$ 后，通过 $\mathbf{W}=\mathbf{W}+\delta {\mathbf{W}}^{\ast }$ 将其合并到网络的权重中。通过这样做，所提出的Aqer明确减轻了从量化激活到权重的量化误差。

Weight Quantization Error Reduction

在进行Aqer后需执行权重量化，提出权重量化误差减少（Wqer）来减轻由此产生的量化误差。在这里，目标被定义为：

KaTeX parse error: Undefined control sequence: \label at position 371: …|_2^2 \right]. \̲l̲a̲b̲e̲l̲{eq:obj-weight0…

注意，在进行Aqer后，激活值被量化。公式9表明输出通道之间的最小化是独立进行的。因此，分别分析每个 ${\mathcal{L}}_i^{\text{MSE}}$ 的最小化。同时对整个全精度权重进行量化会导致无法恢复的量化误差。因此，采用迭代的量化和修正方法，逐步减少由权重量化引起的量化误差。

在每次迭代中，首先对未量化权重的前半部分进行量化，然后减轻由此产生的量化误差。具体来说，从当前的全精度权重 ${\mathbf{W}}_{i,:}$ 和相应的 $\bar{\mathbf{x}}$ 开始。然后，将 $\mathbf{W}$ 划分为两个部分：前半部分 ${\mathbf{W}}_{i,:}^s\in {\mathbb{R}}^{1\times D_{in}^s}$ 用于量化，而剩余部分 ${\mathbf{W}}_{i,:}^r\in {\mathbb{R}}^{1\times D_{in}^r}$ 保持全精度。对应地，从 $\bar{\mathbf{x}}$ 中派生出 ${\bar{\mathbf{x}}}^s\in {\mathbb{R}}^{D_{in}^s}$ 和 ${\bar{\mathbf{x}}}^r\in {\mathbb{R}}^{D_{in}^r}$ ，其中 ${\bar{\mathbf{x}}}^s$ 和 ${\bar{\mathbf{x}}}^r$ 分别包含与 ${\mathbf{W}}_{i,:}^s$ 和 ${\mathbf{W}}_{i,:}^r$ 对应的 $\bar{\mathbf{x}}$ 的行。量化后的 ${\mathbf{W}}_{i,:}^s$ 的量化误差记为 $\delta {\mathbf{W}}_{i,:}^s={\bar{\mathbf{W}}}_{i,:}^s-{\mathbf{W}}_{i,:}^s$ ，由此产生的均方误差（MSE）为：

KaTeX parse error: Undefined control sequence: \label at position 415: …]. \end{split} \̲l̲a̲b̲e̲l̲{eq:obj-weight-…

在这里， ${\mathbf{W}}_{i,:}=[{\mathbf{W}}_{i,:}^s,{\mathbf{W}}_{i,:}^r]$ ， $\bar{\mathbf{x}}=[{\bar{\mathbf{x}}}^s,{\bar{\mathbf{x}}}^r]$ 。为了减轻公式10，首先引入四舍五入优化（Rounding Refinement），在该过程中会细化量化权重的四舍五入方向。比如调整 $\delta {\mathbf{W}}_{i,:}^s$ ，以减少 $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ 本身。然后，在四舍五入优化之后，给定 $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ ，构建一个岭回归（Ridge Regression）问题，通过调整 ${\mathbf{W}}_{i,:}^r$ 来进一步减轻该误差。

Rounding Refinement

最初，目标是调整量化权重的四舍五入方向，以最小化 $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ 。具体来说，对于 ${\mathbf{W}}_{i,:}^s$ 中的第 $j$ 个值，记作 ${\mathbf{W}}_{i,j}^s$ ，量化过程涉及向下取整或向上取整。因此， ${\mathbf{W}}_{i,:}^s$ 的量化误差，记作 $\delta {\mathbf{W}}_{i,j}^s$ ，可以表示为 $\delta {\mathbf{W}}^{s\downarrow }i,j$ 或 $\delta {\mathbf{W}}^{s\uparrow }i,j$ 。这里， $\delta {\mathbf{W}}_{i,j}^{s\downarrow }={\mathbf{W}}_{i,j}^s-{\text{Q}}_{un\downarrow }({\mathbf{W}}_{i,j}^s,b)>0$ 表示采用向下取整策略所产生的误差， $\delta {\mathbf{W}}_{i,j}^{s\uparrow }={\mathbf{W}}_{i,j}^s-{\text{Q}}_{un\uparrow }({\mathbf{W}}_{i,j}^s,b)<0$ 表示采用向上取整策略所产生的误差，其中 $\downarrow /\uparrow$ 表示在公式1中将 $\lfloor \cdot \rceil$ 替换为 $\lfloor \cdot \rfloor$ / $\lceil \cdot \rceil$ 。

选择 $\delta {\mathbf{W}}_{i,:}^s$ 是一个NP难题，其解可以通过混合整数二次规划（MIPQ）进行搜索。然而， $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ 的高计算复杂度使得在合理时间内找到解决方案成为一项挑战。如表1所示，使用 $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ 作为MIPQ的目标消耗了约130小时的巨大时间成本。

• Efficient Proxy

因此，目标是找到 $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ 的一个高效代理。首先，将 $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ 重写为：

KaTeX parse error: Undefined control sequence: \label at position 284: …}}^s \right]. \̲l̲a̲b̲e̲l̲{eq:obj-weight1…

这里， $\Delta$ 表示利用 $\mathbb{E}\left[Z^2\right]=(\mathbb{E}\left[Z\right]{)}^2+\text{Var}\left[Z\right]$ 。

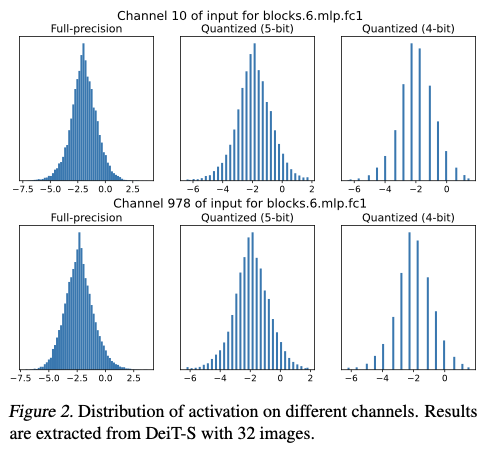
根据中心极限定理，神经网络中的大量乘法和加法运算使得激活值通常呈现出高斯分布，这也是许多以前量化领域研究的基本假设。同时，图2展示了全精度和量化激活的通道分布。可以看出，量化激活仍然表现出近似的高斯分布。

因此，论文认为 ${\bar{\mathbf{x}}}^s$ 的通道分布仍然可以通过高斯分布进行捕捉，并用 $D_{in}^s$ 维的高斯分布 $\mathcal{N}({\mathbf{\mu }}^s,{\mathbf{\Sigma }}^s)$ 对 ${\bar{\mathbf{x}}}^s$ 进行建模，其中 $D_{in}^s$ 是 ${\bar{\mathbf{x}}}^s$ 的维度， ${\mathbf{\mu }}^s\in {\mathbb{R}}^{D_{in}^s},{\mathbf{\Sigma }}^s\in {\mathbb{R}}^{D_{in}^s\times D_{in}^s}$ 。然后，公式11变为：

KaTeX parse error: Undefined control sequence: \label at position 495: …W}^s_{i,:})^T. \̲l̲a̲b̲e̲l̲{eq:obj-weight3…

这里，公式12是得到的 $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ 的代理。在实践中，使用给定的校准数据集来估计经验值 ${\hat{\mathbf{\mu }}}^s$ 和 ${\hat{\mathbf{\Sigma }}}^s$ 。请注意，对于所有输出通道， ${\hat{\mathbf{\mu }}}^s$ 和 ${\hat{\mathbf{\Sigma }}}^s$ 是共享的，只需进行一次计算。

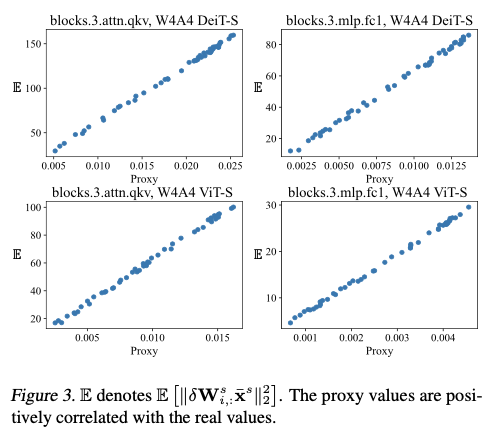
图3展示了代理与 $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ 之间的关系。可以看出，所提出的代理与真实值成比例，证明了其可信度。

使用代理的计算复杂度为 $O((D_{in}^s{)}^2)$ ，而 $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ 的复杂度为 $O(N{D}_{in}^s)$ ，其中 $N>>D_{in}^s$ 。因此，该代理可以作为一个低成本的目标，用于求解 $\delta {\mathbf{W}}_{i,:}^s$ 。如表1所示，将方程12作为MIPQ的目标将时间成本从约130小时降低到约10小时。然而，由于当前开源的MIPQ实现仅支持CPU，无法充分利用GPU的能力，这样的成本仍然是适度的。接下来将介绍Rounding Refinement，一种支持GPU的方法，利用代理的梯度更快地调整 $\delta {\mathbf{W}}_{i,:}^s$ 。

• Rounding Refinement

首先，使用最接近取整策略初始化 $\delta {\mathbf{W}}_{i,j}^s$ 。此时， $\delta {\mathbf{W}}_{i,j}^s$ 要么等于 $\delta {\mathbf{W}}_{i,j}^{s\downarrow }$ ，要么等于 $\delta {\mathbf{W}}_{i,j}^{s\uparrow }$ 。然后，目标是确定一个索引集合 $\mathcal{S}$ ，该集合包含需要修改的元素的索引集合，其取整方向被颠倒：

KaTeX parse error: Undefined control sequence: \label at position 288: …n \mathcal{S}. \̲l̲a̲b̲e̲l̲{eq:obj-weight6…

为了确定 $\mathcal{S}$ ，首先对代理（公式12）相对于 $\delta {\mathbf{W}}_{i,:}^s$ 求导。

KaTeX parse error: Undefined control sequence: \label at position 352: …l{\Sigma}^s) . \̲l̲a̲b̲e̲l̲{eq:obj-weight4…

只选择梯度符号相同的元素，因为这才是允许颠倒的唯一方式。例如，当 $\delta {\mathbf{W}}_{i,j}^s=\delta {\mathbf{W}}_{i,j}^{s\downarrow }$ 时，仅当 ${\mathbf{G}}_{\delta {\mathbf{W}}_{i,j}^s}$ 与 $\delta {\mathbf{W}}_{i,j}^s$ 具有相同的符号时，才能将其替换为 $\delta {\mathbf{W}}_{i,j}^{s\uparrow }$ 。因此，索引集合 $\mathcal{S}$ 定义为：

KaTeX parse error: Undefined control sequence: \label at position 286: …R}^{D_{in}^s}. \̲l̲a̲b̲e̲l̲{eq:obj-weight5…

这里， $topk\_index$ 返回前 $\mathrm{k}$ 个元素的索引， $1(\cdot )$ 对于非负输入返回1，对负输入返回0， $|\cdot |$ 返回输入的绝对值。

在获得 $\mathcal{S}$ 后，通过公式13进行颠倒。上述过程会迭代，直到调整后的 $\delta {\mathbf{W}}_{i,:}^s$ 引发更大的代理值或达到最大迭代次数。在获得 $\delta {\mathbf{W}}_{i,:}^s$ 后，量化可以通过 ${\bar{\mathbf{W}}}_{i,:}^s={\mathbf{W}}_{i,:}^s+\delta {\mathbf{W}}_{i,:}^s$ 完成。然后，将 ${\bar{\mathbf{W}}}_{i,:}^s$ 添加到量化权重集合中。Rounding Refinement的整体过程在算法1的第7行到第18行中给出。如表1所示，Rounding Refinement通过 $150\times$ 的成本显著减少了时间开销，从10小时减少到4分钟，同时可接受的准确性损失。

• Ridge Regression

在Rounding Refinement之后，建议用 $\delta {\mathbf{W}}_{i,:}^{r\ast }$ 调整 ${\mathbf{W}}_{i,:}^r$ ，以进一步抵消 $\mathbb{E}\left[\Vert \delta {\mathbf{W}}_{i,:}^s{\bar{\mathbf{x}}}^s{\Vert }_2^2\right]$ ，从而得到以下目标：

KaTeX parse error: Undefined control sequence: \label at position 224: …2, \end{split} \̲l̲a̲b̲e̲l̲{eq:obj-weight7…

其中， ${\lambda }_2$ 是一个超参数，用于控制正则化项 ${\lambda }_2\Vert \delta {\mathbf{W}}_{i,:}^{r\ast }{\Vert }_2^2$ 的强度。公式16的最小化形成了岭回归问题，解决方案定义为：

KaTeX parse error: Undefined control sequence: \label at position 266: …}. \end{split} \̲l̲a̲b̲e̲l̲{eq:obj-steptwo…

在实践中，通过使用 $\frac{1}{N}{\sum }_n^N{\bar{\mathbf{x}}}_n^r{\bar{\mathbf{x}}}_n^{sT}$ 和 $\frac{1}{N}{\sum }_n^N{\bar{\mathbf{x}}}_n^r{\bar{\mathbf{x}}}_n^{rT}$ 来估计 $\mathbb{E}\left[{\bar{\mathbf{x}}}^r{\bar{\mathbf{x}}}^{sT}\right]$ 和 $\mathbb{E}\left[{\bar{\mathbf{x}}}^r{\bar{\mathbf{x}}}^{rT}\right]$ 。随后， ${\mathbf{W}}_{i,:}^r={\mathbf{W}}_{i,:}^r+\delta {\mathbf{W}}_{i,:}^{r\ast }$ 以减小误差。目前， ${\mathbf{W}}_{i,:}^r$ 仍然保持为全精度，并将在下一次迭代中处理。该过程持续进行，直到所有权重被准确量化。所提出的Rounding Refinement和Ridge Regression共同形成了Wqer，其整体过程在算法1中给出。在实践中，对多个输出通道并行执行Wqer。

Experiments

---

 
 
 

如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】