SVM详细推导（包含dual-form的推导过程）

线性可分

SVM关于二分类问题的算法，也就是将一组数据线性的分成两类，什么是线性的分成两类呢？就是像图（1）这样的数据用一条线可以进行一分为二。

像图（2）这种数据使用一条线是分不开的，那么这种数据就成为线性不可分的数据，对于这种数据SVM就没有办法了吗？当然有办法了不然也不会在早期这么流行的。

SVM

margin的概念

假设现在有这样一组数据， D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) . . . ( x n , y n ) } ， D=\{(x_1,y_1),(x_2,y_2),(x_3,y_3)...(x_n,y_n)\}， D={ (x1​,y1​),(x2​,y2​),(x3​,y3​)...(xn​,yn​)}，其中$x$表示数据，$y$表示对应的标签， y ∈ { 1 , − 1 } y\in\{1,-1\} y∈{ 1,−1}现在用图（3）来表示：

现在用一条线来区分，假设这条线为：$W^T{x}_i+b$来表示，也就是说$W^T{x}_i+b\ge 0$时$，y=1，$$W^T{x}_i+b\le 0$时$，y=-1$也可以用$(W^T{x}_i+b)\cdot y\ge 0$来表示。

图（4）表示的是我们使用了 ①，②和③条作为决策边界来进行将数据分类，从图中我们明显看到这三条线都成功的将数据进行了分类，但是那个分类的最好呢，答案是②，①和③距离数据太近了，有可能造成误判，并且很容易过拟合，对于②来说我们离数据的距离比较远，增加一些噪音的话也是可以保证分类的正确性。

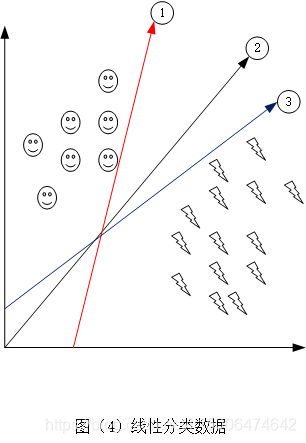
因此我们通常把这个距离叫做margin。我们的分类器离数据的距离越大越好，所以margin的目标就是最大化margin。

margin的计算

那么margin该怎么计算呢？由图（5）我们可以看到$Wx+b=0$表示决策边界另外我们设置两条线$W^{T}x+b=1$和$W^{T}x+b=-1$表示分别表示数据集中最外围，所以margin就是这两条线之间的距离，这里因为有$W和b$的存在，所以我们将其设置为1和-1

假设$x_{+}$表示$W^{T}x+b=1$上的点，$x_{-}$表示$W^{T}x+b=-1$上的点，$margin=|x_{+}-x_{-}|$,$w$表示与这三条线垂直的方向

我们可以得到三个公式：
$\{\begin{array}{l}{W}^T{x}_{+}+b=1①\\ W^T{x}_{-}+b=-1②\\ x_{+}=x_{-}+\lambda w③\end{array}$

现在我们来计算$margin$将③式代入①中得：
$W^T(x_{-}+\lambda w)+b=1$

$W^T{x}_{-}+W^T\lambda w+b=1④$
将④-②得
$\lambda W^{T}w=2$

$\lambda =\frac{2}{W^{T}w}$

$margin=|x_{+}-x_{-}|$由③可知：$margin=|\lambda w|=|\frac{2}{W^{T}w}\cdot w|=|\frac{2}{W^T}|$

所以最后
$margin=|\frac{2}{W^T}|$

SVM的目标函数

svm的目标就是最大化$margin$也就是：
$maxmize\frac{2}{||W^T||}$

$st:W^{T}x+b\ge 1if:y=1$

$W^{T}x+b\le -1if:y=-1$

我们来简单改变一下公式：

$minemize||W^T|{|}^2$

$st:W^{T}x+b\ge 1if:y=1$

$W^{T}x+b\le -1if:y=-1$

把条件整合一下

$minemize||W^T||$