1. KL散度
KL K L 散度又称为相对熵,信息散度,信息增益。 KL K L 散度是是两个概率分布P和Q 差别的非对称性的度量。 KL K L 散度是用来 度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下,P表示数据的真实分布,Q表示数据的理论分布,模型分布,或P的近似分布。
定义如下:
因为对数函数是凸函数,所以 KL K L 散度的值为非负数。
有时会将 KL K L 散度称为 KL K L 距离,但它并不满足距离的性质:
| 1. KL散度不是对称的: KL(A,B) K L ( A , B ) ≠ ≠ KL(B,A) K L ( B , A ) |
|---|
| 2. KL散度不满足三角不等式: KL(A,B) K L ( A , B ) > > |
|---|
2. JS散度(Jensen-Shannon)
JS J S 散度度量了两个概率分布的相似度,基于 KL K L 散度的变体,解决了KL散度非对称的问题。一般地, JS J S 散度是对称的,其取值是0到1之间。定义如下:
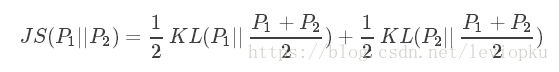
KL K L 散度和 JS J S 散度度量的时候有一个问题:
| 如果两个分配P,Q离得很远,完全没有重叠的时候,那么KL散度值是没有意义的,而JS散度值是一个常数。这在学习算法中是比较致命的,这就意味这这一点的梯度为0。梯度消失了。 |
|---|
3. Wasserstein距离
Wasserstein
W
a
s
s
e
r
s
t
e
i
n
距离度量两个概率分布之间的距离,定义如下:
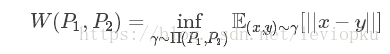
Π(P1,P2)
Π
(
P
1
,
P
2
)
是
P1
P
1
和
P2
P
2
分布组合起来的所有可能的联合分布的集合。对于每一个可能的联合分布γ,可以从中采样
(x,y)∼γ
(
x
,
y
)
∼
γ
得到一个样本x和y,并计算出这对样本的距离||x−y||,所以可以计算该联合分布
γ
γ
下,样本对距离的期望值
E(x,y)∼γ[||x−y||]
E
(
x
,
y
)
∼
γ
[
|
|
x
−
y
|
|
]
。在所有可能的联合分布中能够对这个期望值取到的下界
infγ
i
n
f
γ
∼
Π(P1,P2)
Π
(
P
1
,
P
2
)
E(x,y)
∼γ[||x−y||]
∼
γ
[
|
|
x
−
y
|
|
]
就是Wasserstein距离。
直观上可以把 E(x,y)∼γ[||x−y||] E ( x , y ) ∼ γ [ | | x − y | | ] 理解为在 γ γ 这个路径规划下把土堆P1挪到土堆P2所需要的消耗。而 Wasserstein W a s s e r s t e i n 距离就是在最优路径规划下的最小消耗。所以 Wesserstein W e s s e r s t e i n 距离又叫Earth-Mover距离。
Wessertein距离相比KL散度和JS散度的优势在于:
| 即使两个分布的支撑集没有重叠或者重叠非常少,仍然能反映两个分布的远近。而JS散度在此情况下是常量,KL散度可能无意义。 |
|---|
转载自:
《KL散度、JS散度、Wasserstein距离》








 本文介绍了三种用于衡量概率分布差异的方法:KL散度、JS散度及Wasserstein距离。KL散度是一种非对称性度量,而JS散度改进了这一特性,Wasserstein距离则能在分布支撑集不重叠时仍有效度量差异。
本文介绍了三种用于衡量概率分布差异的方法:KL散度、JS散度及Wasserstein距离。KL散度是一种非对称性度量,而JS散度改进了这一特性,Wasserstein距离则能在分布支撑集不重叠时仍有效度量差异。
















 238
238

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








