基于labview的信号采集与频率计算2

优快云话题挑战赛第2期
参赛话题：学习笔记

数据采集得到的信号波形是时域的数字信号，利用离散傅里叶变换将其转换到频域表示，便得到该数字信号的频谱信息，再经相应运算，也可得到被测信号的频率。
1）离散傅里叶变换（DFT）
频域算法的理论基础是傅里叶变换。对数字信号的傅里叶变换，称为离散傅里叶变换（DFT）。DFT是指，对于一个用x（n）（n=0，1，2，…，N－1）表示的数字信号序列，其离散数据点的个数设为N，变换到频域后用X（k）来表征，则该数字信号序列的DFT计算式如下：

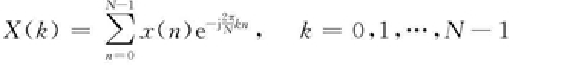
其中，x（n）为时域采样数字信号序列；X（k）表征x（n）变换到频域的复数形式的幅值序列（频谱值）；N为时域采样点（值）的数量；n=0，1，2，…，N－1，对应采样点（值）的编号；k=0，1，…，N－1，是幅值频谱谱线的编号。

2）快速傅里叶变换（FFT）
FFT是实现DFT的快速算法。LabVIEW中有现成的函数可以实现它，其图标如图15.13所示。接下来，就调用此函数来对一个输入信号进行FFT。

在进行FFT时，提到的非整周期采样是第一类，即采集到被测信号波形的周期数不是整数。这是因为，对于信号x（n），若其真实频率为f，采样率为Fs，采样样本数为#s，经过FFT变换到频域，这时得到的是一根根离散的谱线，两两相邻谱线之间的频率间隔d f=Fs/#s，如果f/d f=#sf/Fs等于整数的话，则f恰好落在其中的一根谱线上。而f/d f=#sf/Fs=m反映到时域中，就是采集到信号波形的周期数。具体推导过程如下：#sf/Fs=（#s/Fs）f，#s/Fs=Tsum为被测信号波形的总的时间长度，f=1/T为被测信号的频率（即周期T的倒数），所以#sf/Fs=Tsum/T，也就是说在时域中的含义是采集到信号波形的周期数

过零插值法VI的程序框图

峰值多周期平均法程序框图

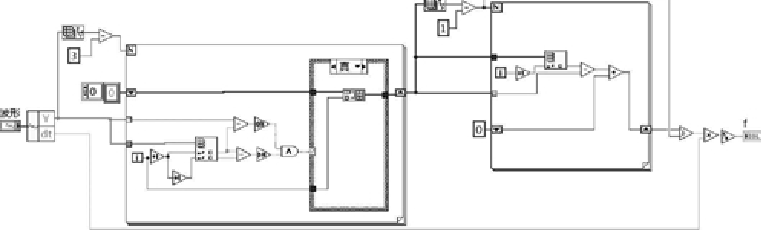
三点法VI的程序框图

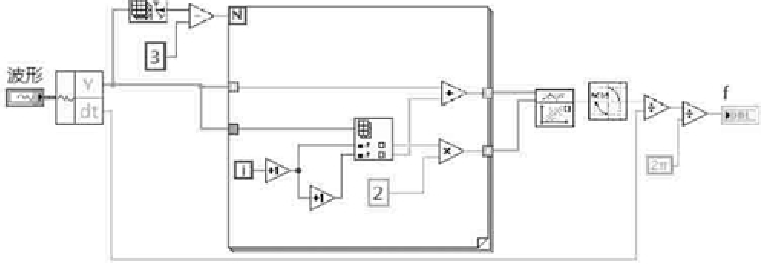
自相关算法VI的程序框图

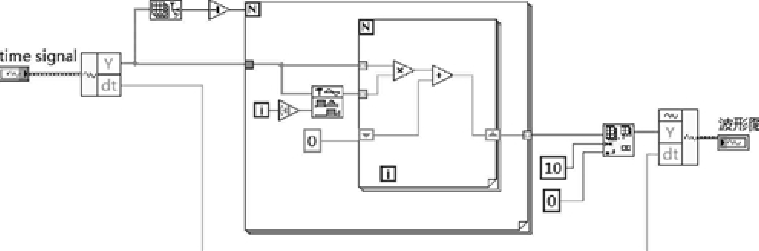
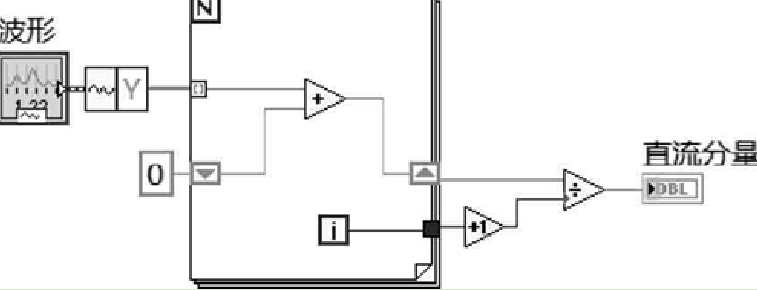
计算直流分量VI的程序框图