来源:Python数据之道
作者:Peter
整理:Lemon
8个知识点,图解K-Means算法
之前,公众号分享了关于 KNN算法 的介绍,今天,我们来学习下另一个经典的算法:K-means算法。
本文中介绍的是一种常见的无监督学习算法,名字叫做 K 均值算法:K-Means算法。
K-Means算法在无监督学习,尤其是聚类算法中是最为基础和重要的一个算法。它实现起来非常简单。聚类效果也很不错的,因此应用非常广泛。
本文将会从以下 8 个方面进行详细的讲解:
算法思想
无监督学习
在正式介绍 K-Means 算法之前,我们先解释一下无监督学习。用一句很通俗的话来解释:
是否有监督(supervised),我们只需要看输入的数据是否有标签
输入的数据如果带有标签,则是有监督学习,比如 KNN算法(K近邻)就是监督学习的典型算法;如果没有标签,则认为是无监督学习,比如本文中即将介绍的 K-Means算法
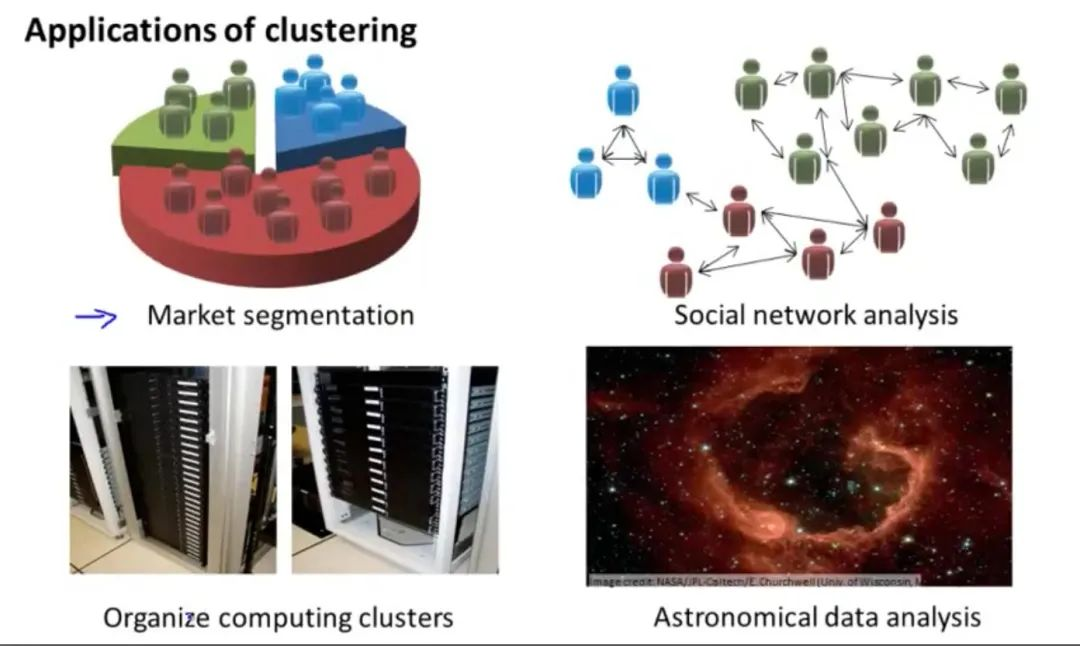
我们看看无监督学习聚类算法的应用:
市场分割
社交网络分析
组织计算机集群
星系的形成
算法思想
K-Means 聚类算法是一种迭代求解的聚类分析算法。算法思想是:我们需要随机选择 K 个对象作为初始的聚类中心,然后计算每个对象和各个聚类中心之间的距离,然后将每个对象分配给距离它最近的聚类中心。
聚类中心及分配给它们的对象就代表着一个聚类。每分配一个样本,聚类的中心会根据聚类中现有的对象被重新计算。此过程将不断重复,直至满足设置的终止条件。
算法步骤
K-Means 算法的具体步骤如下:
首先我们需要确定一个k值(随机),即我们希望数据经过聚类得到k个不同的集合;
从给定的数据集中随机选择K个数据点作为质心;
对数据集中的每个点计算其与每一个质心的距离(比如欧式距离);数据点离哪个质心近,就划分到那个质心所属的集合;
第一轮将所有的数据归号集合后,一共有K个集合,然后重新计算每个集合的质心;
如果新计算出来的质心和原来的质心之间的距离小于某一个设置的阈值,则表示重新计算的质心的位置变化不大,数据整体趋于稳定,或者说数据已经收敛。在这样的情况下,我们认为聚类效果已经达到了期望的结果,算法可终止;
反之,如果新质心和原来质心的距离变化很大,需要重复迭代3-5步骤,直至位置变化不大,达到收敛状态。
图解K-Means
具体步骤
1、给定需要进行聚类划分的数据集
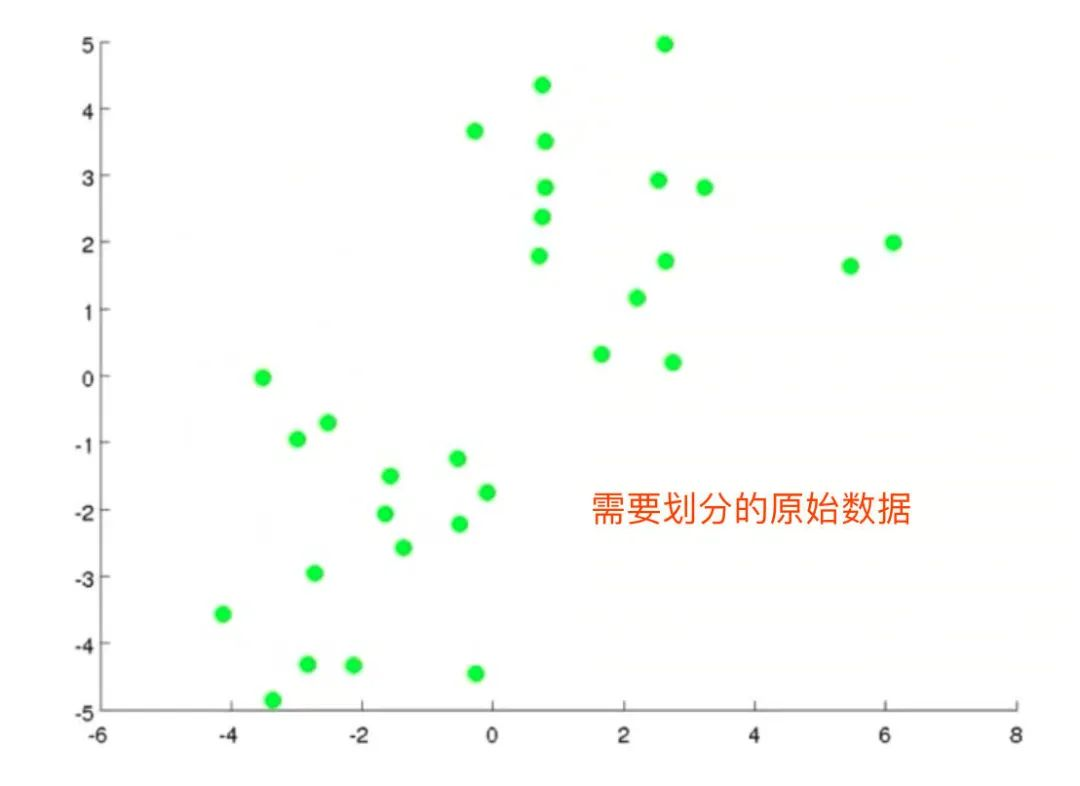
2、随机选择2个聚类中心(K=2)
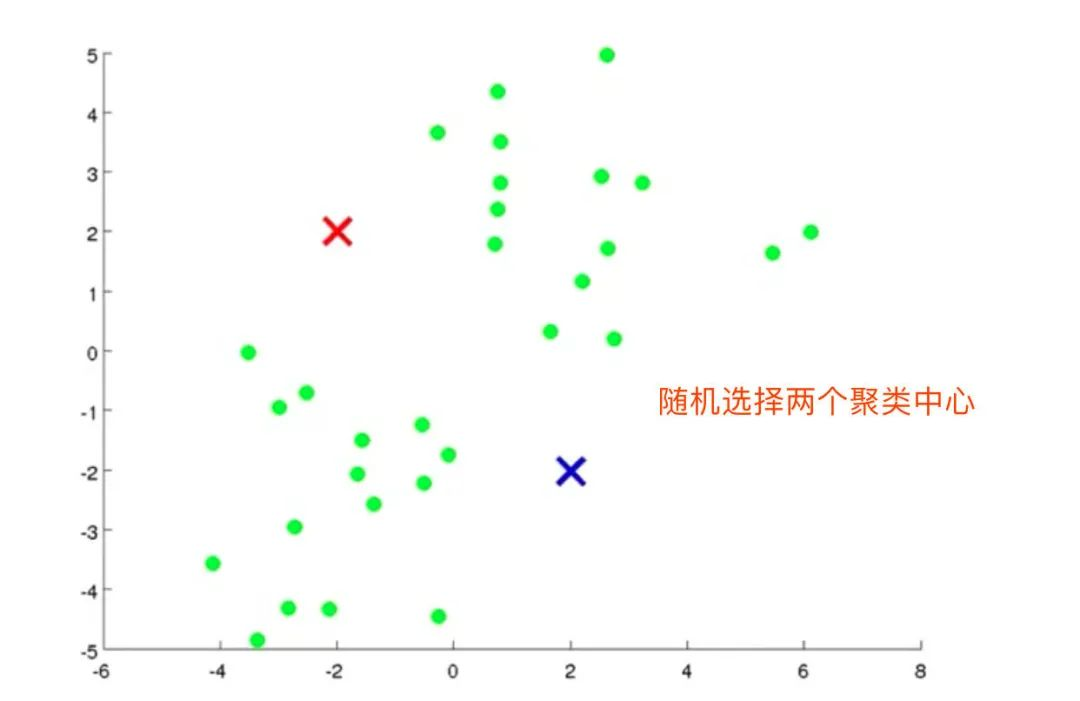
3、计算每个数据点到质心的距离,并将数据点划分到离它最近的质心的类中
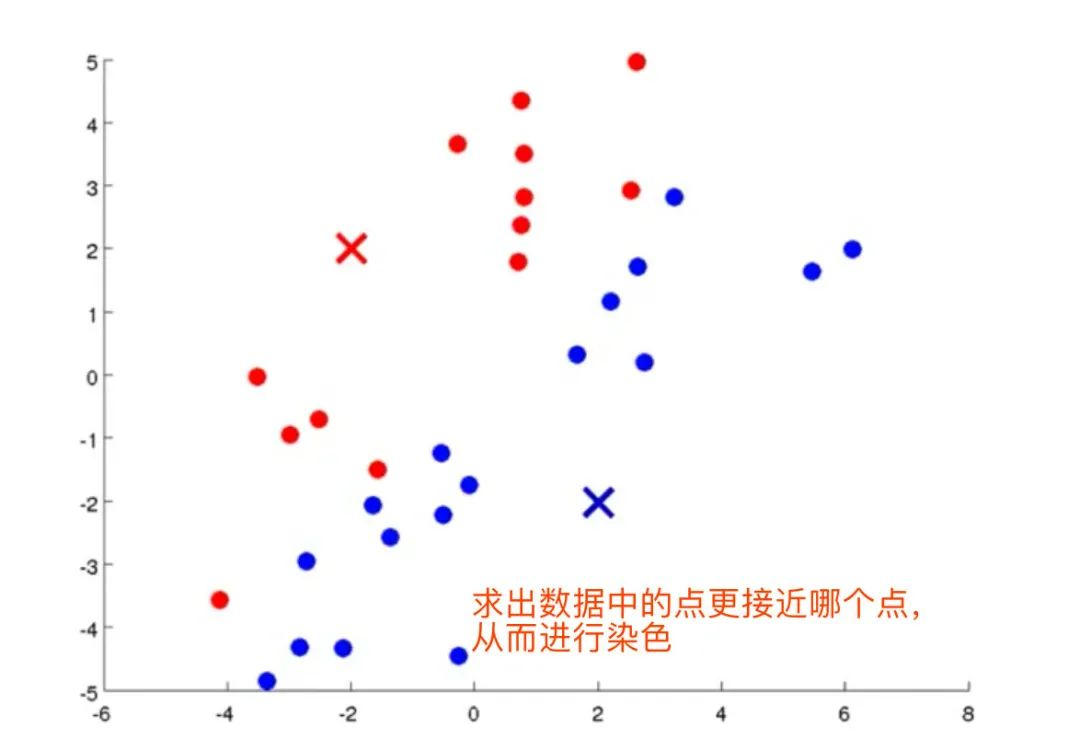
4、计算2个数据集的各自的质心(红点、蓝点的均值),将聚类中心移动到均值处,变成新的聚类中心
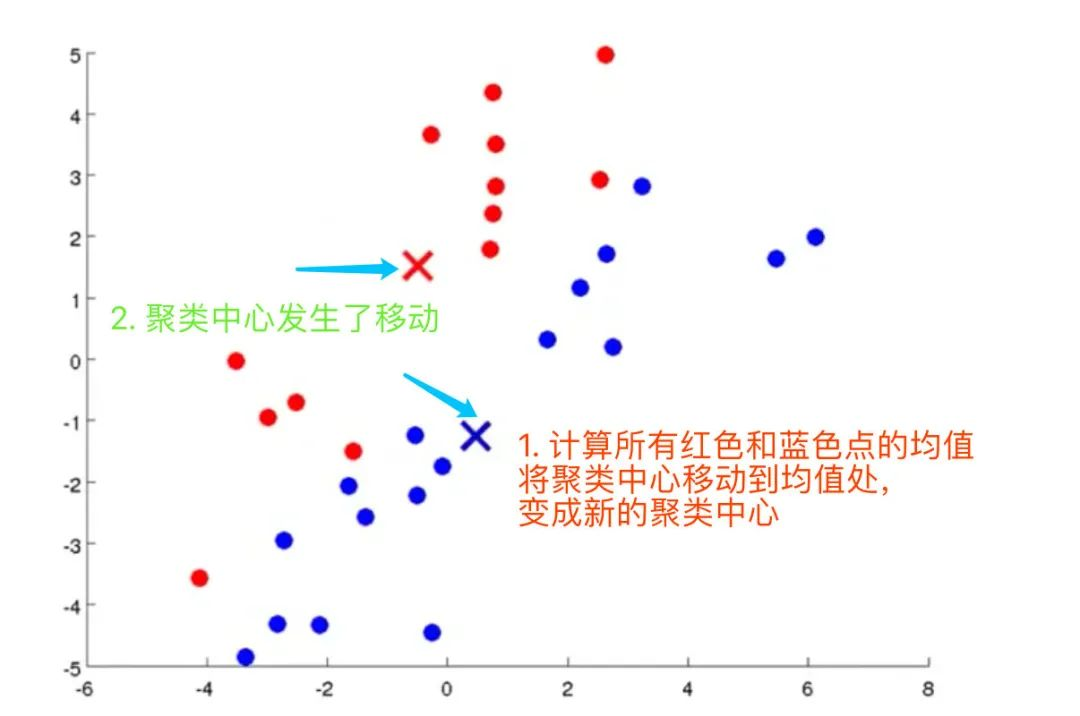
5、找到新的聚类中心。如果
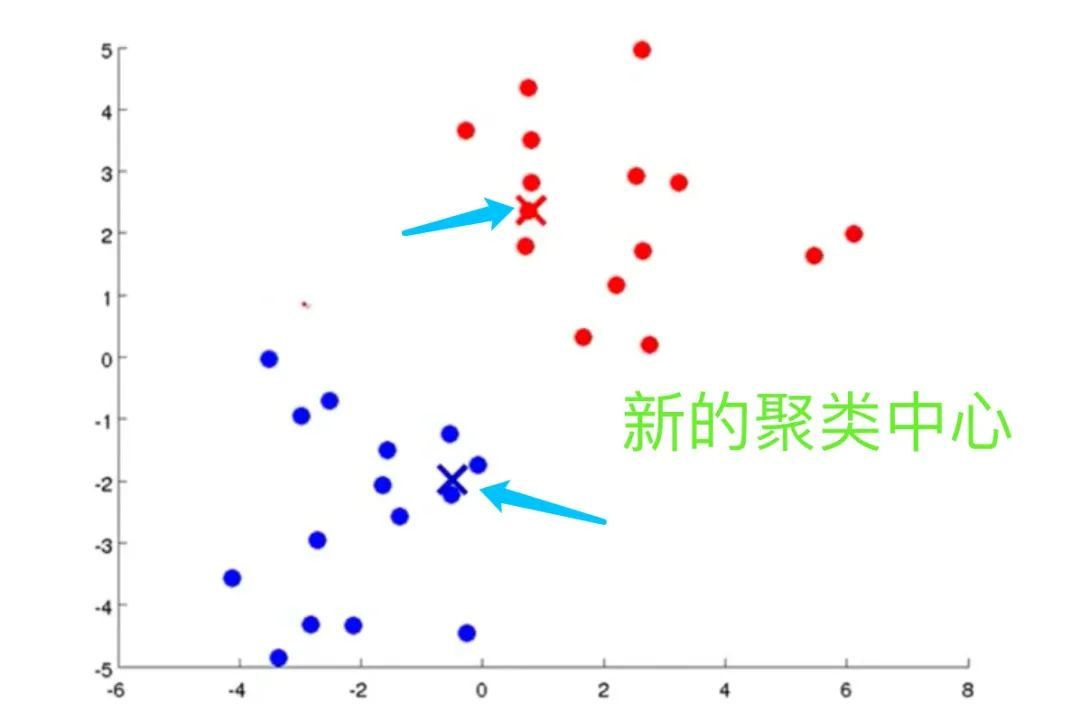
完整过程
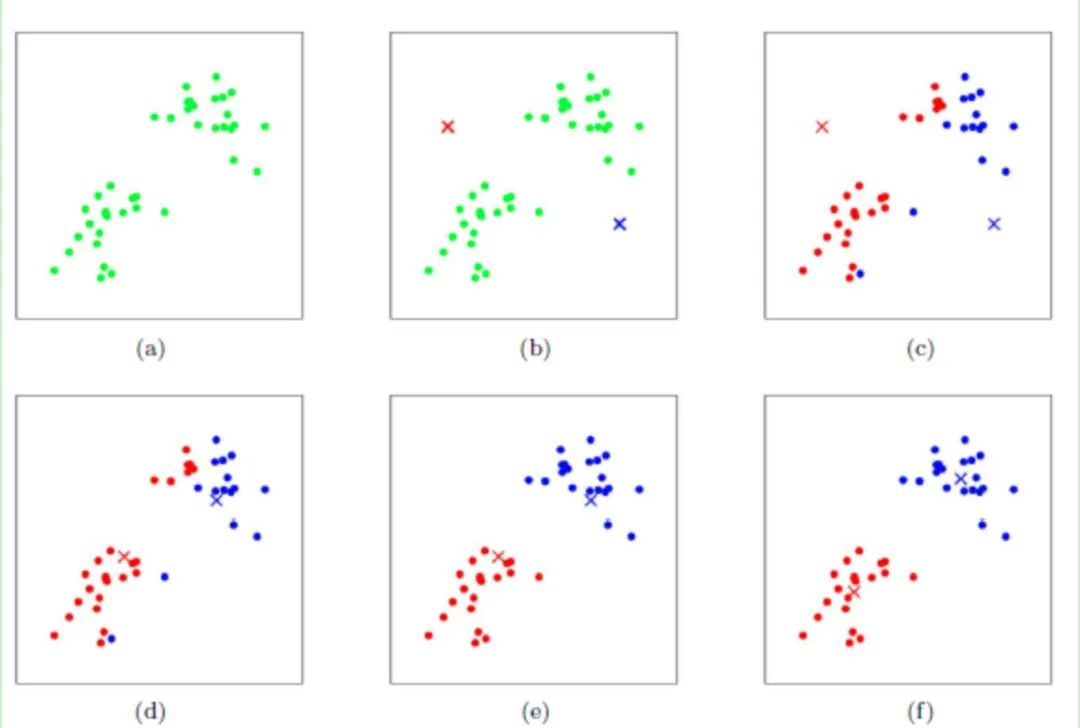
在上面的过程中我们假设k=2。在图b中我们随机选择了两个类所对应的质心,也就是图中蓝色和红色质心;
分别求出样本中每个点到这两个质心的距离,并且将每个样本所属的类别归到和该样本距离最小的质心的类别,得到图c,也就是第一轮迭代后的结果;
我们对c图中的当前标记为红色和蓝色的点分别求出其新的质心,得到了图d,此时质心的位置发生了改变;
图e和图f重复了图c和图d的过程,即将所有点的类别标记为距离最近的质心的类别并求新的质心;
一般的,
K-Means算法需要运行多次才能达到图f的效果。
注:以上图形来自吴恩达老师在机器学习视频的讲解截图
k值选择
k值决定了我们将数据划分成多少个簇类。k个初始化的质心的位置选择对最后的聚类结果和整个大代码的运行时间都有非常大的影响。因此需要选择合适的k个质心
一般k值是通过先验知识来选取的。如果没有什么先验知识,我们可以通过交叉验证的方式来选择一个合适的k值。
距离问题
在机器学习中,我们常用的距离有以下几种:
1、两个集合之间的 的 距离定义为:
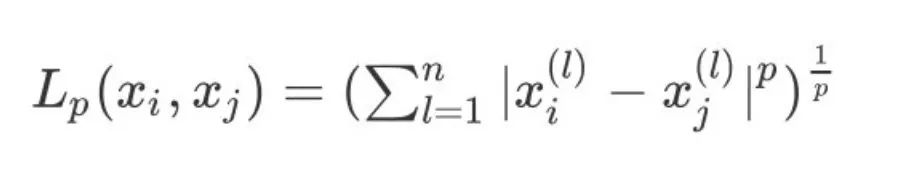
2、当 p=1 则表示为曼哈顿距离:
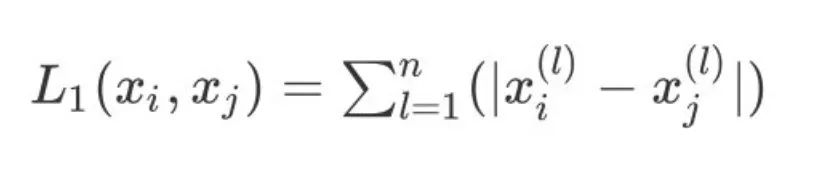
3、当 p=2 则表示为我们常用的欧式距离:
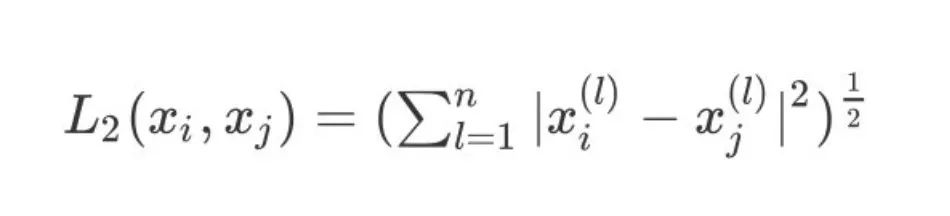
4、当p趋于无穷时,表示为切比雪夫距离,它是各个坐标距离的最大值:
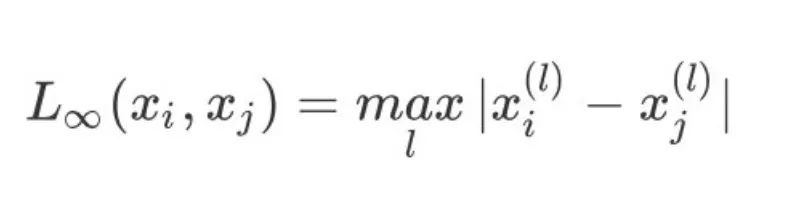
在K-Means算法中一般采用的是欧式距离
算法优缺点
优点
原理很简单,实现起来也是非常容易,算法收敛速度也很快
聚类效果优,可解释性强。当数据最终收敛之后,我们最终能够很清晰的看到聚类的效果
约束条件少。算法中需要控制的参数只有簇数k。通过对k的不断调节才能得到最好的聚类效果
缺点
k值的选取不好把握,很多情况下K值的估计是非常困难的,有时候通过交叉验证来获取。
迭代的方法得到的结果只能是局部最优解,而不能得到全局最优解。
对噪音和异常点很敏感。异常点对质心的确定影响很大的。可以用来检测异常值。
Python实现K-Means
下面讲解一种利用 Python 实现 k-means 算法的代码:
import numpy as np
import pandas as pd
import random # 随机模块
import re
import matplotlib.pyplot as plt
# 导入数据
def loadDataSet():
dataset = np.loadtext("user/skl/cluster/dataset.csv") # 个人文件路径
return dataset # 返回数据集
# 绘图函数
def show_fig():
dataset = loadDataSet() # 导入数据
fig = plt.figure() # 确定画布
ax = fig.add_subplot(111) # 一个子图
ax.scatter(dataset[:,0], dataset[:,1]) # 传入绘图数据
plt.show()
# 定义欧式距离公式
# 两个向量间的欧式距离公式:[(x_1 - x_2)^2 + (y_1 - y_2)^2 + (x_n - y_n)^2]
def calcudistance(vec1,vec2): # 传入两个向量
return np.sqrt(np.sum(np.square(vec1 - vec2))) # 向量相减在平方,最后再求和
# 初始化质心
def initCentroids(dataset, k):
# 初始化执行;dataset是传入的数据
# k:选择分类簇的个数
dataset = list(dataset) # 数据列表化
return random.sample(dataset,k) # 随机选取k的模块
# 计算每个数据点和质心的距离,并归属到距离最小的类别中
def minDisctance(dataset, centroidList): # 传入数据集和选取的质心列表
clusterDict = dict() # 保存簇类结果
k = len(centroidList) # 质心列表的长度:总共多少个质心表示分成多少类
for item in dataset: # 原始数据中的每个元素
vec1 = item # 数据中的向量
flag = -1 # 标志位
minDis = float("inf") # 初始化为无穷大值
for i in range(k):
vec2 = centroidList[i] # 取出第i个质心
distcance = calcudistance(vec1, vec2) # 计算欧式距离
if distance < minDis:
minDis = distance # 如果算出来的实际距离小于最小值的初始值,则将真实值distance赋值给最小值(更新最小值)
flag = i # 循环结束时,flag保存与当前item最近的簇标记
if flag not in clusterDict.keys():
clusterDict.setdefault(flag,[])
clusterDict[flag].append(item) # 加入到相应的簇类中
return clusterDict # 不同的类别
# 重新计算质心
def getcentroids(clusterDict):
# 重新计算k个质心
centroidList = [] # 质心空列表
for key in clusterDict.keys(): #
centroid = np.mean(clusterDict[key], axis=0) # 现有数据点的平均值
centroidList.append(centroid)
return centroidList # 得到新的质心
# 计算均方误差
def getVar(centroidList, clusterDict):
# 将簇类中各个向量和质心的距离累加求和
sum = 0.0 # 初始值
for key in clusterDict.keys(): # 簇类中的键
vec1 = centroidList[key] # 取出某个质心
distance = 0.0 # 距离初始化值
for item in clusterDict[key]: # 簇类的键
vec2 = item
distance += calcudistance(vec1, vec2) # 求距离
sum += distance # 累加
return sum
# 显示簇类
def showCluster(centroidList, clusterDict):
# 显示簇类结果
color_mark = ["or","ob","og","ok","oy","ow"]
centroid_mark = ["dr","db","dg","dk","dy","dw"]
for key in clusterDict.keys():
plt.plot(centroidList[key][0], centroidList[key][1], centroidMark[key],markersize=12) # 质心点
for item in clusterDict[key]:
plt.plot(item[0],item[1],colorMark[key])
plt.show()
# 主函数
def main():
dataset = loadDataSet() # 导入数据
centroidList = initCentroids(dataset,4) # 质心列表
clusterDict = minDistance(dataset, centroidList) # 簇类的字典数据
newVar = getVar(centroidList, clusterDict) # 质心和簇类中数据得到新的误差
oldVar = 1 # 当两次聚类的误差小于某个值时,说明质心基本稳定
times = 2
while abs(newVar - oldVar) >= 0.00001: # 当新旧误差的绝对值小于某个很小的值
centroidList = getCentroids(clusterDict) # 得到质心列表
oldVar = newVar # 将新的误差赋值给旧误差
newVar = getVar(centroidList, clusterDict) # 新误差
times += 1
showCluster(centroidList, clusterDict) # 显示聚类结果
if __name__ == "__main__":
show_fig()
main()
延伸学习
传统的 K-Means 算法存在一些缺陷,比如K值的选取不是很好把握、对异常数据敏感等,于是提出了很多在其基础上改进的聚类算法:
1、K-Means++(初始化优化)
针对K-Means算法中随机初始化质心的方法进行了优化
2、elkan K-Means(距离优化)
在传统的 K-Means 算法中,在每轮迭代中我们都需要计算所有的样本点到质心的距离,这样是非常耗时的。
elkan K-Means算法利用:两边之和大于等于第三边,以及两边之差小于第三边的三角形性质,来减少距离的计算。
3、Mini Batch K-Means算法(大样本优化)
在传统的K-Means算法中,要计算所有的样本点到所有的质心的距离。现在大数据时代,如果样本量非常大,传统的算法将会非常耗时。
Mini Batch K-Means 就是从原始的样本集中随机选择一部分样本做传统的 K-Means 。这样可以避免样本量太大的计算难题,同时也加速算法的收敛。当然,此时的代价就是我们最终聚类的精度会降低一些。
为了增加算法的准确性,我们一般会多跑几次 Mini Batch K-Means 算法,用得到不同的随机样本集来得到聚类簇,选择其中最优的聚类簇。
参考资料
1、李航老师—《统计学习方法》一书
2、吴恩达老师—《机器学习》视频
3、刘建平老师—博客:https://www.cnblogs.com/pinard/
作者简介
Peter,硕士毕业僧一枚,从电子专业自学Python入门数据行业,擅长数据分析及可视化。喜欢数据,坚持跑步,热爱阅读,乐观生活。个人格言:不浮于世,不负于己
个人站点:www.renpeter.cn,欢迎常来小屋逛逛
本文来自公众号读者投稿,欢迎各位童鞋向公号投稿,点击下面图片了解详情!
---------End---------

公众号后台回复「微信群」,将邀请加入读者交流群。

????分享、点赞、在看,给个三连击呗!????




 本文详细介绍了K-Means算法,包括算法思想、步骤、优缺点,以及Python实现。K-Means是一种无监督学习的聚类算法,通过迭代寻找数据的最佳分组。文章还探讨了k值选择、距离计算和算法的优化版本。
本文详细介绍了K-Means算法,包括算法思想、步骤、优缺点,以及Python实现。K-Means是一种无监督学习的聚类算法,通过迭代寻找数据的最佳分组。文章还探讨了k值选择、距离计算和算法的优化版本。



















 1468
1468

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








