机器学习
李宏毅老师的ML课程的笔记学习
机器学习就是让机器去寻找一个函数(Function),这个函数具备这样的能力,对于相对应地输入可以获得我们想要的输出,例如Speech Recognition语音辨识,我们把我们说的话作为输入,我们希望机器能找到一个Function,该Function可以输出这个说的话的文字内容。又比如Image Recognition图片辨识,我们希望机器能找到一个Function,对于输入的一张图片(比如猫),可以输出该图片是什么(猫)。
Regression:The function outputs a scalar机器要找一个Function,这个Function输出是一个数,这样的机器学习的任务我们称为Regression,比如预测明天pm2.5的数值
Classification:Given options(classes),the function outputs the correct one.给出一些classess(类别),机器要找一个Function,这个Function能从我们设定好的选项中,选择一个输出。比如从检测一个邮件是不是垃圾邮件。输入是一个邮件,输出我们设定了yes/no,机器要从中选出yes或者no
Regression和Classification是机器学习中的两大主要任务,除了这个两个任务以外呢,还有一个structured learning让机器学会创造,比如创造一首歌,一篇文章
- 先设置一个未知参数的函数,也就是猜测一下这个函数长什么样子呢,比如假设一个线性函数 y = b + w x 1 y=b+wx_1 y=b+wx1,比如 y y y为明天会观看我youtube频道的人数, x x x为之前已经有的数据,这两个是已经知道的参数, b w bw bw为两个未知参数,这个带有未知参数的函数呢,我们就称之为模型Model, x x x为已知量,称为feature,w称为weight,b为bias
- 我们要定义一个东西Loss,这也是也是一个Function,这个函数的输入就是Model里面的未知量b,w,即 L ( b , w ) L(b,w) L(b,w),这个函数的输出是当我们找到一对(b,w)时,这对数值是好的还是不好的
- 我们找一对b和w,使得我们的Loss最小,采用Gradient Descent,也就是梯度下降算法,
梯度下降算法
但是呢,问题往往没有这简单,一般我们要找的方程并不是一条直线,而是一条有转折的直线,如图中红色线段所示。
那么我们要怎么表示这一条红色的线呢?我们可以将红色的线段(red curve)看作是一个常数(constant)+ 一些蓝色的曲线

我们将0,1,2,3这些线段相加,就能得到红色的线段。从上图可以得出,我们可以用常数加一堆蓝色的曲线来表示任意的有拐角的直线(包括曲线),那么问题来啦?我们怎么表示这一个蓝色的曲线呢?我们可以用
y
=
c
i
1
1
+
e
−
(
b
i
+
w
i
x
1
)
=
c
i
s
i
g
m
o
i
d
(
b
i
+
w
i
x
1
)
y=c_i\cfrac{1}{1 + e^{-(b_i+w_ix_1)}}=c_i sigmoid(b_i+w_ix_1)
y=ci1+e−(bi+wix1)1=cisigmoid(bi+wix1)

来逼近蓝色的曲线,对于之前的0,1,2,3这些线段我们怎么用sigmoid来表示呢?我们只需要取同的
c
1
,
b
1
,
w
1
c_1,b_1,w_1
c1,b1,w1来表示我们不同的sigmoid的函数就可以啦,而我们把0,1,2,3这些线段加起来呢,就得到式子
y
=
b
+
∑
i
c
i
s
i
g
m
o
i
d
(
b
i
+
w
i
x
1
)
y=b+\sum_ic_isigmoid(b_i+w_ix_1)
y=b+i∑cisigmoid(bi+wix1)
也就是将红色转折线看作是b加上一些sigmoid函数
如果我们用比较复杂的feature如
y
=
b
+
∑
j
w
j
x
j
y=b+\sum_jw_jx_j
y=b+∑jwjxj来表示
b
i
+
w
i
x
1
b_i+w_ix_1
bi+wix1可以得到
y
=
b
+
∑
i
c
i
s
i
g
m
o
i
d
(
b
i
+
∑
j
w
i
j
x
j
)
y=b+\sum_ic_isigmoid(b_i+\sum_jw_{ij}x_j)
y=b+i∑cisigmoid(bi+j∑wijxj)
为了直观,我们取j为1,2,3特征的编号,取i为1,2,3表示三个蓝色的function



上图就是对整个式子的拆解:向量x乘上矩阵w加上向量b得到向量r,在对r做sigmoid运算得到向量a,对a乘上向量c的转置,最后加上一个b就得到y。

x是我们的feature,而向量w,b,c,数字b全部拼起来,我们得到一个向量
θ
\theta
θ,表示未知的参数。至此我们完成了机器学习的第一步,找到了一个含有未知参数的function
y
=
b
+
c
T
σ
(
b
+
W
x
)
y =b + c^T \sigma( b + W x)
y=b+cTσ(b+Wx)
接下来我们要做第二步,找到Loss首先呢,Loss是一个对于未知参数而言的函数
L
(
θ
)
L(\theta)
L(θ),我们就是要找到一组未知的参数
θ
\theta
θ ,使得我们的Loss越小越好


不断的计算直到我们得到的
θ
\theta
θ是0向量(基本不可能,一般是你做到不想做了),
当然对于
s
i
g
m
o
i
d
sigmoid
sigmoid函数我可以用另外的函数来替换,也就是Rectified Linear Unit(ReLu)
c
m
a
x
(
0
,
b
+
w
x
1
)
c max(0,b+wx_1)
cmax(0,b+wx1)

两个ReLu的叠加就是最上面的函数样子。

将sigmoid换成ReLu呢要注意i的范围是2倍的,因为两个ReLu函数才能表示一个sigmoid函数。sigmoid和ReLu我们称为Activation function(激活函数)

当然我们还可以对sigmoid或者ReLu的操作多做几次。为了名字更高级一点,我们把sigmoid或者ReLu称为Neuron 神经元,做很多次的sigmoid或者RuLu操作我们称为Neural Network 神经网络
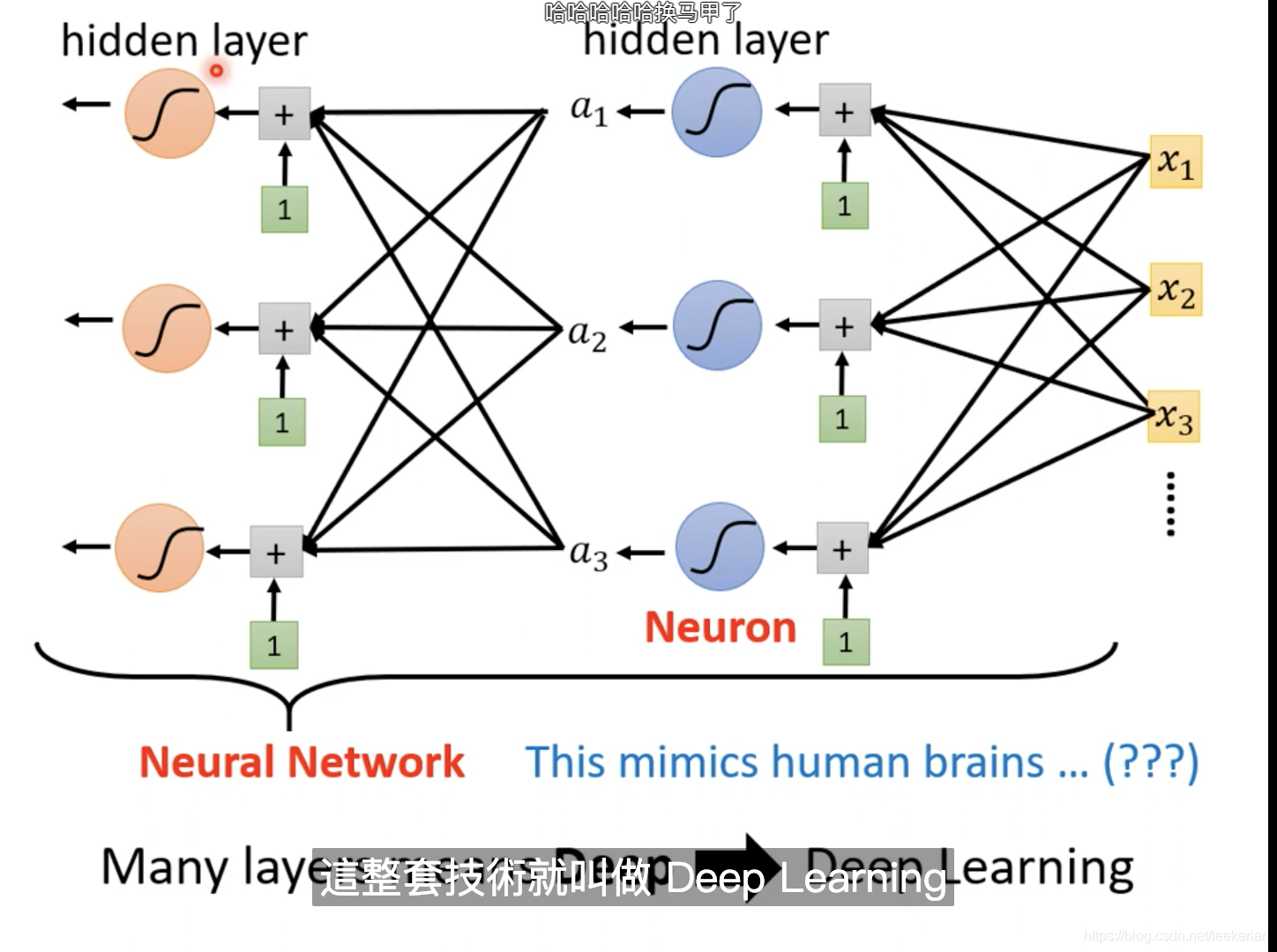
我们把每一排的Neural我们叫它一个Layer,也就是hidden layer,有很多的hidden layer我们也叫做deep,这套技术就叫做deep learning。
在随着layer的增加
在训练资料上变好,而预期资料上变差,这种现象我们称为Overfitting 过度拟合。

随着参数的不断update,但是发现我们的training loss不再下降,又或者是随着参数的不断update我们的training loss不再改变。过去往往认为我们走到了一个地方,这个地方的微分为0。也就是gradient为0的地方。最先想到的呢?也就是local minima(局部最优解),但是不是只有local minima的gradient为0,还有一种情况我们称为saddle point(鞍点)。所谓的saddle point:也就是指gradient为0,但是既不是local minima也不是local maxima的地方。
-
如何辨别是saddle point还是local minima?

虽然说我们不能知道 L ( θ ) L(\theta) L(θ)的形状,但是我们可以用泰勒公式来近似得表示。H是一个海森矩阵,里面存的是二次微分。
如果我们走到了一个 critical point,那么也就是说这个点的gradent为0,也就是中间的第二项为零。

这样我们就可以通过红色这一项来判断到底是:local minima,local maxma,saddle point
 那么怎么根据Hessian矩阵来是什么状态呢?
那么怎么根据Hessian矩阵来是什么状态呢?

根据我们小学二年级就学过的加法运算,我们只需要知道红色项的大小,就能得出 L ( θ ) L(\theta) L(θ)与 L ( θ ′ ) L(\theta') L(θ′)的关系,从而判断出是属于哪一种状态。但是对于for all v(也就是所有的v)这一个条件不太现实,所以有个更简便的方法去确认红色项的大小。我们可以通过矩阵的特征值eigen values来判断红色项的大小(矩阵的二次型)。
举例子如下:

如果我们找到的当前critical point是saddle point,Hession矩阵就可以告诉我们应该更新的方向。

我们假设 u u u是Hession矩阵的特征值所对应的特征向量, λ \lambda λ是矩阵的特征值,当 λ \lambda λ小于0的时候,我们可以得出红色矩形里的项小于0,也就是说 L ( θ ) L(\theta) L(θ)小于 L ( θ ′ ) L(\theta') L(θ′)也就说 L ( θ ) L(\theta) L(θ)的Loss更小,这是我们需要的方向,当然这个的前提条件是 θ − θ ′ = u \theta-\theta'=u θ−θ′=u,通过小学二年级就会的加减法,我们可以得出 θ = θ ′ + u \theta=\theta'+u θ=θ′+u,也就是说我们沿着u的方向更新,也就能让我们的Loss更小。所以问题就变成:当我们遇到一个saddle point的时候,我们只要找出负的特征向量和所对应的特征值。用特征向量去加 θ ‘ \theta‘ θ‘。但是在实际应用中不使用这个方法,因为计算Hession,还有二次微分的计算量比较大。 -
Batch and Momentum

Momentum:
我们不仅仅只根据我们算出的gradient的方向来更新我们下一步走的方向,而是根据算出来的gradient和上一次走的方向的两个向量的和来确定方向,m表示上一次走的方向。这样我们就能有一定的几率走出当前的local minima,从而走到更好的local minima的位置。

对于等高线图来说,比较陡峭的地方,我们的learning rate应该设置的小一点,而相对平缓的地方呢,我们的learning rate应该设置的大一点。所以我们该如何改变这个learning rate?如何随着gradient大小而改变呢?。

我们可以将一个固定的learning rate也就是红框中的
η
\eta
η改成
η
σ
i
t
\cfrac{\eta}{ \sigma^t_i}
σitη
采用RMS,来计算红色框中的learing rate。

Root Mean Square,这一招呢被用在Adagrad中。为什么这个式子会根据gradient的大小而动态变化呢?

右图中的蓝色曲线的gradient比较平缓,算出的gradient比较小,那么对所有的gradient求和取平方之后就比较小,也就是
σ
\sigma
σ比较小,但是由于
σ
\sigma
σ是放在分母的,所以整个learning rate就比较大,那么对于平缓的gradient而言呢,learning rate就比较大。反过来对于绿色比较陡峭的gradient而言呢,learning rate就比较小。
但是呢有时候,对于同一个参数,同一个参数而言,我们的learning rate也需要不同的。


比RMS更好的办法,RMSProp。这里我们需要自己调整
α
\alpha
α的大小。(调参)
我们可以动态调整当前的
g
t
g^t
gt相对于之前的gradient的重要性。
现在一般的optimization的问题呢,我们直接采用Adam来解决。

采用RMS之后呢,会出现红色框框中的,在后面的部分会出现震荡的情况,我们要怎么解决这个问题呢?可以采用learning rate scheduling

也就是对于我们的
η
\eta
η我们也要动态的改变它。其中Warm up在bert中应用的比较多。
最终我们的optimization如下所示:




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








