【IVIF】Equivariant Multi-Modality Image Fusion

2024CVPR Zixiang Zhao团队
分析透彻，方法耳目一新
统一融合架构

1、Motivation

Our approach is rooted in the prior knowledge that natural imaging responses are equivariant to certain transformations

我们的方法根植于自然成像响应对于某些变换的等变性这一先验知识。因此，我们引入了一个新颖的训练范式，包括融合模块、伪感知模块和等变融合模块。这些组件使得网络训练能够遵循自然感知成像过程的原则，同时满足等变成像先验。

对IVIF任务的描述：产生的融合图像减轻了受光照变化影响的可见光图像和易受低分辨率和噪声影响的红外图像的局限性

作者的分析与假设：
我们假设潜在的GT融合图像具有丰富的信息，但在实践中，我们只能通过不同的感知过程来测量相同的GT，这些过程通常是非线性的且难以建模，因此获得了不同模态的观察结果。因此，多模态图像融合问题可以被视为一个具有挑战性的非线性盲反问题，可以被视为以下负对数似然最小化问题：

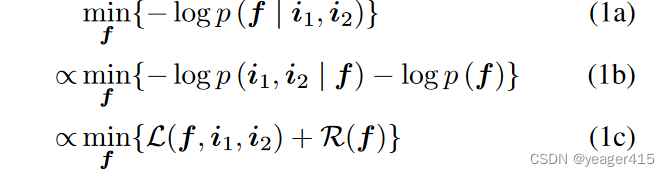
where i1, i2, and f represent two input source images and the output fusion image, respectively. Eq. (1b) originates from Bayes’ theorem. In Eq. (1c), the first term is the data fidelity term, indicating that i1 and i2 are sensed from f ; the second