3.浅层神经网络

3.1神经网络概览

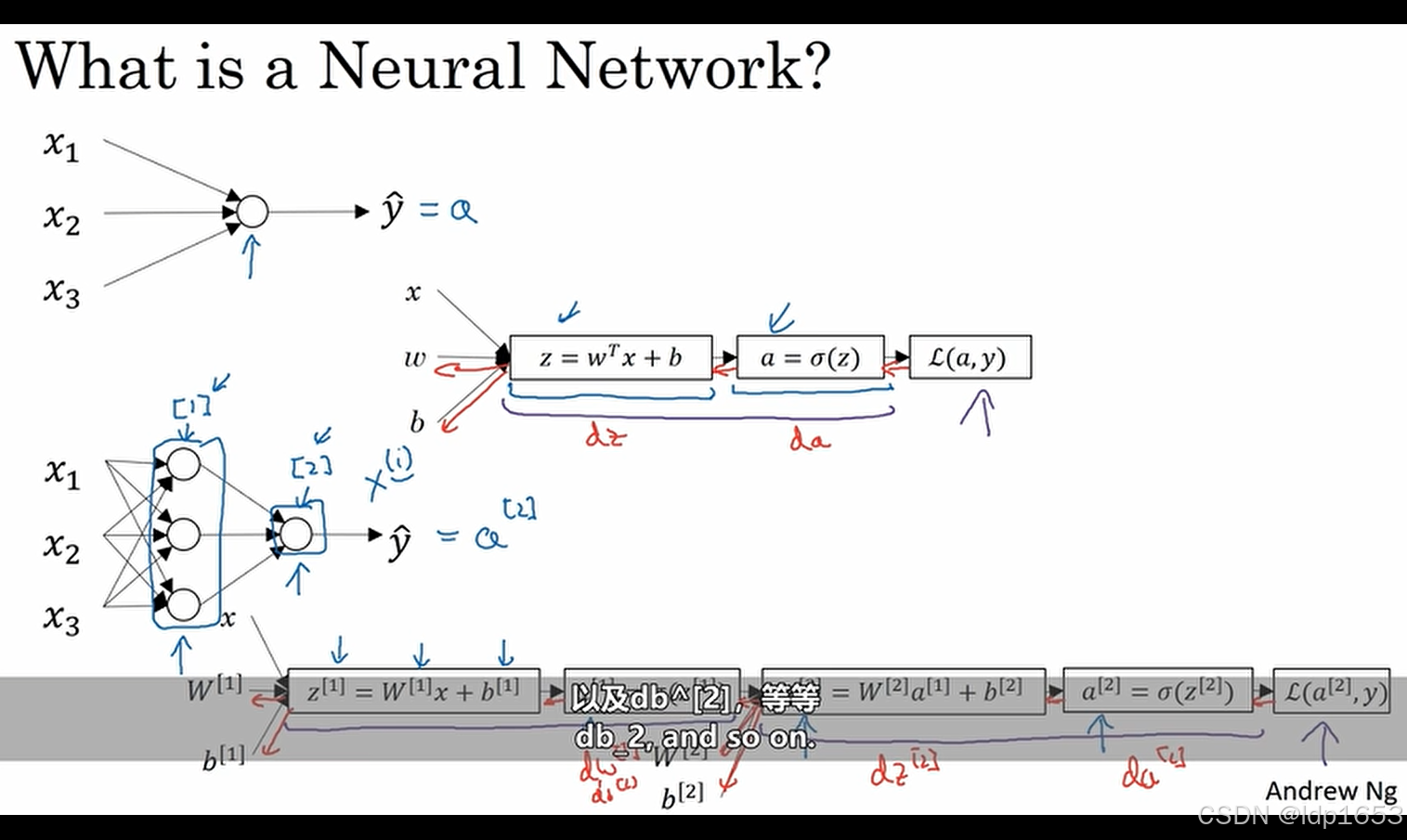
第一个神经元计算z=wtx+b 然后计算a=sigma(z)  

两层的神经网络里 x1 x2 x3表示三个输入特性 第一层[1]算出一个z[1]和sigma[1]

第二层[2]算出z[2]和sigma[2]

先要有一个sense神经网络就是一层一层的计算z=wt+b和a=sigma(z) 最终用最后一层算出来损耗函数L(a,y)

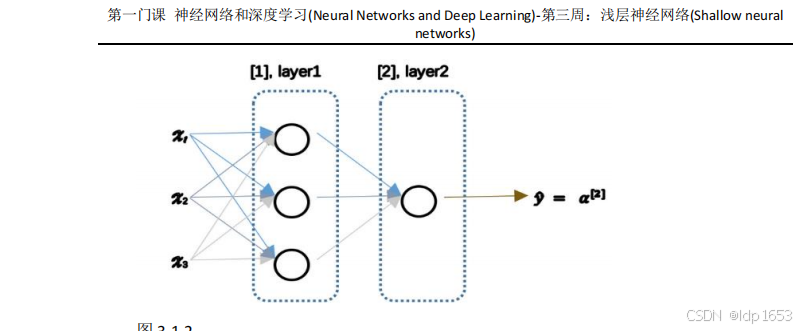
3.2 神经网络的表现形式

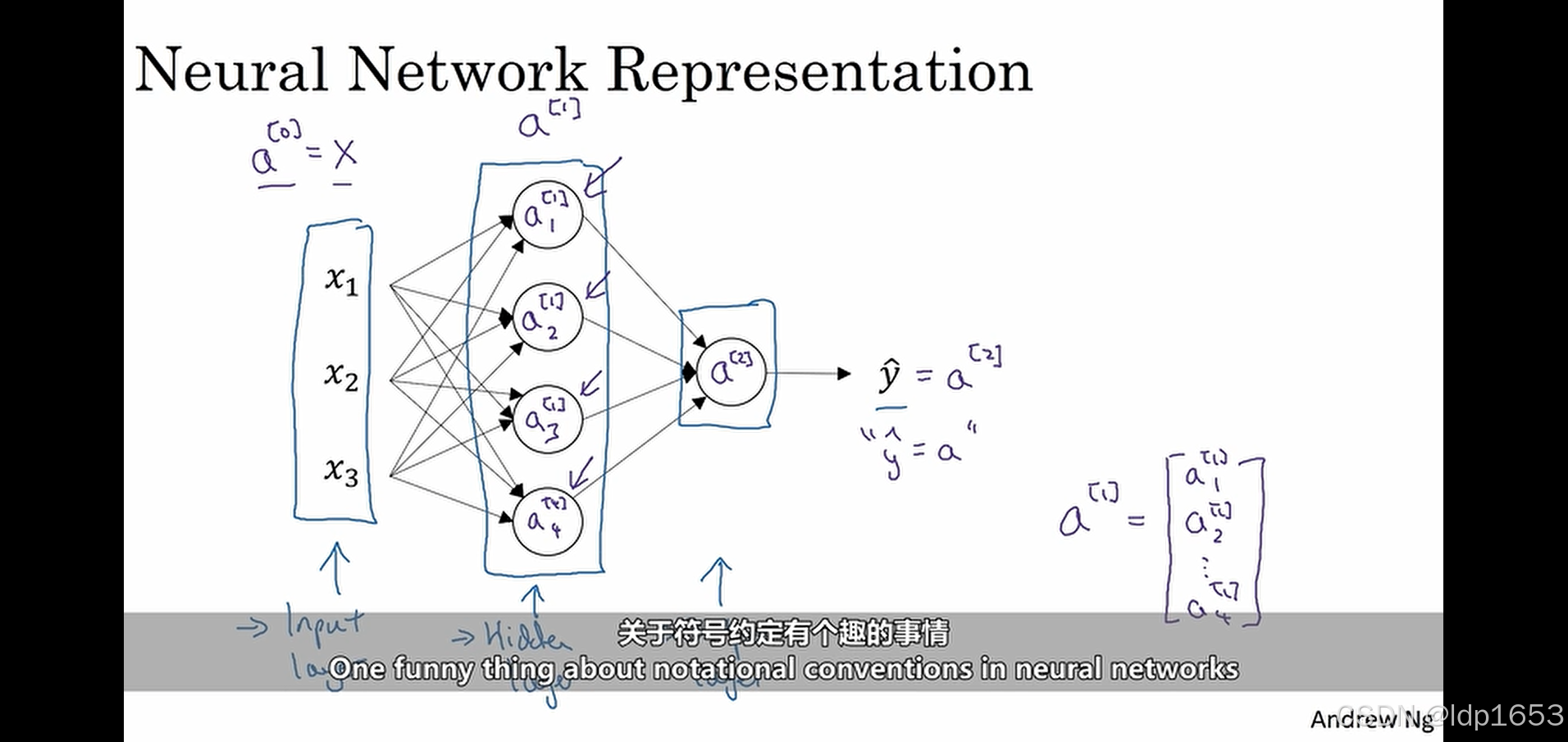
x1x2x3 输入层 中间的层级叫隐藏层  最靠近y帽的是输出层

每层元素的表示方式a[0] 输入层

 a[1]1 a[1]2 a[1]3 a[1]4-组成4行一列的数据 

a[2]

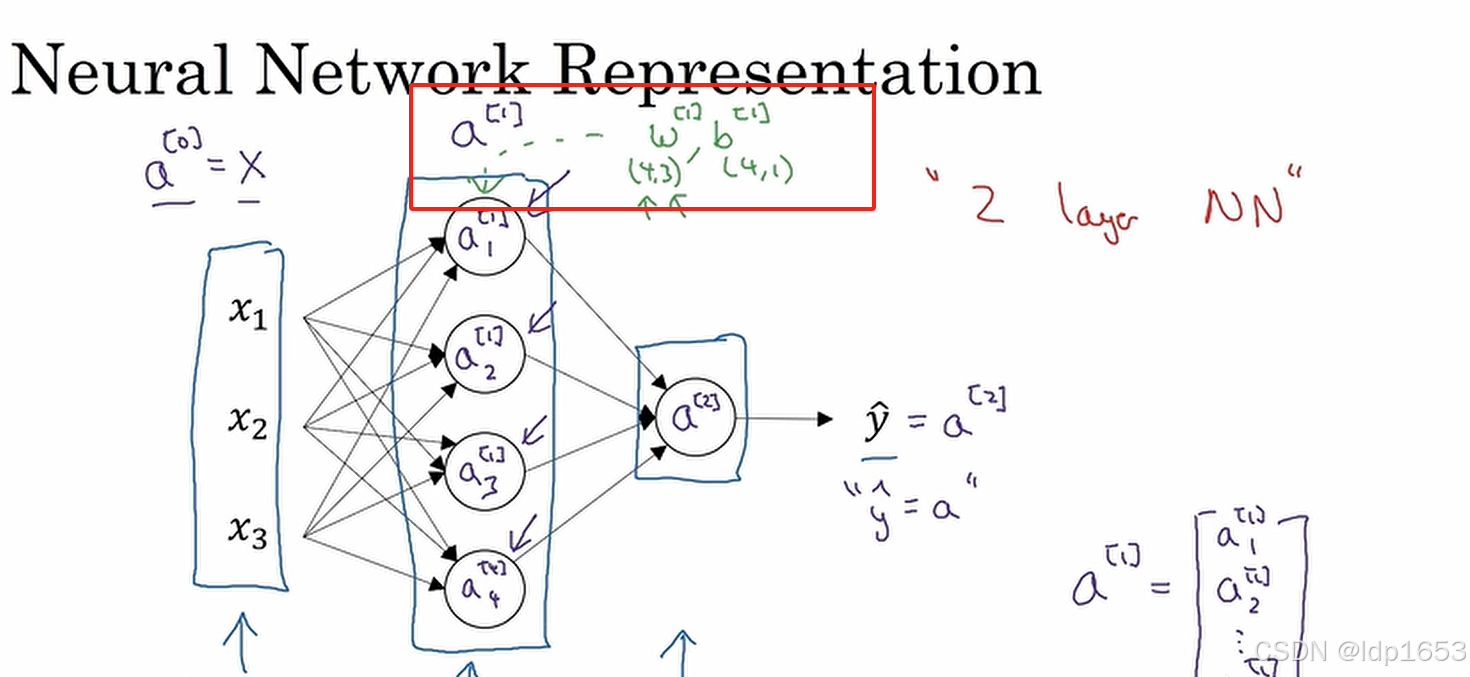
例子里面 x(3,1)的矩阵 W(4，3)的矩阵 b

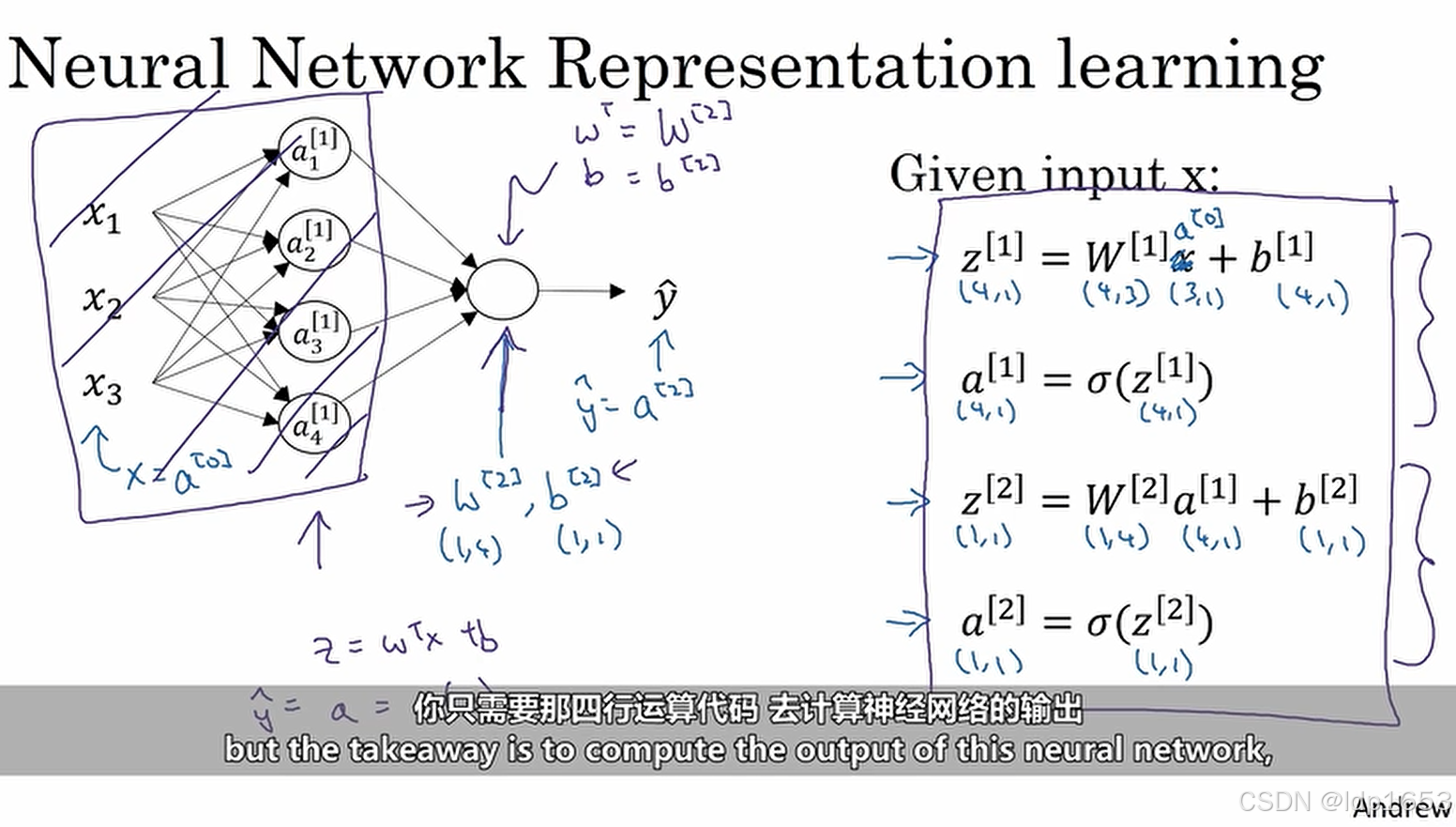
3.3 计算神经网络的输出

一个圆代表两步计算。

1.先算z 2.再算a

隐藏层神经元的计算逻辑。

注意上标和下标。a[1]1 a[1]2 [1]代表层级  1，2，3，4代表 节点编号

更清晰的图，这是一个单一样本

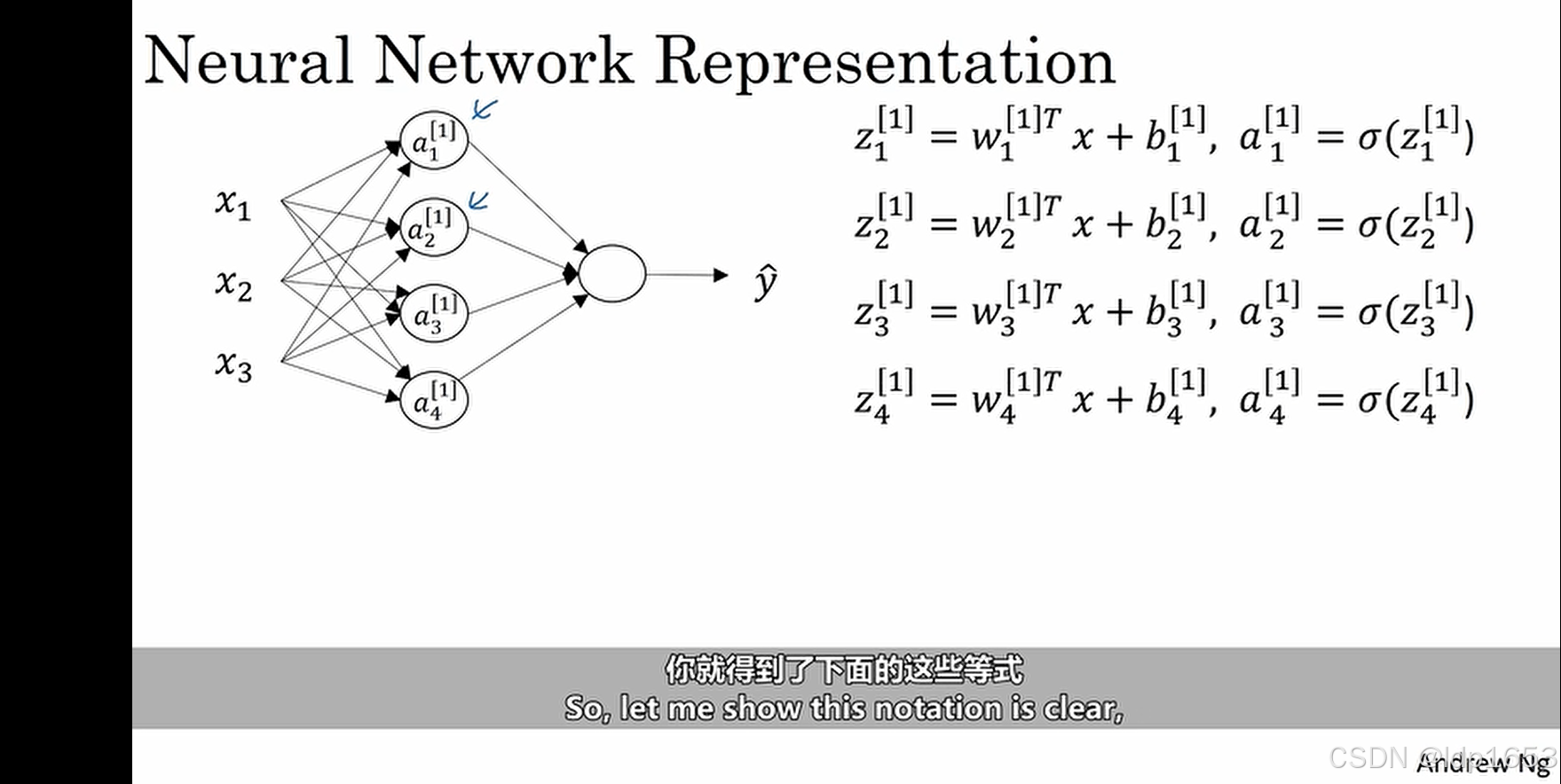
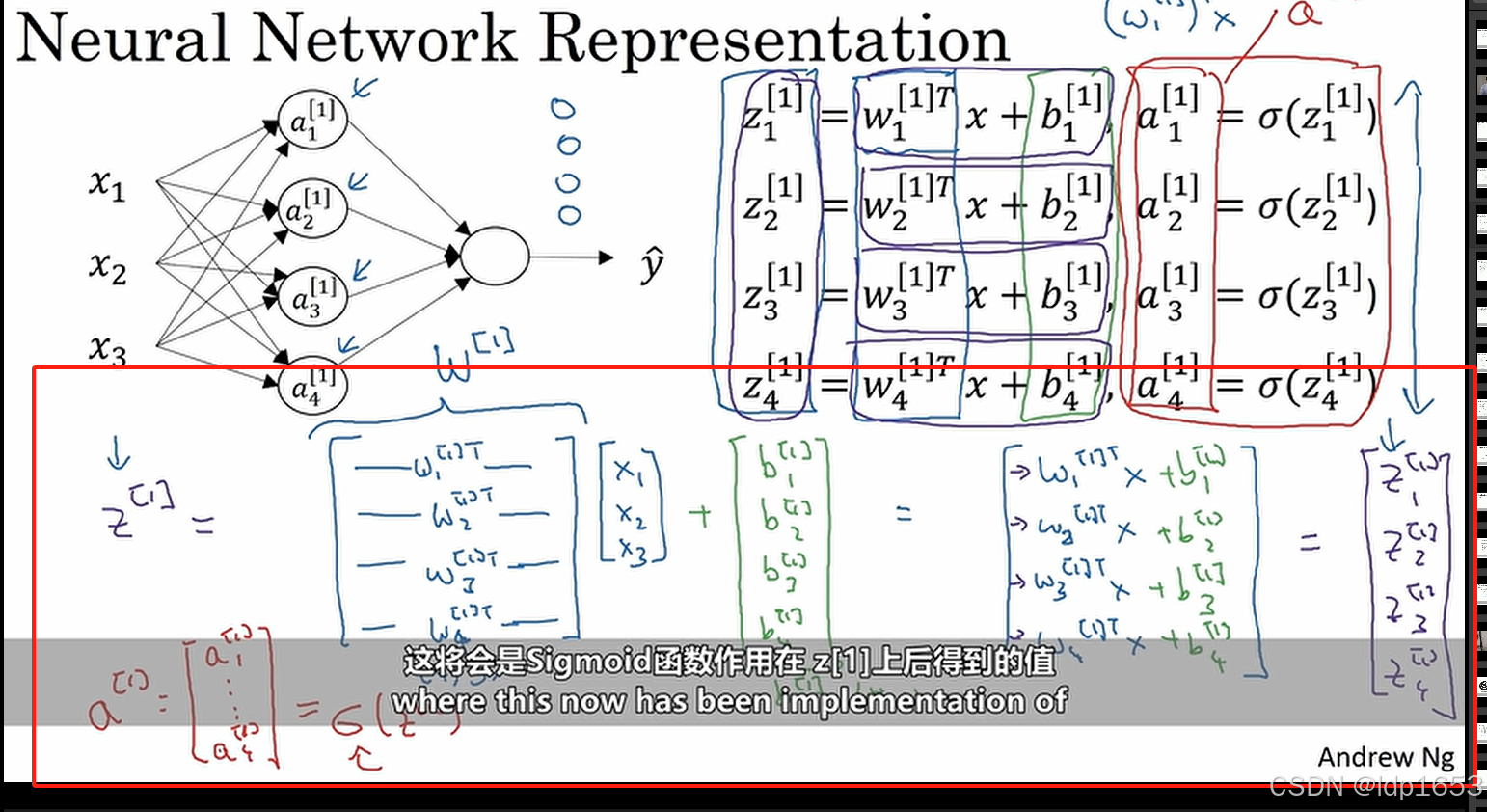
接下来我们要把上图中的四个等式向量化。

在回顾一下矩阵乘法

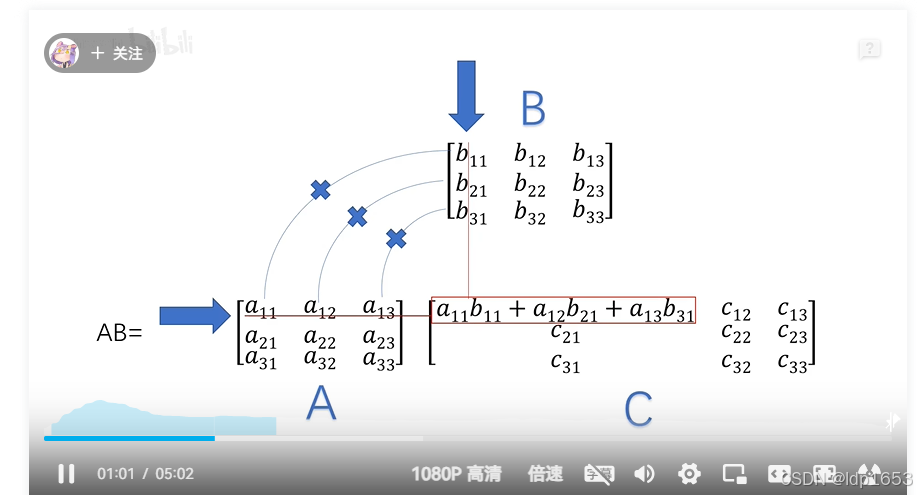
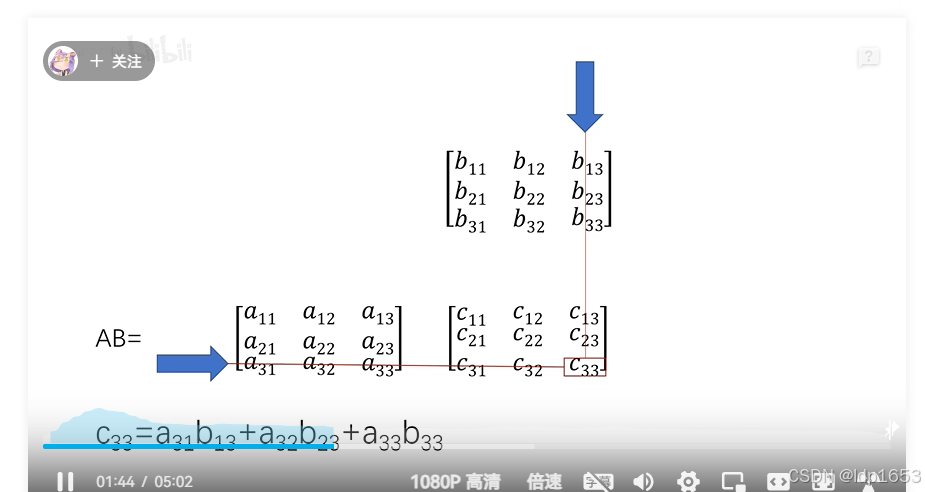
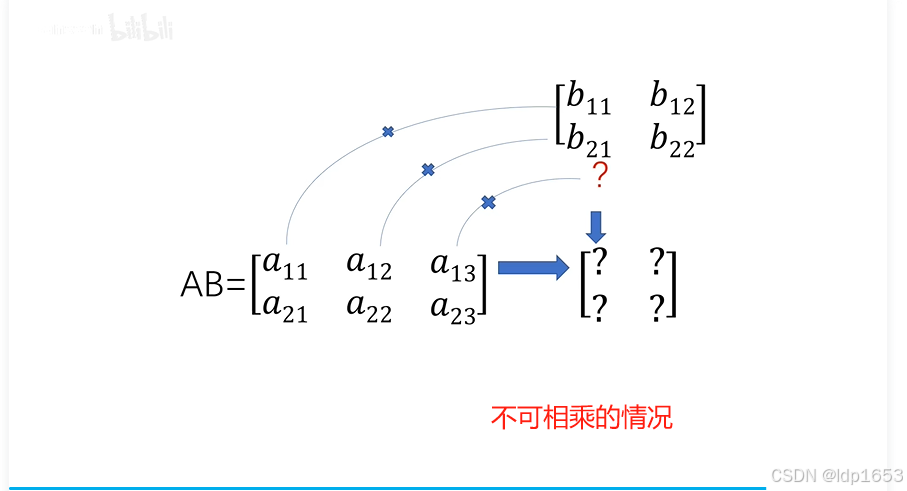
把z11 z12 z13 z14这四个公式以向量的形式计算。

W矩阵(4,3) X矩阵(1,3) b矩阵(4,1)

W矩阵第一行W[1]1,W[1]2,W[1]3,W[1]4 代表四个权重。

先算Z矩阵 Z矩阵算完 用Z矩阵*singma 得到a矩阵

X矩阵别名a[0] y帽矩阵别名a[2]

9行1列的矩阵 叫9维矩阵

9行8列的矩阵 就9*8维矩阵

3.4 多样本向量化

概念: [2]代表第二层 (i)代表第i个训练实例

明确两种写法。代表列向量x(1) x(2) x(3)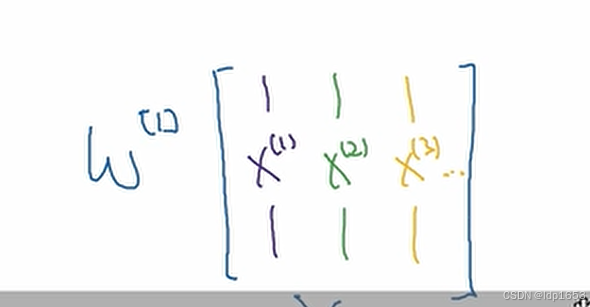

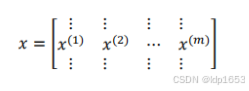
代表矩阵 也就是把实例x1 x2 x3 水平堆叠(按行堆叠)

按行堆叠是指将多个向量堆叠成一个矩阵，每个向量成为矩阵的一行

按列堆叠是指将多个向量堆叠成一个矩阵，每个向量成为矩阵的一列

矩阵A:

矩阵横着来看，每一行从左到右表示所有的训练实例。

第1行第2个 第3个表示 神经网络第1个隐藏单元对于第2个，第3个训练实例的激活值

竖着来看对应神经网络不同节点。是对应隐藏单元号码。

第1行第1个表示 神经网络第1个训练实例的第1个隐藏单元的激活值。

第2行第1个表示 神经网络第1个训练实例对第2个隐藏单元的激活值。

矩阵X:

横向看就是不同的训练实例 

竖着看是不同的输入特征(也就是输入层的不同节点)

3.5 向量化的解释

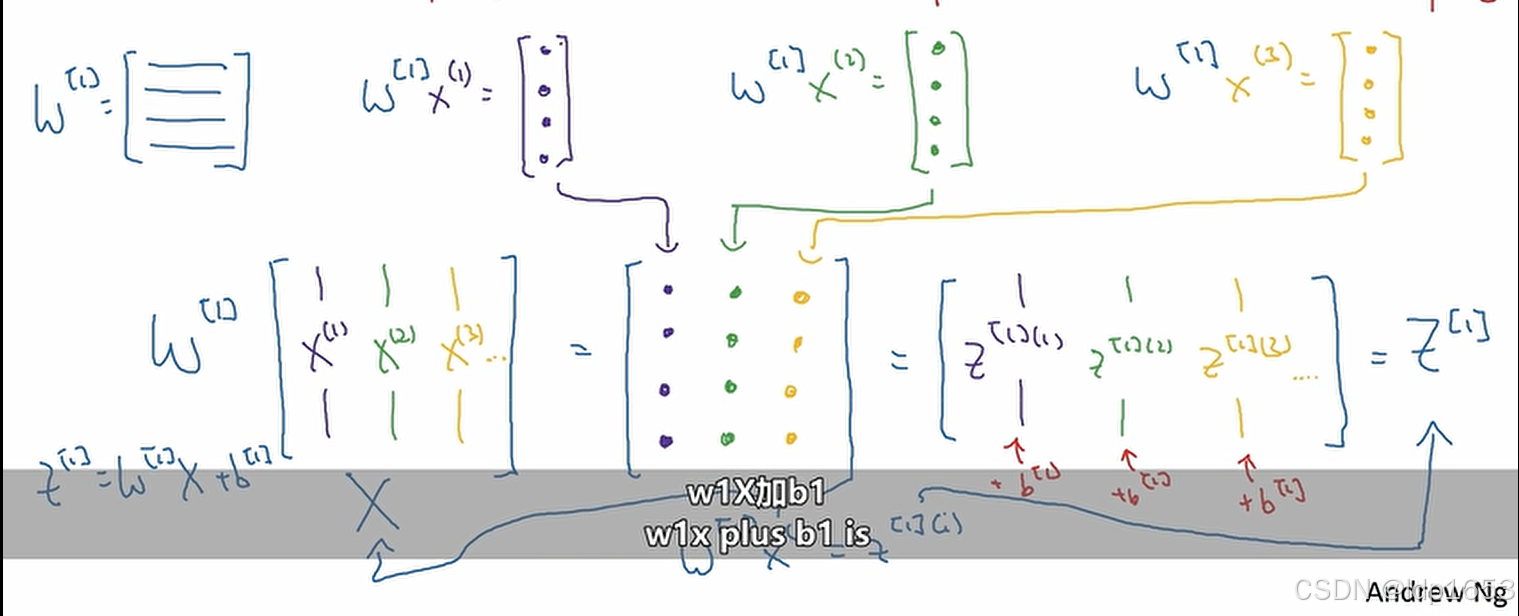
根据右上的四条公式可以看出，神经网络的每一层都在进行重复逻辑(先算z再算a)的计算。

需要注意的是，截止到目前一直用sigma函数作为激活函数，但是他不是最好的选择，下一节会介绍更多的激活函数。

3.6 激活函数

tanh(z):

tanh(z)作为激活函数 ,他拥有一种数据居中的效果，就优于sigmad,所以教授基本不会选择sigmad作为激活函数。 

但是只有一种情况会选择sigmad作为激活函数，那就是二元分类(输出是0或者1)的时候，因为当y的取值范围是0-1时，y^的值域也是0-1

tanh和sigmad共同缺点就是当z特别大或者特别小的时候，函数的导数（斜率）就会无限趋近于0，会减慢梯度下降的速度。

Relu函数:

z大于0的时候导数为1 z小于0的时候导数为0

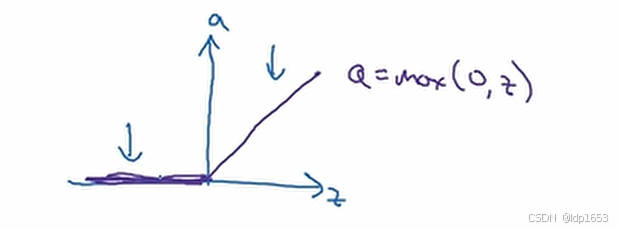
大致选择激活函数的规则:

输出为1或者0(二分类)的场景：sigmad

其他场景不知道选啥的时候：选Relu 由于有比较少的因素可以影响函数斜率趋近于0(大多数样本可以让z大于0)，所以他的计算速度比sigmad和tanh快。

复习一下三个函数:

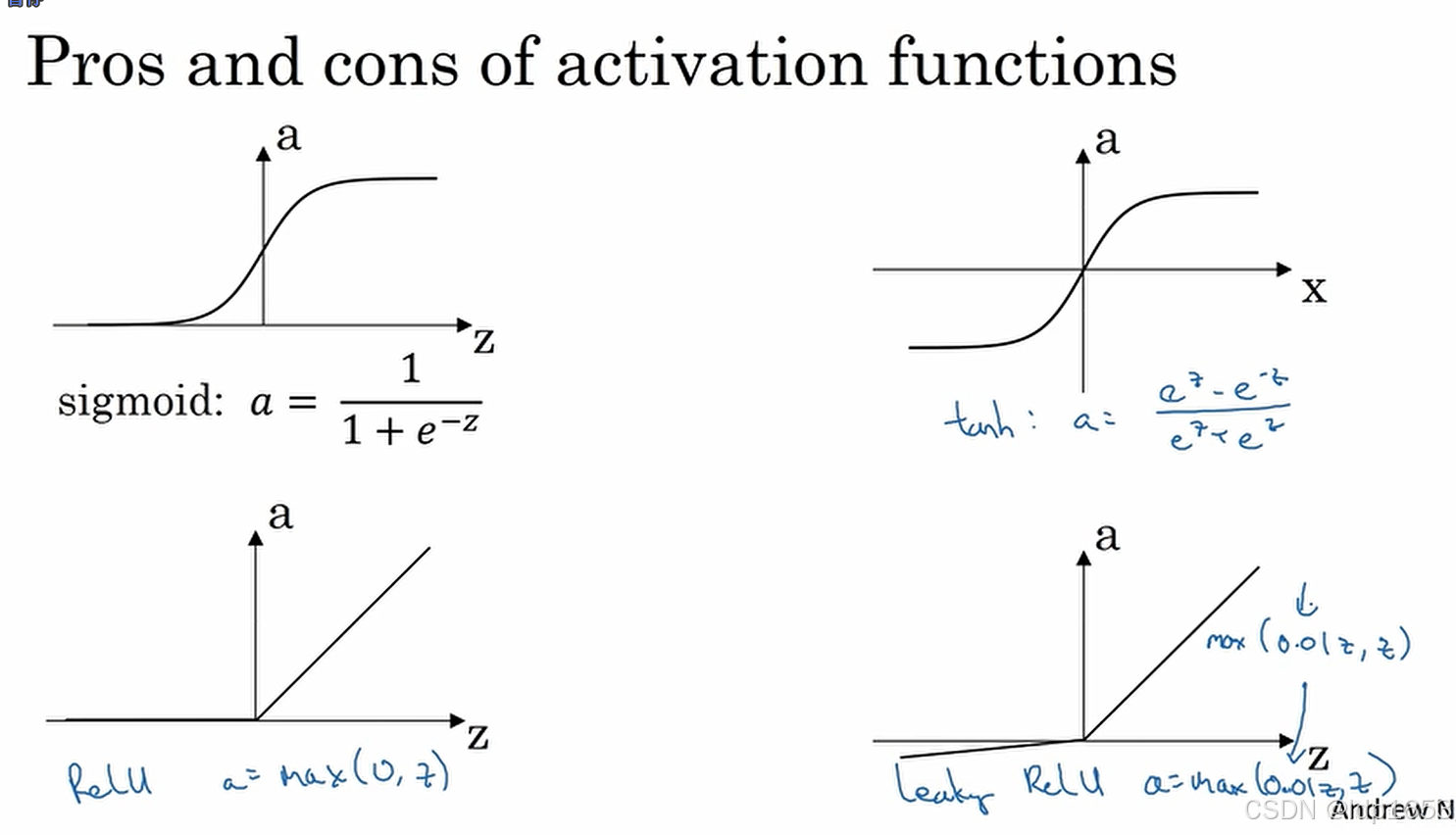
3.7 为什么需要非线性激活函数

如果使用线性激活函数、那么神经网络的输出就仅仅是输入函数的线性变化。(无论神经网络多少层)

3.8 激活函数的导数

概念:下图的写法表示 

g′(z) 表示函数 g(z) 对变量 z 的导数，其定义为 g(z) 随 z 变化的速率，数学上表示为：

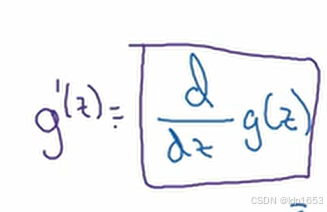
3.9 神经网络的梯度下降公式以及推导

3.11 权重随机初始化

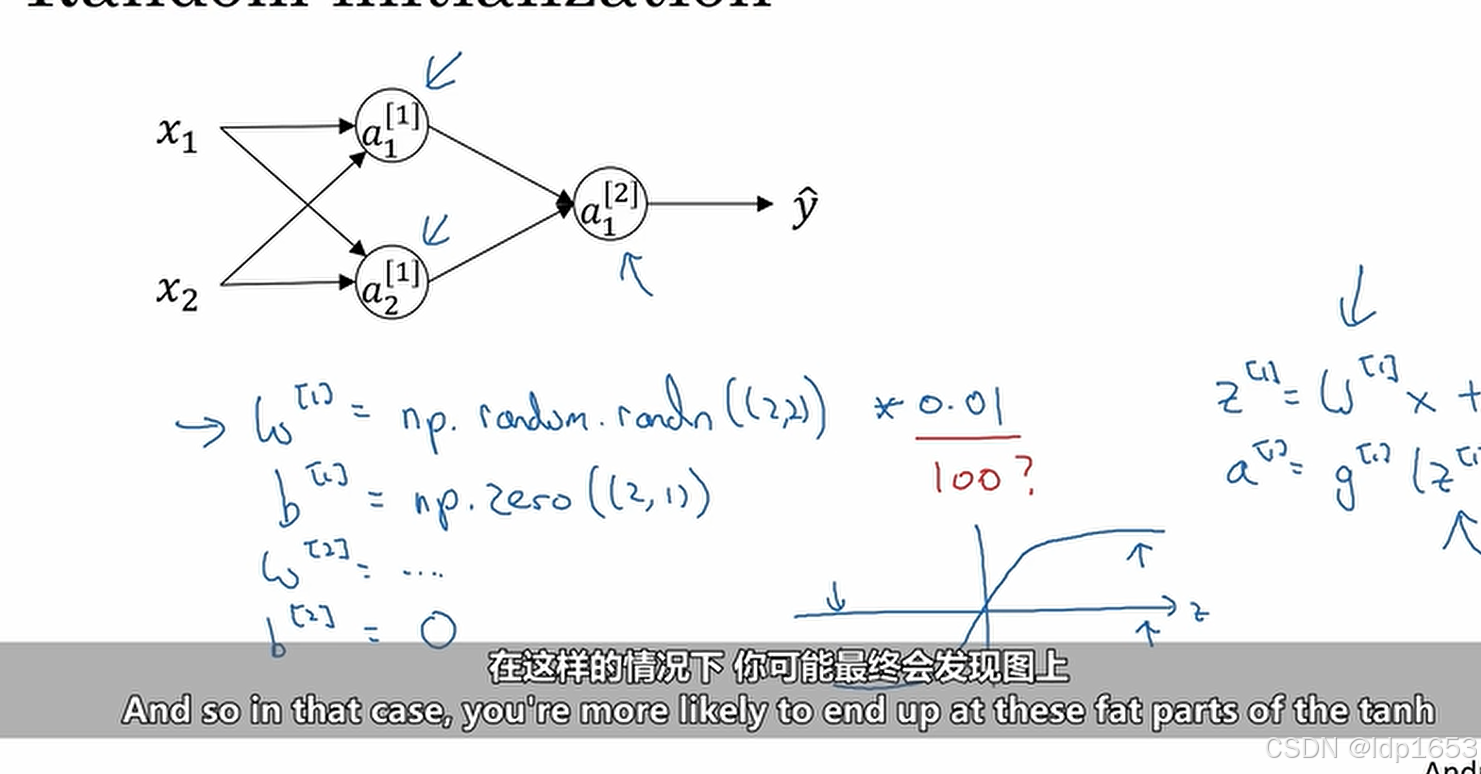
如果初始化权重参数矩阵W里所有元素都为0，那么所有隐藏单元都负责相同的计算功能，但我们希望不同的隐藏单元负责实现不同的计算功能，重复的计算没意义！

b矩阵不会因为初始值为0而引发对称问题。所以b矩阵可以初始化为0.

而且W初始值要尽可能的小,如果W过大(比如像下图里*100)，Z的绝对值会很大，这样tanh和sigmad的斜率就会特别小，导致学习进度特别缓慢。这就是公式里要*0.01的原因。

0.01的适用范围:浅层的神经网络

深层的神经网络参数选取：下一节讲