2.神经网络的编程基础

2.1 二分类

在二分类问题中，我们的目标就是习得一个分类器，它

以图片的特征向量作为输入，然后预测输出结果𝑦为 1 还是 0，也就是预测图片中是否有猫

64*64像素的图像的存储

在计算机里对应3个 64*64的矩阵

像素总量=64*64*3=12288 们用𝑛𝑥 = 12,288，来表示输入特征向量的维度

符号

x，y，X，Y，Mtrain Mtest，矩阵X，矩阵Y X.shape Y.shape

输入矩阵X 高度为nx 长度位m，输出矩阵Y 高度为1 长度位m

2.2逻辑回归

用逻辑回归解决二分类问题。

想要得到y=0或者y=1 需要用到一个输入为x的线性函数。y=wTx +b 

但是要控制他的值域在(0，1)

所以用到的就是sigmoid 函数。

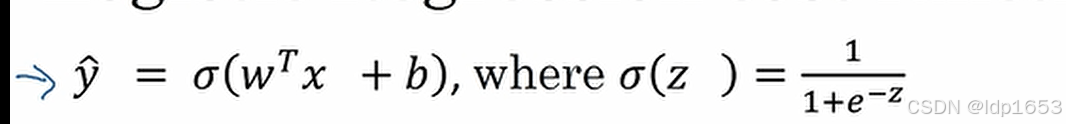
z=wTx+b

z越大e-z次方越小，无限趋近于0，分母无限趋近于1，sigmoid 函数值无限趋近于1

z越小e-z次方越大，分母无限趋近于0，sigmoid 函数值无限趋近于0 所以得到下图函数走势。

2.3逻辑回归代价函数

损失函数(代价函数):

定义在单个训练样本里 又叫误差函数。我们通过这个𝐿称为的损失函数，来衡量预测输出值和实际值有多接近。

𝑦^ 是逻辑回归函数的预测值。y是样本输入的真实值。

𝑦^ 就是逻辑回归函数sigmoid 取值范围0-1 开区间

Loss function:𝐿(𝑦^ , 𝑦). 我们想让损失函数的值无限趋近于0

逻辑回归中用到的损失函数是：𝐿(𝑦^ , 𝑦) = −𝑦log(𝑦^) − (1 − 𝑦)log(1 − 𝑦^)

列举y=1和y=0的情况会发现。

y=1时 需要尽可能让𝑦^ 变大=1.

y=0时 需要尽量让𝑦^ 变小=0

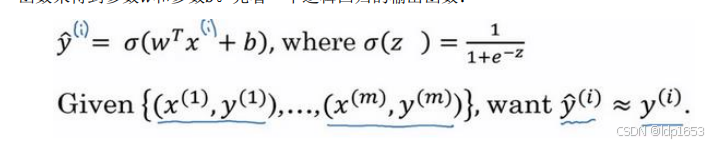
算法的代价函数(损失函数):

全部训练样本损失函数的平均值：

所以在训练逻 辑回归模型时候，我们需要找到合适的𝑤和𝑏，来让代价函数 𝐽 的总代价降到最低

2.4梯度下降法

现在都目标就是找到𝐽(𝑤, 𝑏)函数值是最小值，对应的参数𝑤和𝑏。

梯度下降法说白了就是找到函数最低点，通过一点点求导的方式，逐渐从初始点(w1,b1)往w,b两个方向来求偏导，最终把初始点引导最低点(w2,b2)

偏导数和全导数

对x求偏导，可以把y z看成常量。

对x求全导，yz还需要对x求导。

导数通俗来讲就是斜率

2.7 计算图

个人理解就是按照计算的先后顺序做变量的替换，然后按照步骤计算求结果。也就是按照图中的蓝色方向从左到右来计算。

2.8 计算图求导数

上图红色剪头就属于反向来求导，是为了推断某个变量的变化对输出变量的影响。

在反向传播算法中的术语，我们看到，如果你想计算最后输出变量的导数，使用你最关

心的变量对𝑣的导数，那么我们就做完了一步反向传播，在这个流程图中是一个反向步。

术语dvar:输出变量对某个变量的导数。

对于最终变量J来说 dv=3,da=3

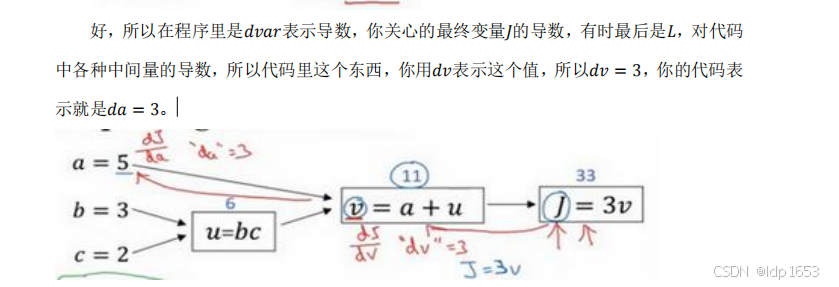
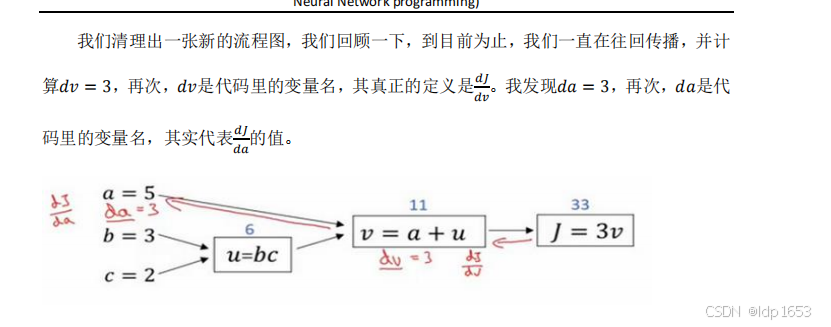
2.9 逻辑回归中的梯度下降

单个样本的梯度下降。

w1，w2可以理解为两个权重

L为损耗函数. y是每次模型输入的准确值，a为逻辑递归函数算出的y^(模型预估值)

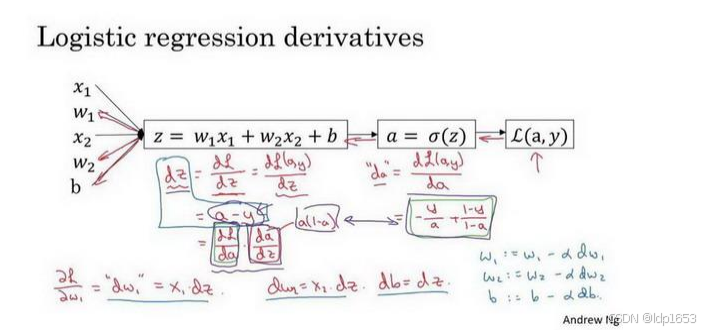
1.L对a求导 用da表示  

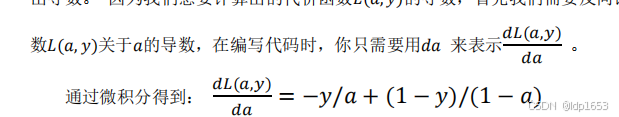
2.L对z求导用dz表示

3.最后一步  也是我们的最终目标 分析 w和b对L的影响 

得出

4.套进逻辑回归成本函数

使用公式𝑑𝑧 = (𝑎 − 𝑦)计算𝑑𝑧，

使用𝑑𝑤1 = 𝑥1 ⋅ 𝑑𝑧 计算𝑑𝑤1， 𝑑𝑤2 = 𝑥2 ⋅ 𝑑𝑧计算𝑑𝑤2， 𝑑𝑏 = 𝑑𝑧 来计算𝑑𝑏，

由下面逻辑回归的代价函数可知

w=w-a.dw

b=b-a.db

得到𝑤1 = 𝑤1 − 𝑎𝑑𝑤1， 𝑤2 = 𝑤2 − 𝑎𝑑𝑤2， 𝑏 = 𝑏 − 𝛼𝑑𝑏。

逻辑回归的成本函数概念复习:

a是逻辑回归的输出。

2.10 m个样本的梯度下降

损失函数定义要时刻牢记:

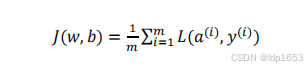
ai是每次训练样本的预测值，yi是每次样本的准确值(监督值)

2.11向量化

向量化会大幅度提高运算速率，避免了for循环的使用。

w和x都可以是n维的列向量，每一个维度都可以代表一个特征。如果不采用向量的方法，那么就要在循环里进行x次的 w*i的计算。

向量方式只需要一行: z=np.dot(w,x)+b

每次想要使用低效的循环时，要先去看看使用numpy的内置函数！！用向量化的思维解决问题。

2.13 向量化逻辑回归

有m个训练样本。

Z=w^TX+b ，都是(nx,m)  w代表的是权重。W矩阵是(1，nx)

最后想一次计算得到z矩阵(1,m) 一行m列。[z1,z2,z3...,zm]

求完z矩阵之后想求a 得到A=[a1,a2,a3...am]

numpy 命令是𝑍 = 𝑛𝑝. 𝑑𝑜𝑡(𝑤. 𝑇, 𝑋) + 𝑏。

𝐴 = [𝑎 (1)𝑎 (2) . . . 𝑎 (𝑚) ] = 𝜎(𝑍) ，之后再通过恰当地运用𝜎一次性计算所有 𝑎。

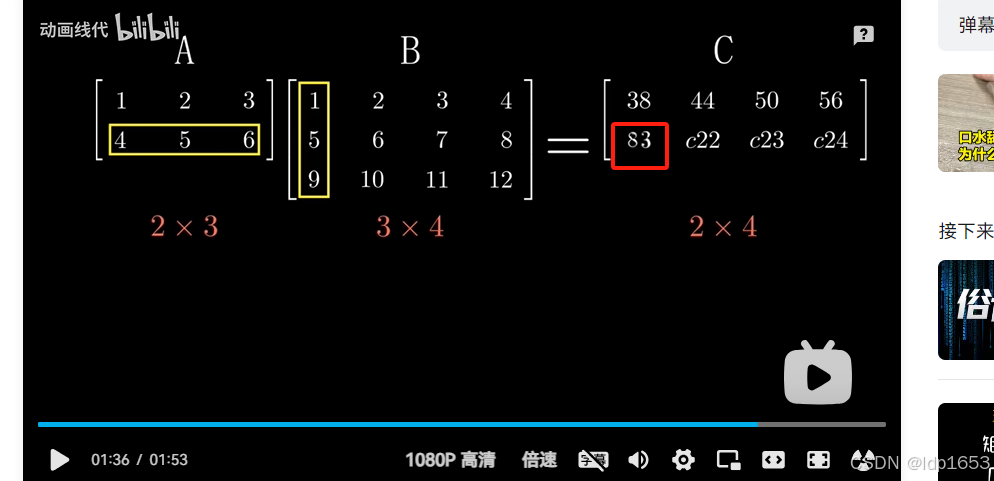
矩阵的转置

矩阵乘法

内项不一致没法进行矩阵乘法

内项一致才可以矩阵乘法 

内项一致，外项组成结果矩阵 --2x4结果矩阵

目标矩阵 

2.14向量逻辑回归的梯度输出

前五个公式完成前向传播和后向传播。后两个公式完成了一次梯度下降。需要进行多次梯度下降，还是需要使用for循环。

2.15 python中的广播

axis 用来指明将要进行的运算

是沿着哪个轴执行，在 numpy 中，0 轴是垂直的，也就是列，而 1 轴是水平的，也就是行。

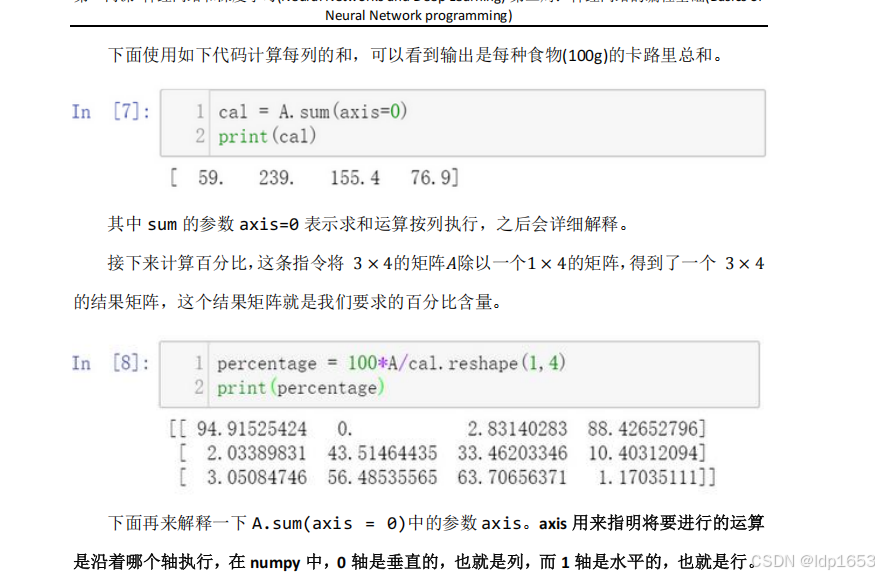
广播:会把常量自动变成矩阵。

2.16 关于 python _ numpy 向量的说明

每次创建数组的时候得让他成为向量。(5,1)列向量，5行一列。  (1,5)行向量，1行5列

(5,1) 5行1列 列向量:

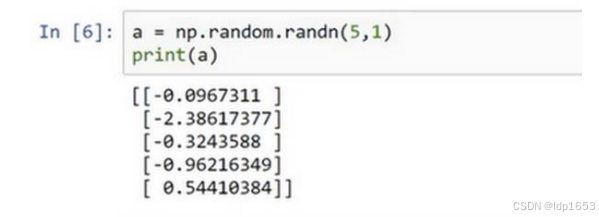
使用断言，来吧向量类型固定。