FIR滤波器Matlab

FIR滤波器的Matlab实现

一、Matlab实现hamming，hanning时域窗函数相乘法。

FIR与IIR滤波器相比，除了计算量大些，其他都优于IIR滤波器，比如具有线性相移，设计过程简单。而对于计算机的，计算量大已经不算缺点。所以FIR是比IIR更加优秀性能的滤波器。
线性相移有什么好处呢，就是不同频率具有固定的时间延迟，整个滤波器后的波形具有严格的相似性。

1、简要的matlab设计代码

给出正确的滤波器输入参数，首先要知道，数字滤波器都是2π归一化的，2π对应fs采样率。这一点和FFT结果是一样。采样时间离散序列，频谱以2π为周期，（也是以Fs为周期）。比如通带200Hz，阻止500Hz，采样率Fs=100000Hz。
% %------------------------------低通滤波器2----------------------------------

%filter()实现，原始数据data进行滤波，即data与firfilter_numt的卷积。
%======================================================
如果除了对matlab的简单使用，还想有一点点个人层面的理解，可以如下看

二、FIR滤波器的理解

因为理想滤波器具有很好频率特性，但是因为其时间响应长度无限。所以在时间域序列中，我们要用一个窗函数来把它截断，我们需要一种理想方式的截断。
比如hamming窗截断，在频域看来具有通带、阻带波动小的特点。fir1函数实现了理想低通滤波器的时域无限长序列h(t)与汉明窗window相乘，生成一个有限长的序列。即对h(t)的加窗截断。
为啥要加窗截断，而不是直接截断。数字域直接截断称为矩形窗截断，我们是从频域来看哪种滤波器性能好，时域直接矩形窗截断，频域起伏较大，约9%（-20dB）的波动，而且不随矩形窗加宽而减小，波动峰只是随宽度加大，向过渡的边界靠拢而已，也就是吉布斯现象，这样的频域特性肯定不好啦。我们希望波动小一些，而且可以承受频域过渡区域加宽一些的牺牲，因此有了各种窗，比如升余弦窗（hanning,hamming,blackman）。

如果你想进一步深究FIR滤波器的理论基础可以继续向下看

三、FIR滤波器的理论基础

**1、线性相移条件
假设有限项系数，b(k)能够实现线性相移滤波，则可以推断b(k)特点：

2、幅度特性**

当n为偶数时，将h(n)代入傅里叶变换，会得到频率为π是H(w)=0。但是n为奇数时不会（这个过程需要计算）。被告知总结如下。

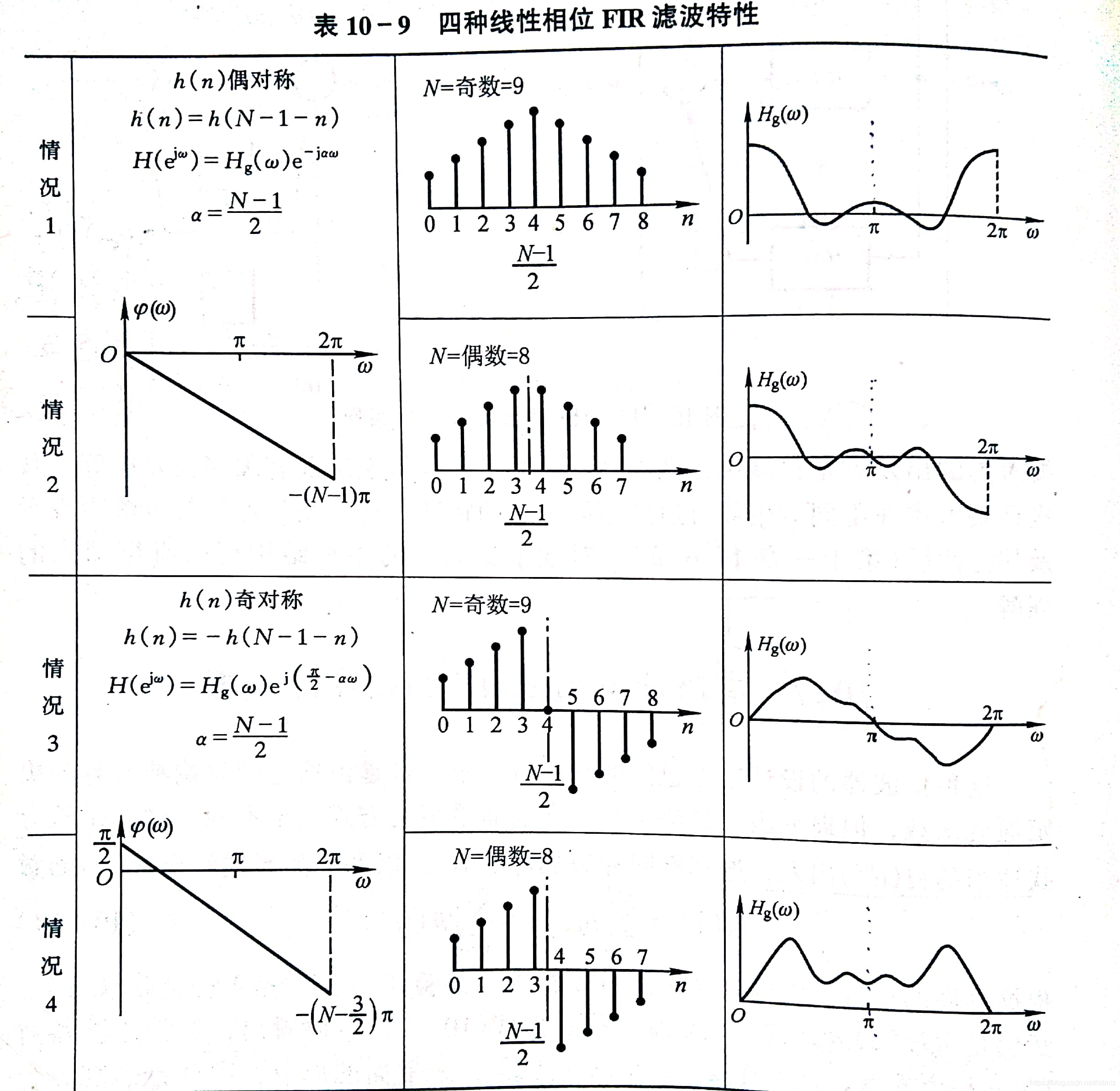
π代表最高频率(采样率一半，Fs/2)，0代表最低频率。可见n为奇数时，0和π都不为零，也就是没有低频和高频限制，因此最方便的设计特性。通常我们就去h(n)偶对称，n为奇数这种设计方法。