优化算法精要-优快云博客

本文链接：https://blog.youkuaiyun.com/l898985121/article/details/114292673

泰勒展开

参考文献：
【1】https://www.zhihu.com/question/25627482

泰勒展开：用多项式函数，在某一个点附近，逼近原函数。
原因：因为多项式函数求导等运算比较方便，有良好的性质
下图是一个例子，不断用多项式去逼近 $e^x,x=2$ .
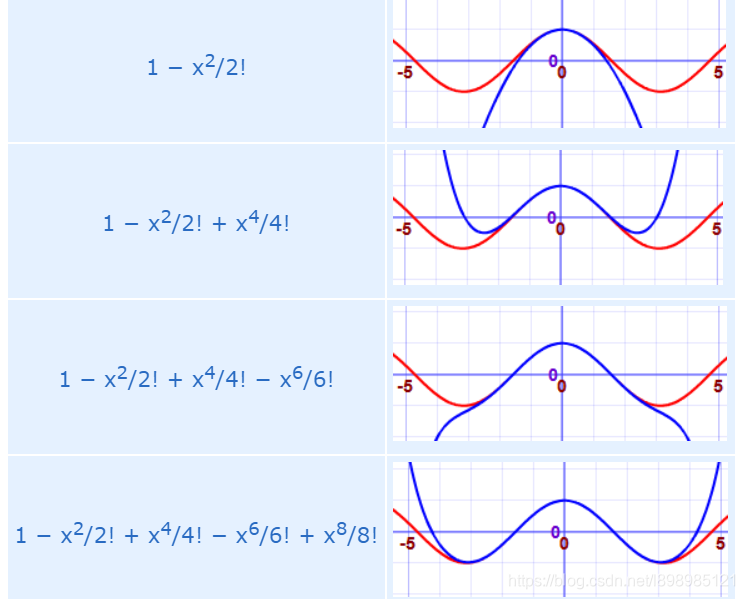
在这里插入图片描述

所以最初的想法可能就是仿造一条简单一点的曲线，让在一个点处的各种导数都相同就行
在这里插入图片描述
先是普通的相等

然后逐渐复杂

最复杂

最后得到式子：

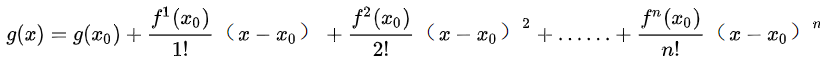
雅阁比矩阵

一个N到M维的映射：
在这里插入图片描述
有矩阵：

海塞矩阵

感觉中文的wiki比英文的wiki写的还好一些
参考资料：
【1】https://zh.wikipedia.org/wiki/%E9%BB%91%E5%A1%9E%E7%9F%A9%E9%99%A3
对于一个N到1维的映射：
在这里插入图片描述
有矩阵：

和泰勒展开雅各比矩阵关系

一元函数泰勒展开：
在这里插入图片描述
二元函数泰勒展开

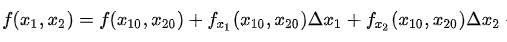
其中：

写成矩阵形式：

$G(x_0)$ 为在 $x_0$ 点的海塞矩阵：

由于：

所以海塞矩阵为对称阵

推广到多元函数有：
在这里插入图片描述
其中：

可以看到，一个函数在点 $x_0$ 处的海塞矩阵就是在该点梯度的雅各比矩阵：

应用

经常用在优化当中，将一个目标函数进行泰勒展开：
在这里插入图片描述

牛顿法（newton’s method）

求根

如下图是迭代求根过程
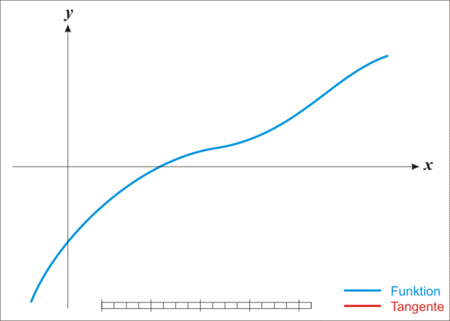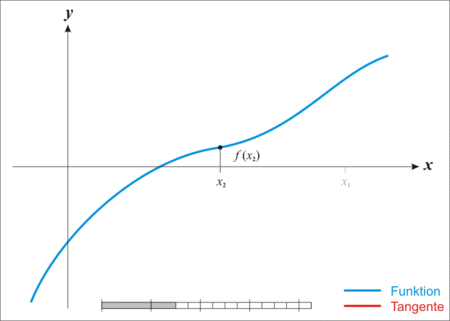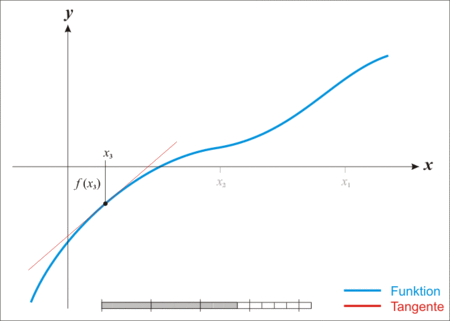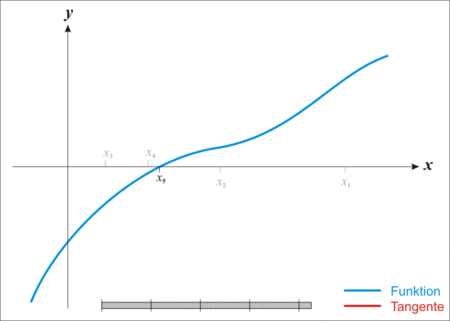
在这里插入图片描述
首先取曲线上一个点，构造一条切线：

令切线的y=0：

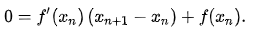
求出x：

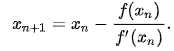
求极值

求如下极值：
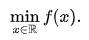
在这里插入图片描述
泰勒展开：

导数等于0：

得到：

更新：

求极值的高维情况：

对于一个多元函数f，f是一个标量，有：
在这里插入图片描述
如下图：左图可以想象成：
$f(x,y)=x^2+y^2$
右图

高维迭代过程可以类比一元函数的情况：

拟牛顿法

从上面的牛顿法更新权重的方式看，需要求海塞矩阵的逆，这个计算比较耗时，有时候可能也有问题，因此，需要替换掉海塞矩阵，用一个矩阵去近似。

高斯牛顿法

参考资料：
【1】https://math.stackexchange.com/questions/1105214/difference-between-newtons-method-and-gauss-newton-method
【2】https://blog.youkuaiyun.com/jinshengtao/article/details/51615162
在求解最小二乘形式的问题中，可以用一种更简洁的方法来替换海塞矩阵。

比如要计算如下目标函数的最小值：
在这里插入图片描述
其中 $e (x)$ 是误差函数， $e(x)\in R^m,x\in R^n$ ，
按照之前的，将f(x)泰勒展开，保留到2次项，然后求导可得：

令导数等于零：

这个就是牛顿法的更新，需要求H的逆。
由于上面提到的，海塞矩阵是梯度的雅各比矩阵，因此有：
在这里插入图片描述
其中：

忽略 $H e (x)$ 那一项，可得：

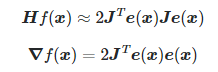
进而得到高斯牛顿法的更新方式：

下面这个资料里的描述也是类似的