CDA 数据分析师 Level1-基本知识4

一.基础知识

统计学是数据分析中的核心要素，也是CDA考试中的重点难点，因此将在这篇文章中对统计学以及CDA考试中的计算题进行总结和帮助读者能更好的理解掌握

数据分析有2类：
一类是描述性分析，
一类是推断性分析，
描述性分析包括总体规模，对比关系，集中趋势，离散程度，偏态，峰态等等，
推断性分析包括估计，假设检验，列联分析，方差分析，相关分析，回归分析等等

数据类型按计量尺度分三类：
分类型数据（不可排序，不可计算，例如：男女），
顺序型数据（可排序不可计算，例如：一等奖，二等奖），
数值型数据（可排序可计算，是最高级别的数据类型）

集中趋势：均值不等式：算数平均数≥几何平均数≥调和平均数

离散趋势：
极差：最大值和最小值的差值，离差，方差，标准差，离散系数（去掉量纲，越大越离散，标准差除均值）

1.当一组数据属于左偏分布时，众数在右边，平均数在左边
2.截面图数据应注意异方差
3.四方位差较少受异常值的影响， 极差，方差，标准差容易受异常值的影响
4.中心极限定理的假设包括样本相互独立，样本具有相同的分布，样本足够大，不包括样本服从正太分布
5.样本为小样本，且具体方差未知适合用t检验统计量
6.SQL对大小写不敏感，SQL为非过程化语言
7.全部变量的方差相同适用于协方差矩阵计算
8.在因子分析中，可以对因子进行旋转，使其意义更明显
9.K均值聚类需要指定聚类个数
10.快速聚类占内存少，计算量小，处理速度快，适合大样本，需要事先确定多少个类别，不能对变量进行聚类
11.逻辑因回归的因变量属于定性变量
12.德尔菲法不能用来分析时间序列数据
13.时间序列中，应除去长期趋势，循环变动和不规则变动
14.RFM 的F 说明客户的兴趣度
15.右偏分布：卡方分布，F分布，对数正太分布
16.若检验统计量F近似等于1，说明组间方差不包含系统因素的影响，方差分析中不应该拒绝原假设
17.主成分分析中确定主成分个数的原则是特征根大于1，累积特征根值加上总特征根的百分之80以上
18.利用统计学定义的距离进行度量的聚类方法是：层次聚类法，快速聚类法
19.两变量独立，皮尔森系数必定为0，若皮尔森系数不为0，两变量必定不独立，两变量不独立，皮尔森系数不一定不等于0

二.计算题

1.算数平均数：（x1+x2+x3…+xn）/n ，加权算数平均数(M1f1+M2f2+…Mnfn)/n，特点：容易受极端值影响

2.几何平均数：n次√(x1*x2…xn)，加权几何平均数(f1+f2+…fn)√(M1)的f1次方+（M2）的f2次方…（Mn）的fn次方）特点：容易受极端值影响，所有数大于0，用与增长率的研究

3.调和平均数：H=n/((1/x1)+(1/x2)+（1/x3…(1/xn))，加权调和平均数：H=n/(f1/M+f2/M+…fn/M)特点：容易受极端值的影响，数据不能为0，用于效率数据的研究

4.极差：最大值max减最小值min，特点：容易受极端值影响，未考虑数据分布

平均差：绝对值((x1-平均数x）+（x2-平均数x）+…（xn-平均数x）)/n，特点：能全面反应数据离散程度，求出来的值越大越离散

这里方差，标准差就不讲解了（平均差去掉绝对值的过程），注意一点，求样本方差和标准差时候自由度为n-1而不是n

5.离散系数（变异系数）

V=标准差/均值，特点；消除了数据水平不同和数据计量单位不同的影响，相当于归一化，常用于比较2种不同数据的离散程度

6.数据标准化

Z=（xi-平均值x）/S标准差，特点：判断一组数据是否有离群值，对某一数据在全体中的相对位置的度量

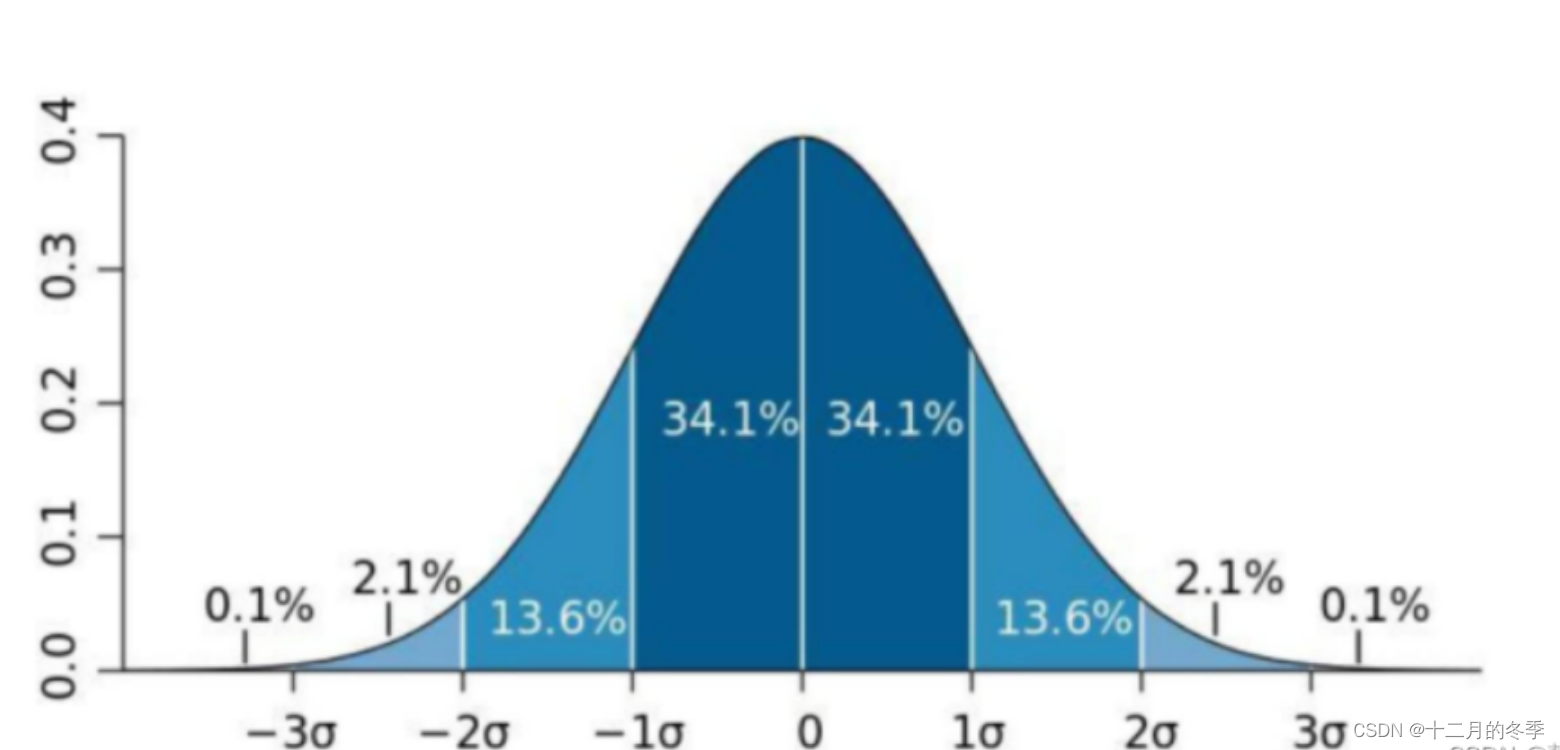
注意：当一组数据对称的时候，百分之68的数据在均值正负1倍标准差之内，百分之95数据在均值正负2倍标准差之内，百分之99的数据在均值正负3倍标准差之内，当一组数据不对称的时候，运用切比雪夫不等式：1-1/k的平方的数据落在平均数加减k倍标准差之内，k是任意大于1的数，k不一定是整数

7.偏态与峰态

这里的计算公式就不详细介绍了，考试基本不会考到，要是考到只能说倒霉了囧

偏态左偏分布性质：均值小于中位数小于众数，右偏分布：众数小于中位数小于均值

偏态和峰态最后算出来的绝对值正负0.5是轻微，0.5-1是中等，大于1是严重

8.统计分布

（1）两点分布与二项分布， E（x)=np，D（x）=np(1-p），n=1时为两点分布，若要求单个概率

（2）正太分布

概率密度：

当平均值为0，方差为1时为标准正太分布，概率密度为：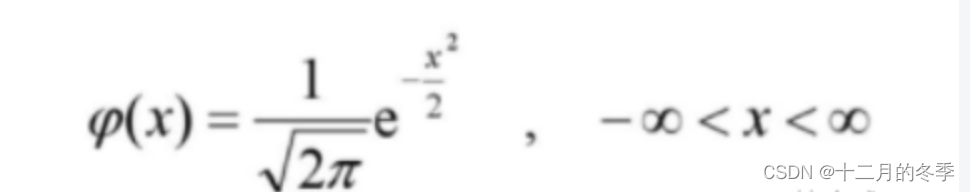

（3）卡方分布

表达式：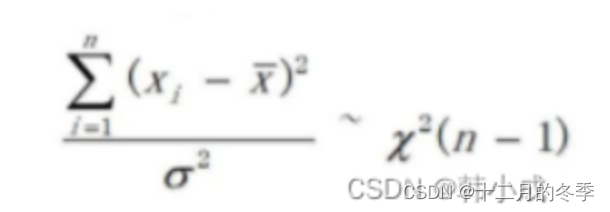

特点：

（4）t分布

表达式：t=X/（√（Y/n))，Y服从卡方分布

特点：

（5）F分布

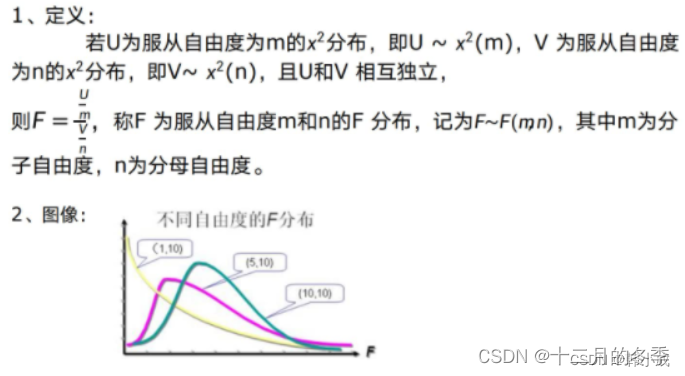
总结：F分布，t分布，卡方分布都属于抽样分布，用小样本估计大样本，当n越大越趋近正太分布

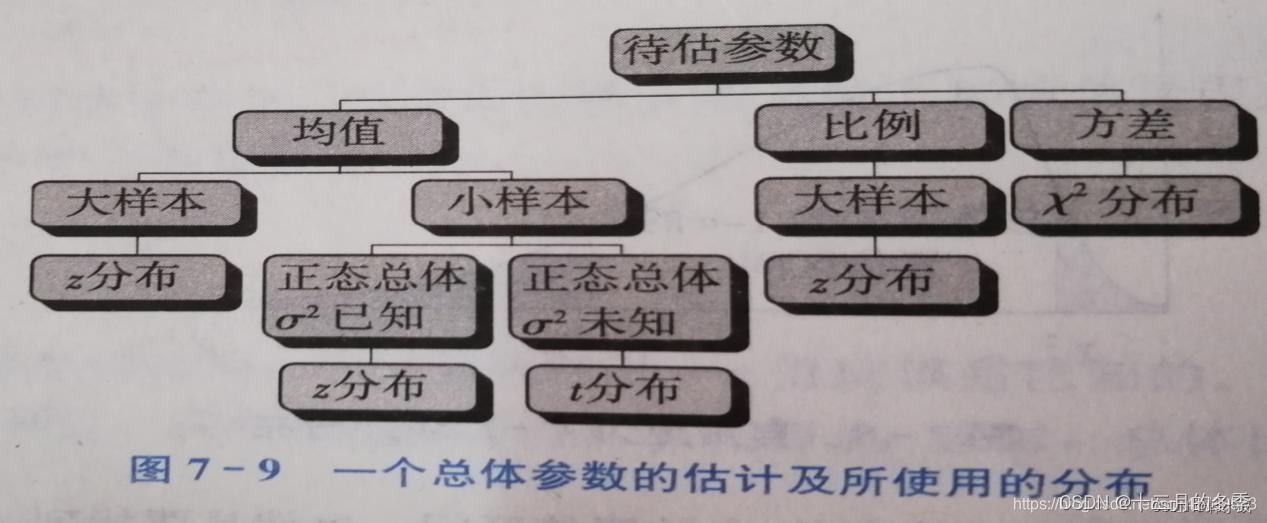
9.相关分析

当度量单位一致时：

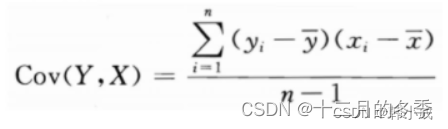
两个变量的相关性用协方差表示，协方差大于0为正相关，反之

当度量单位不一致时：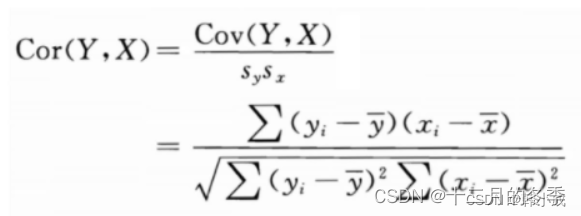

相关系数的取值在[-1,1]，当大于0时为正相关，反之；越趋近1越密切，越趋近0越不密切，r=0时为不相关（例如抛物线），特点：容易受离群值的影响

参数估计和假设检验的具体计算这里就不介绍了，在Level 1中不涉及这么难的题，若是遇到也没几分，只要把基本的概念理清楚就行了，祝大家考试通过
————————————————

–参考
原文链接：https://blog.youkuaiyun.com/qq_39971173/article/details/125657070