从信息论的角度看微博推荐算法

引言

在数字时代，推荐系统已成为社交媒体和其他在线服务平台的核心组成部分。它们通过分析用户行为和偏好，为用户提供个性化的内容，从而提高用户满意度和平台的参与度。推荐系统不仅能够增强用户体验，还能显著提升广告投放的效率和效果。随着技术的不断进步，信息论在推荐系统中的新兴应用逐渐显现，为推荐算法的优化提供了新的视角。
信息论是一门研究信息处理、存储、传输和通信的数学理论。其核心概念如熵、互信息和信道容量，为量化信息的不确定性、相关性和传输速率提供了理论基础。近年来，信息论在推荐系统中的应用逐渐增多，特别是在处理大规模数据和提高推荐质量方面显示出其独特的优势。

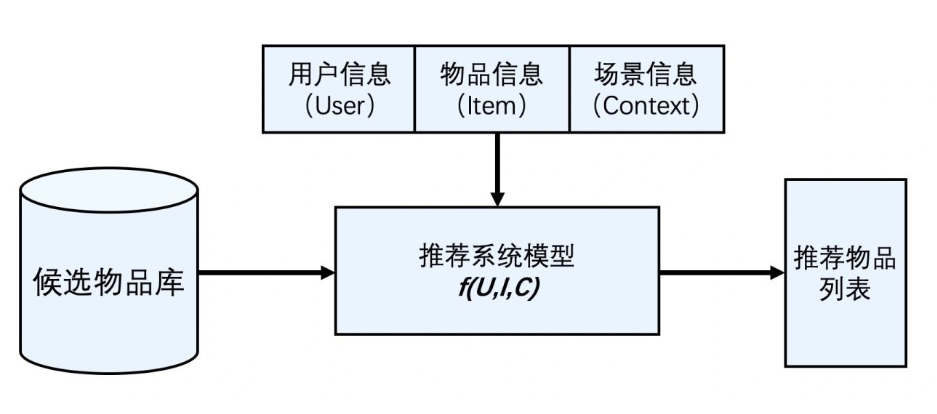
微博作为中国领先的社交媒体平台，拥有庞大的用户群体和丰富的内容生态。其推荐系统面临着诸多挑战，包括如何从海量内容中筛选出用户感兴趣的信息，如何在实时性要求下快速响应用户需求，以及如何在不断变化的用户行为中保持推荐效果的稳定性。本文将从信息论的角度探讨微博推荐算法实践，分析其在推荐系统中的具体应用和效果。

第一部分：信息论简介及在推荐系统中的应用

信息论简介

香农在其开创性著作《通信的数学理论》中首次提出了信息论。信息论的核心在于量化信息的不确定性和相关性。熵（Entropy）是衡量信息不确定性的度量，互信息（Mutual Information）则衡量两个信息源之间的相互依赖性，而信道容量（Channel Capacity）则描述了在特定信道下可以传输的最大信息量。当然，以下是信息论中几个核心概念的计算公式：

1. 信息熵（Entropy）

信息熵是衡量信息不确定性的度量。对于一个离散随机变量$(X)$ ，其概率分布为 $(P(X))$，信息熵$(H(X))$可以计算如下：
$H(X)=-{\sum }_{i}P(x_i){\log }_{2}P(x_i)$
其中，$(P(x_i))$ 是随机变量 $(X)$取第$(i)$ 个值的概率，$({\log }_2)$ 表示以2为底的对数。

2. 信道容量（Channel Capacity）

信道容量是衡量信道传输信息的最大速率的度量。对于一个离散无记忆信道，其信道容量$(C)$ 可以计算如下：
$C=$