本文是关于JavaScript算法基础的学习笔记，重点介绍了递归的基本概念和应用，如求和、求第N项的值。接着，文章探讨了二叉树的先序遍历实现，并引入了图的概念，包括邻接链表存储和深度优先、广度优先遍历。这些基础知识对于理解和运用递归及数据结构至关重要。
前言
注意： 本文不是新系列，只是学习算法时偶尔用到的笔记（刷题用的），不定期更新
这是一篇关于算法基础的文章，不涉及任何数学分析，只有最最基础的逻辑思维过程。大部分内容是个人理解，每个人想法自然迥异，欢迎讨论。
Q： Javascript里面有算法吗？
A： 有。
Q： 在哪？
A： 任何框架的源码里。
好了，言归正传吧。
开始：理解递归
关于递归，每本书的概念可能各不相同，有的细致、有的粗略，但表示的含义都是一致的，详细概念这里就略过，我在这里只做总结：
- 递归的关键点在于简化、归纳问题，而不是分解问题。
- 递归的本质是自己依赖自己，换言之，要能够分析自身过程的依赖规律。
下面给定两个例子，方便理解递归过程是怎样工作的。
注意：
下面的示例为实验参考，请不要在生产代码使用。
求和
给定一个数列：
1 2 3 4 5 6 7 … N
求 N项的和Sn。
假设n项的数列和为S(n)， 那么：
n=1 S(1) = 1 // 极限情形
n=2 S(2) = 2 + S(1) // S(2) 依赖于S(1)。
n=3 S(3) = 3 + S(2)
....
所以N项时，其规律为：
S(n) = n + S(n-1)
写成Javascript为：
// show 是一个工具函数
function show(...args){
let str = args.join(' ');
document.write("<p>"+str+"</p>")
}
// 正文
function sum(n){
if(n==1) return 1
return n + sum(n-1)
}
show(sum( 3 )) // 6
show(sum( 4 )) // 10
show(sum( 100 )) // 5050
求第N项的值
给定一个数列：
1 2 3 6 12 24 48 96 192 384 …
求第N项的值。
假设第N项的值为F(n)；那么：
n=1 F(1)=1 // 极限情形1
n=2 F(2)=2 // 极限情形2
n=3 F(3)= F(1)+F(2) = 3 // 多次依赖
n=4 F(4)= F(1)+F(2)+F(3) = 6
n=5 F(5)= F(1)+F(2)+F(3)+F(4)=12
... ...
伪代码：
f(n){
if n=1; return 1;
if n=2; return 2;
n2= n, sum=0
while(n2) sum+=f(--n2) // 多次依赖的时候，可以用循环
return sum
}
写成Javascript代码为：
function f(n){
if(n==1) return 1
if(n==2) return 2
let n2 = n, s =0
while(n2)
s+=f(--n2)
return s;
}
show(f( 3 )) // 3
show(f( 4 )) // 6
show(f( 10 )) // 384
okay， 基本上用数列入门递归是最简单的。记住这种感觉即可。
树
为简单起见，这里使用最简单的一种树——二叉树。
描述：
在二叉树中，，每个节点只能有一个父节点指向自己（根节点除外），每个节点至多只有两个子树（或树分支节点）。
假设创建节点两侧分支的过程为createTree (T,h), 其中，T是一个根节点，h是深度（或高度）计数，h=0时停止创建。 下面的抽象中，根节点是最深的。
当h=0时，
createTree (T,0)
return ;
附注：
- 相当于什么也不做，立即退出。
当h=1时，
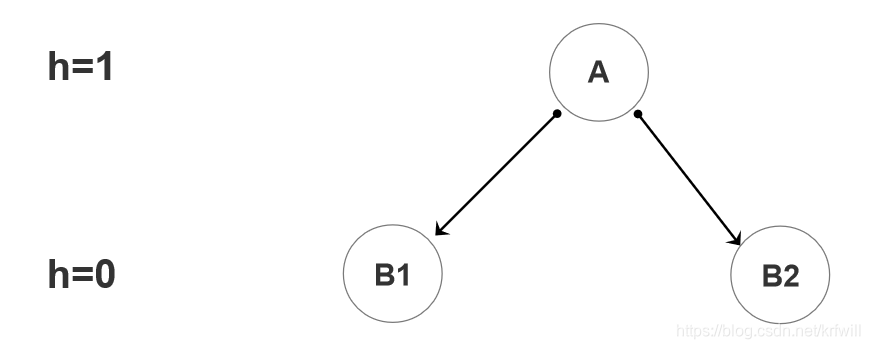
createTree (T,1)
创建T的两侧分支B1 B2
附注：
- 当
h=1时， 相当于为根节点建立左右两侧的分支B1、B2。
当h=2时，
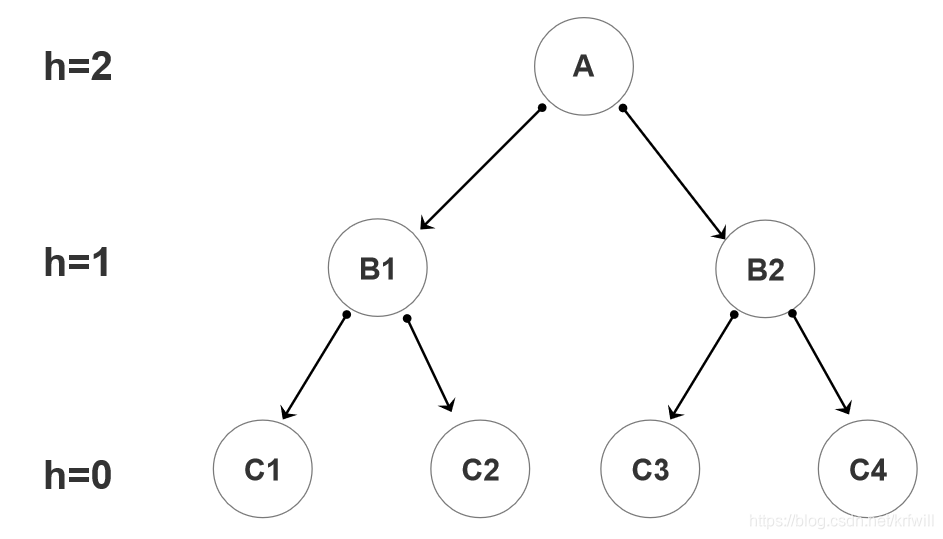
附注：工作流程如下：
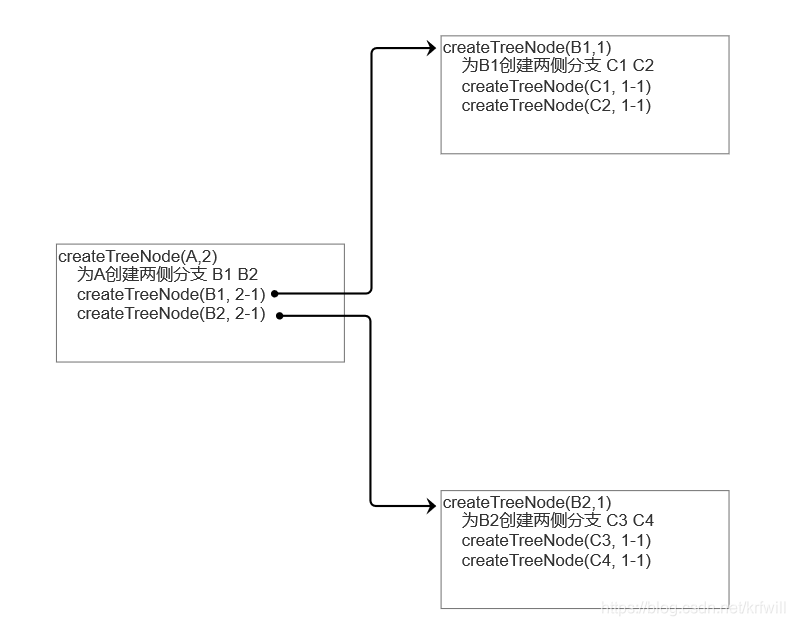附注：
- 当
h=0时，createTree()会结束。 - 当
h=1时，createTree(T)会只会创建T的两侧分支。
整理上面的过程，即：
createTree(A, 2)
创建A的两侧分支 B1 B2；
createTree(B1,2-1) // 创建B1的两侧分支， B1与A的深度不同， // 过程依赖1
// 当上个函数执行完毕后， B1的两侧分支完成。
createTree(B2, 2-1) // 创建B2的两侧分支 // 过程依赖2
当h=3时，树结构如下：
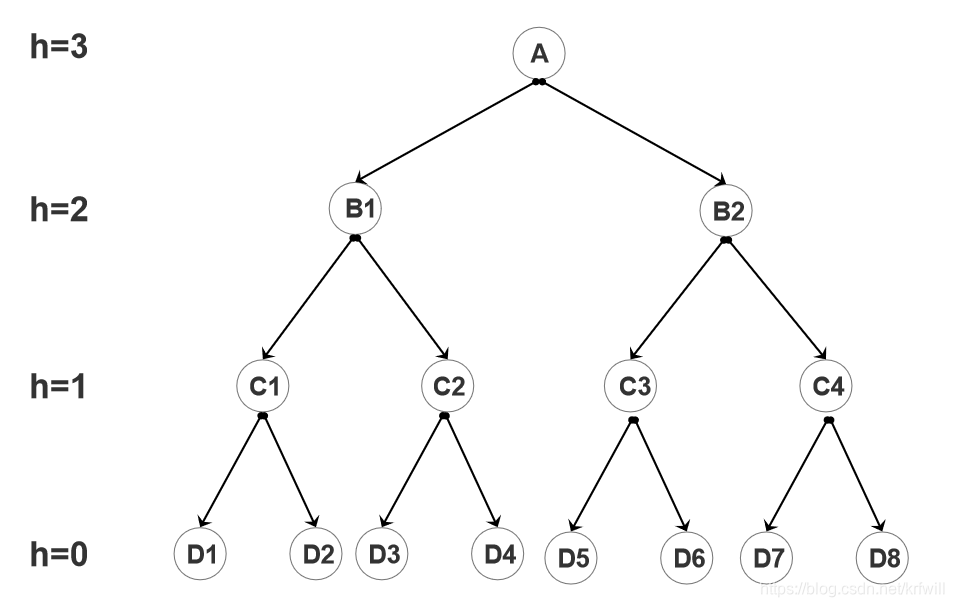工作流程图：
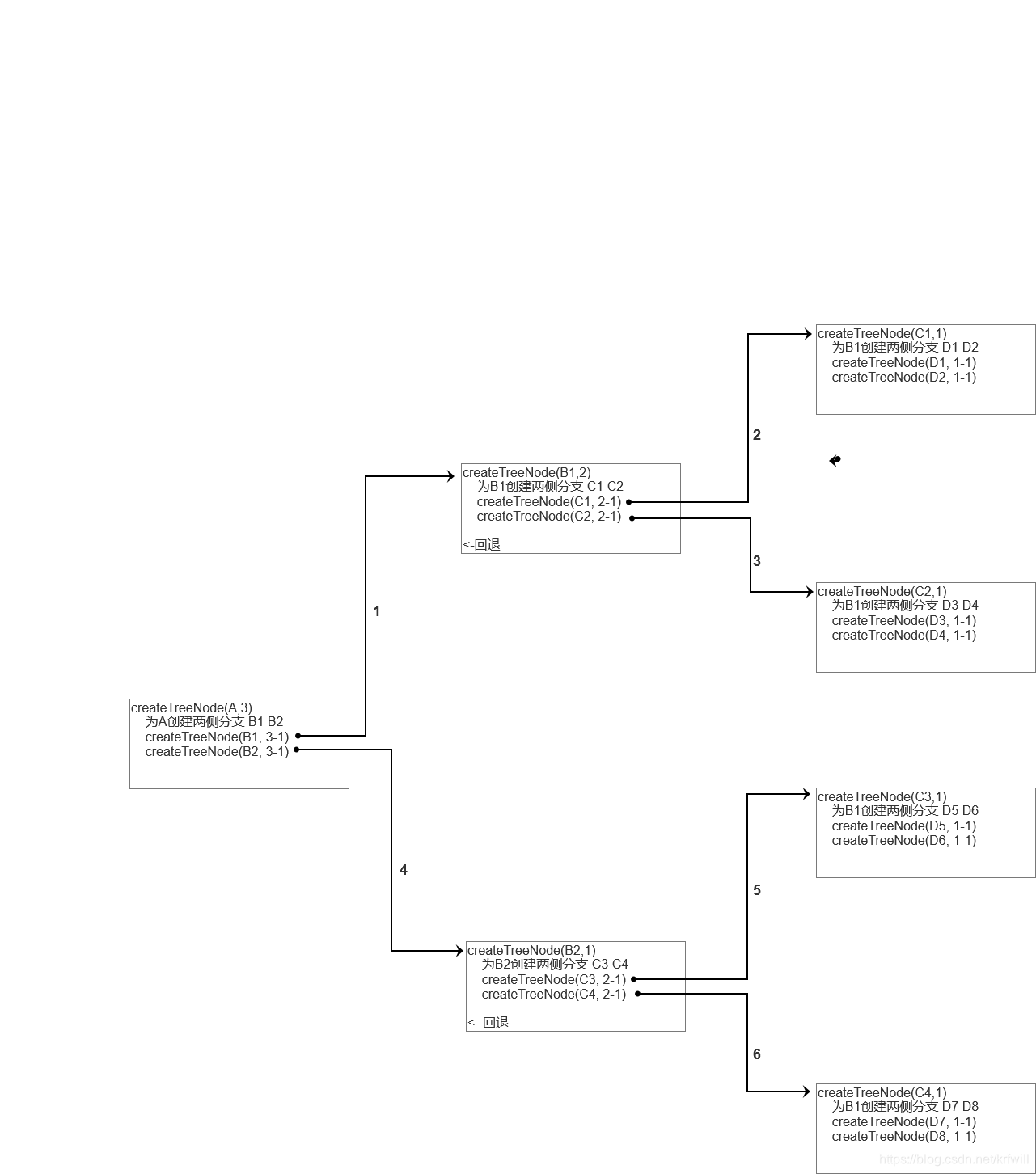
综上所述，如果h=N时，那么：
createTree (T,N)
创建T的两侧节点leftNode、rightNode
createTree (T.leftNode, N-1) // 过程依赖
createTree (T.rightNode, N-1) // 过程依赖
因此，写成Javascript代码后就是：
// 工具函数
function show(...args){
let str = args.join(' ');
document.write("<p>"+str+"</p>")
}
function initData(){
return parseInt(Math.random()*1000)%1000
}
var index= 0;
var visit = show;
// 正文
function TreeNode(){
this.id = index++
this.data = initData()
this.leftChild = null
this.rightChild = null
}
var root = new TreeNode() // 根节点
// T：树节点
// h：深度
function createTree(T, h){
if(h==0) return ;
T.leftChild = new TreeNode()
T.rightChild = new TreeNode()
createTree(T.leftChild , h-1)
createTree(T.rightChild , h-1)
}
仍然是简单起见， 这里只做一个先序遍历。
代码如下：
function preOrderTravel(root){
if(!root) return ;
visit(root.id, ' : ', root.data)
preOrderTravel(root.leftChild)
preOrderTravel(root.rightChild)
}
var root = new TreeNode() // 根节点
createTree(root,3)
preOrderTravel(root)
输出如下：
// 随机数！
0 : 438
1 : 646
3 : 906
5 : 523
6 : 540
4 : 604
7 : 505
8 : 990
2 : 250
9 : 591
11 : 427
12 : 657
10 : 118
13 : 492
14 : 146
小总结：
- 递归相当于完成当前过程中，需要依赖于之前的自身过程，找到依赖前后的状态非常重要。
- 这里的数据结构是最简单的，而且也不怎么规范，仅用于理解。
图
图也是最常见的一种数据结构，还是老规矩，省略概念，我这里只指出关键点，例如：
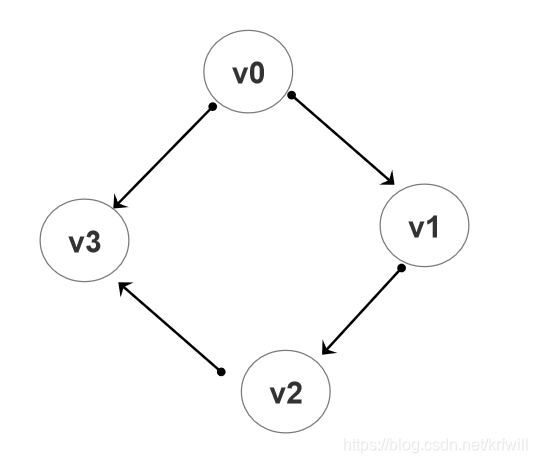上面是一个简单的有向图。重点如下：
- 如果
v1能够通过一条路径访问到顶点v2，那么就说v1和v2是连通，反之则是不连通的。 - 如果
v1和v2是连通的，那么之间的路径（它可以有方向）称作边。
图有很多种类，例如无向图、多重图、平面图等等。为便于理解，这里只使用最简单的有向图。
图有很多存储方式，例如邻接链表、邻接矩阵、邻接集合等等。在Javascript中，可以使用数组来模拟邻接链表存储方式。
邻接链表存储方式：
- 主链表是用于存放图中所有的顶点信息。
- 子链表是用于存放顶点周边的所有边的信息
上面的有向图，邻接链表存储后就是：
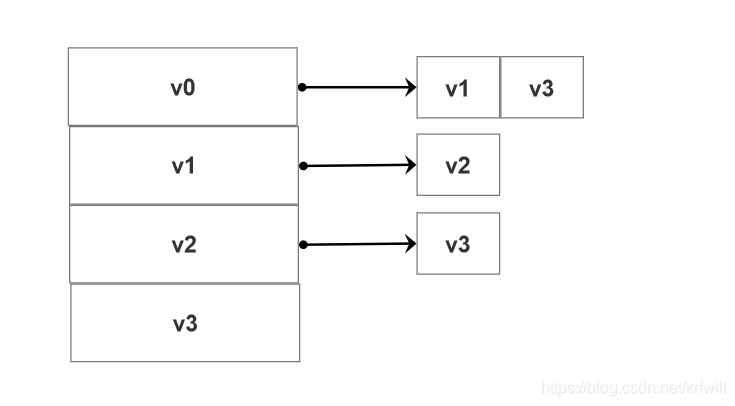
一个顶点Vertex构造信息如下：
function Vertex(){
this.id = index++ // 顶点ID
this.data = initData() // 顶点存放的数据
this.arcNodes = [] // 边信息
// 注意：
// arcNodes 实际上存放的是 Edge 数据结构，
// 但此处省略了大量细节（例如边的权重等）
// 所以arcNodes中实际上是周边连通顶点，特此说明。
}
然后再设置一个工具函数，用于连通两个顶点：
注意，连接两个顶点是单向连通的。
// p -> q
function connect(graph, p , q){
graph[p].arcNodes.push(graph[q]) //
}
最终，创建图的方法如下：
// graph: 图链表
// maps： 需要连通的顶点映射
// max： 图中的顶点最大数量
function createGraph(graph, maps, max){
for(let i = 0; i < max; i++)
graph[i] = new Vertex()
for(let i = 0; i < maps.length; i++)
connect(graph, maps[i].source, maps[i].target)
}
假定要创建下面的图：
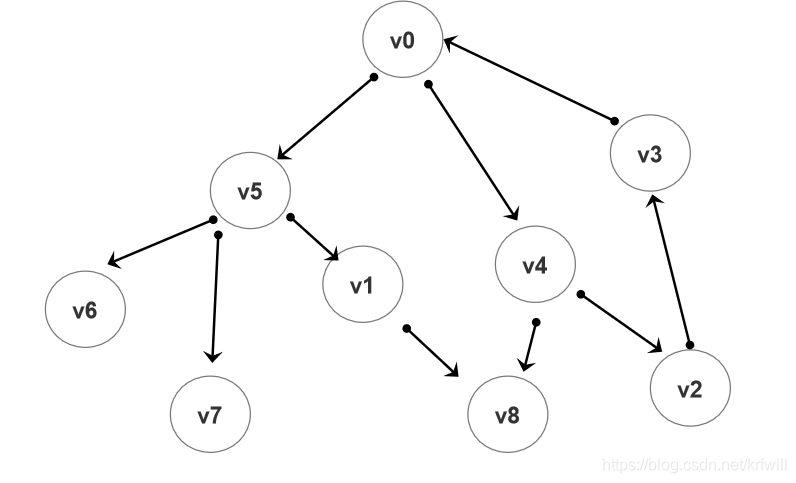
映射关联如下：
source target
0 5
0 4
5 6
5 7
5 1
1 8
4 8
4 2
2 3
3 0
即：
var maps= [ {source: 0, target: 5 },
{source: 0, target: 4 },
{source: 5, target: 6 },
{source: 5, target: 7 },
{source: 5, target: 1 },
{source: 1, target: 8 },
{source: 4, target: 8 },
{source: 4, target: 2 },
{source: 2, target: 3 },
{source: 3, target: 0 } ]
var graph = [] // 图
createGraph(graph, maps, 10)
图搞好了之后， 真正开始正文：
深度优先遍历
描述：
深度优先遍历的思想是从当前顶点层层深入，相对于当前顶点的顶点遍历，更优先于对当前顶点的周边连通顶点的顶点遍历。
就以这张图来说，深度优先遍历的策略就是：
v0->v5->v6 < ;
v0->v5->v7 <;
v0->v5->v1->v8 <<<
v0->v4->v8 <
v0->v4->v2->v3->v0
现在设深度优先遍历过程为DFS(g, v) ; 伪代码如下：
DFS(g , v)
0 访问当前顶点v，并将当前节点标记。
1 如果当前顶点v存在连通顶点（设为vN），那么：
1-0 如果 vN未被访问， 那么DFS(g, vN)
1-1 回到此层时，连通顶点vN的周边所有连通顶点必须遍历完成
1-2 回到`1`。
写成Javascript为：
function travel(g, v_id){ // g是图， v是当前顶点的id
let marks = [] // 如果顶点已经被访问，那么marks[v_id]设为true。否则为undefined。
function depthFirstSearch(g, v_id) {
visit(v_id, ' : ', g[v_id].data)
marks[v_id] = true
for(let vNode of g[v_id].arcNodes){
if(!marks[vNode.id])
depthFirstSearch(g, vNode.id)
}
}
depthFirstSearch(g, v_id)
}
travel(graph, 0)
show('------')
travel(graph, 1)
广度优先遍历
描述：
相较于深度优先遍历，广度优先遍历更优先于自身顶点的周边连通顶点的遍历。
如：
v0-> v5
v0->v4;
v5->v6;
v5->v7;
v5->v1;
v4->v8;
v4->v2;
v2->v3;
v3->v0;
function travel_bfs(g, v_id){
let marks = []
function breadthFirstSearch(g, v_id){
let queue = [ g[v_id] ]
// 将queue的顶点的周边连通顶点会被遍历。
visit(v_id, ' : ', g[v_id].data)
marks[v_id] = true
while(queue.length){
let [v] = queue.splice(0, 1)
for(let vNode of v.arcNodes)
if(!marks[vNode.id]) {
visit(vNode.id, ' : ', vNode.data)
marks[vNode.id] = true
queue.splice(queue.length, 0, vNode)
}
}
}
breadthFirstSearch(g, v_id)
}
show('------')
travel_bfs(graph,0)
最后
请一定要注意，这是关于算法基础的文章，不是深入，基本上算法的深度取决于逻辑思维，算法的掌控程度取决于数学思维（个人见解）， 因此如果希望深入算法学习的，一定会接触到高等数学， 逻辑和数学缺一不可。
Q： 为什么要用Javascript？
A： 不想用C++了……（懒癌）
扫一扫
364
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
