基于磁驱动的腹腔镜牵开器

基于局部磁驱动的腹腔镜组织牵开器

1 引言

腹部手术用磁性器械首次在 2007[1]被提出，旨在实现 与传统腹腔镜相同的三角定位（即腹腔镜中摄像头和手术器 械的三角形定位，类似于人体头部和手臂的位置关系[2]）， 同时显著降低侵入性。完全可插入工具通过磁性耦合穿过腹 壁，手术过程中不占用穿刺端口空间，并可通过单个标准腹 腔镜端口插入。通过移动患者腹壁外的外部磁体，可引导内 部装置到达适合操作的位置，从而在无需多个切口的情况下 实现所需的三角定位。

迄今为止开发的磁性外科器械包括摄像机[3], 、牵开 器[4], 、分离器[3], 和烧灼设备[5],，并通过单切口入路 在动物和人体模型上进行了试验[6]。

然而，由于外部控制磁体的手动操作导致灵活性较低且运动 精度较差，至今阻碍了磁性工具在复杂外科手术中的应用 任务，例如组织操作或精细可控的组织牵开。

解决灵活性受限的一个可能方案是将可控执行器嵌入磁 性器械内部。文献中报道的最常见方法是采用电磁（EM）电 机[7–9]。由于此类执行器可用的机械功率随质量和体积成比 例变化，能够通过单个微小切口的电机功率非常有限，无法 使外科医生完成提起器官等外科操作，也无法实时远程操作 器械尖端。

另一种方法是通过患者体外的磁场发生器与体内器械之 间进行无束缚传输机械能。这种方法可以实现受控运动，而 无需内置电机。Dupont及其同事的研究[10]展示了这一方 法，其中利用磁共振成像扫描仪产生的磁场驱动受限的小型 铁磁体绕垂直轴旋转。该旋转体连接到一个齿轮箱，用于控 制针头注射机器人。类似的方法也见于参考文献[11],，其中 利用永磁体产生的外部旋转磁场驱动植入式伸缩杆，以矫正 骨骼畸形。

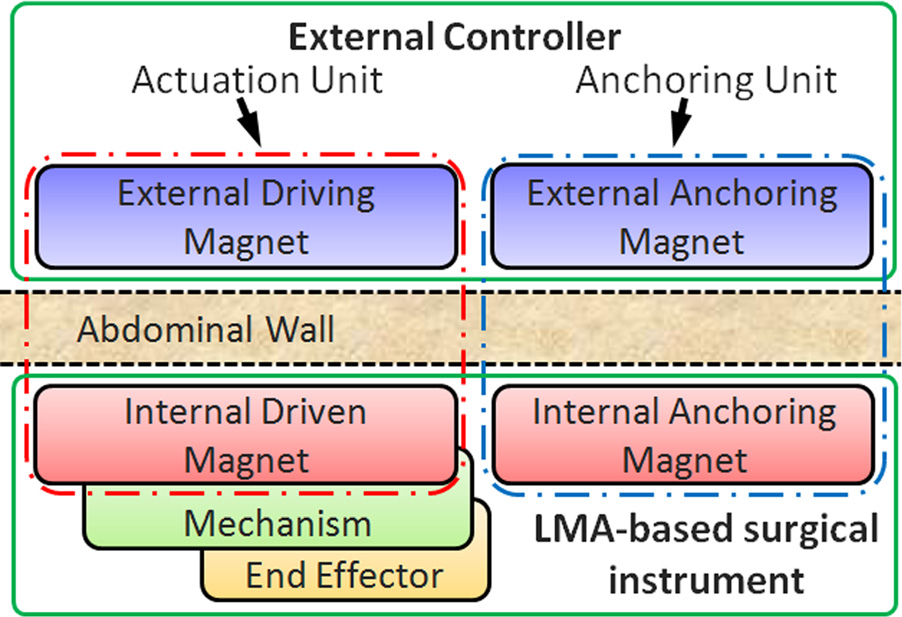
过去，我们曾提出将类似的概念应用于腹部手术，即引 入LMA方法[12,13]。如图1所示，基于LMA的装置由至少一 个锚定单元以及每个独立自由度对应的驱动单元组成 自由度（DoF）需要被控制。锚定单元由外部和内部永久锚 定磁铁（EAM和IAM）组成，其功能是在手术期间支撑器 械。驱动单元由外部驱动磁铁和内部从动磁铁（EDM和 IDM）组成。EDM通过电机进行轴向旋转，从而引起I DM的旋转。传递给IDM的机械功率（以旋转速度和负载扭 矩表示）随后可用于驱动机构，而无需使用嵌入式电磁电机。

该方法的主要优点是，可以在患者体外使用大而强大的电机， 通过磁耦合将机械功率传递到腹腔内部。

在本研究中，我们首次介绍了LapR‐LMA，一种基于 LMA方法的腹腔镜组织牵开器。该器械仅由机械部件组成， 因此可实现高压灭菌，并可在无需专用切口或内置电机的情 况下，对器官进行可控的牵开。除了描述LapR‐LMA之外， 本研究还展示了在开发和测试新型基于LMA的腹腔镜器械时 应采用的设计流程。

2 临床考虑

基于LMA的腹腔镜器械的设计涉及外部控制器和手术工 具的开发。该系统的这两个部分的主要设计规格可从以下临床 考虑中得出。

2.1 穿刺端口

腹腔镜手术通常通过在腹壁上放置三到四个套管针来完成。内径最大的套管针通常专用于内窥镜摄像头 （例如，柯惠医疗VersaportV2的内径为13mm，马萨诸 塞州曼斯菲尔德）。假设我们使用该端口进行插入，则可将 12.7mm视为基于LMA的器械的最大外径[9]。直径的限制会 影响手术工具内部所有组件的设计，包括内部磁铁。

2.2 腹部厚度

磁场强度随着患者体外磁铁与体内磁铁之间距离的增加而呈指数级下降。因此，腹部厚度在磁体选择中 起着关键作用——特别是对外部磁铁而言——因为仪器内部的 磁铁已受到进入通道直径的限制。在充气状态下，该值通常在 20mm至40mm之间。 假设腹部组织厚度，以包含超重患者（体重指数高达30kg/m2）[14]。

2.3 安全性

稀土永磁体可产生强吸引力，存在对位于外部 和内部磁铁之间组织造成组织学损伤的风险。贝斯特等人在猪模 型中报道，46.7千帕的压力是完全可以耐受的。我们将此值视为 基于LMA的器械在运行过程中不应超过的安全阈值。

2.4 灭菌

为了便于低成本再处理，可重复使用外科器 械应能承受蒸汽灭菌常用的高温（即 132 C[15]）。这排除 了在器械上使用电子元件的可能性，并要求选用特殊等级的 永磁体。

2.5 内部工作空间

腹腔内窥镜手术通常通过向腹腔内充 入二氧化碳来实施。根据Beckerman和Ma[16]的报告，作 为可插入器械应具备长度的一般指导原则，我们可以将腹壁 与干预点之间的最大距离假设为275毫米。这为器械应能到达 的工作空间提供了参考，同时也对器械长度提出了限制。

2.6 外部工作空间

外部控制器必须紧凑且易于外科 医生使用，通过磁拖动实现内部装置的粗略定位。达到所需定 位后，应在LMA驱动单元运行时将控制器锁定在位置上。

2.7 易用性

为了最大限度地提高未来应用的潜力，手 术器械必须易于引入腹腔，且外部控制器应操作直观。一旦 证明了所提出方法的可行性，外科医生的反馈对于改进设计 的人机工程学就变得至关重要。

尽管上述考虑事项可应用于任何基于LMA的腹腔镜器械， 但以下内容特指组织牵开器。

2.8 自由度

组织牵开需要一个可控的自由度，以抬高或 降低被操作的器官。该自由度不应可逆驱动，以便在外科医 生在下方操作时保持组织处于牵开状态。器官被牵拉的速度 并非关键要求，只要耗时与手术流程相容即可。

2.9 牵开力

可以假设牵开器末端执行器[17]所需的目标力 至少为5牛顿。该目标值在胆囊切除术中的肝脏牵拉和胆囊暴露 过程中是典型的。在机构操作以抬起组织时，必须动态地提供该 力的大小，并且在静态下也能维持，从而允许外科医生在其下方 进行操作。有趣的是，迄今为止报道的使用嵌入式电磁电机的可 插入式牵开器[8,18]最多只能产生1.53牛顿的力。

2.10 与被牵开组织的交互

如果待牵开的组织不会被切 除，则手术工具在与其交互时必须温和。此时可以采用吸盘 [19]或扇形杠杆[3]。另一方面，如果外科医生计划在手术 过程结束时切除被牵开的组织（例如胆囊切除术），则创伤 性抓钳（如鳄鱼钳）[4]是一种可行的解决方案。

3 操作原理

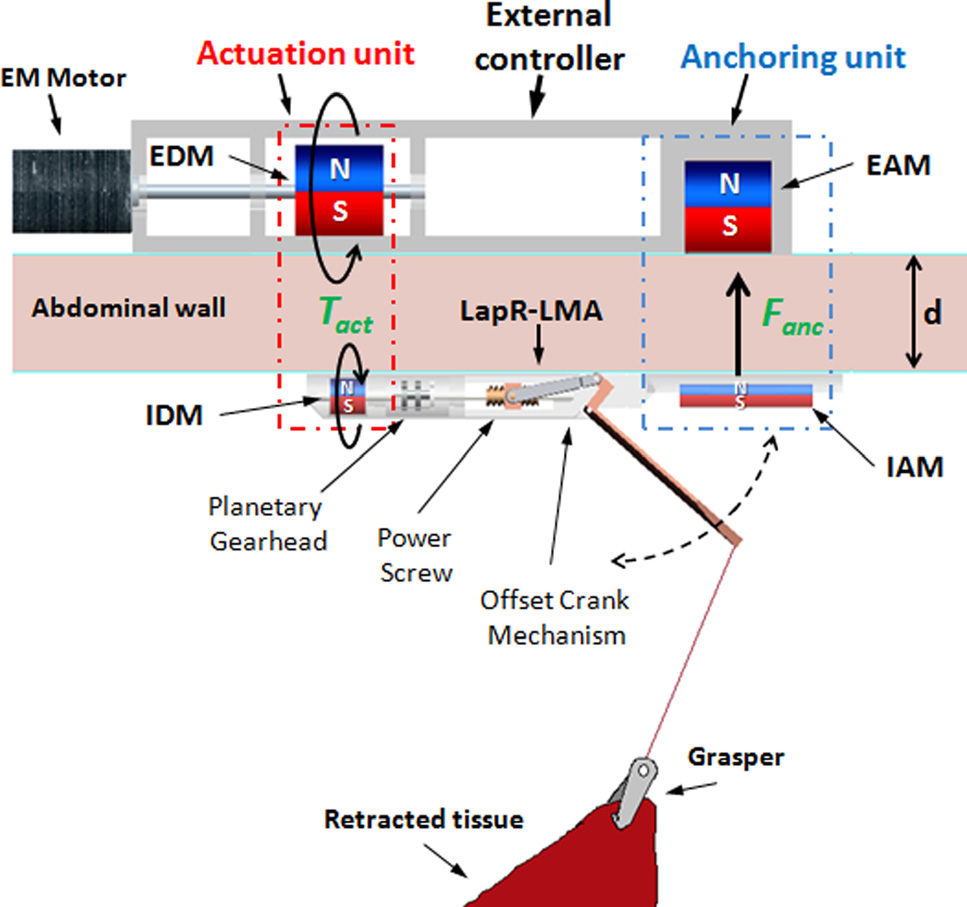
鉴于上述临床考虑，我们提出了基于LMA的组织牵开器， 其示意图如图2所示，并将其称为LapR‐LMA。

锚定单元主要负责粗略定位以及支撑装置和回缩组织， 而驱动单元则设计用于将外部电磁电机的机械功率传递到 LapR‐LMA内部的机构。

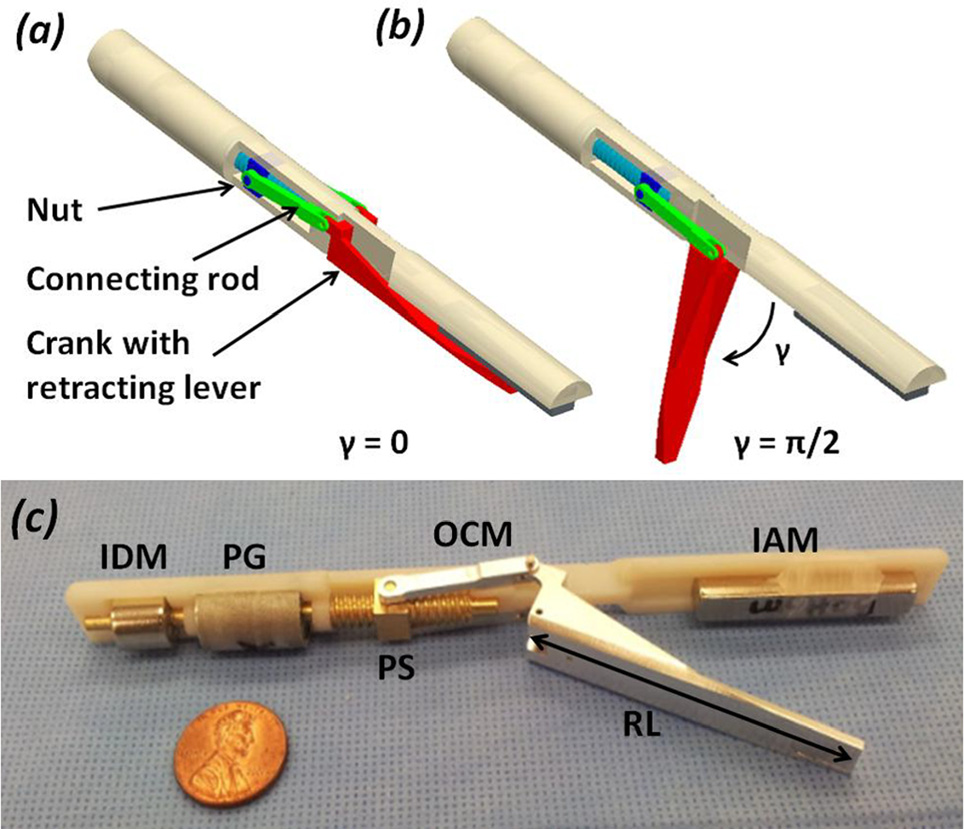
IDM的旋转运动传递给一个定制的机械传动链，该传动 链的设计旨在最大化抓钳处的提升力，并符合前一节中规定的 尺寸限制。具体而言，IDM连接到一个三级行星齿轮箱（ PG），驱动一个带动偏置曲柄机构（OCM）的丝杠（PS）。

OCM控制回缩杠杆的角位置。为了评估所提出的设计方案， 我们通过一根不可伸长的线将鳄鱼抓钳连接到杠杆上。正如 Padilla等人[4],所述，外科医生可以使用标准腹腔镜镊子将 抓钳夹持在目标组织上。如果特定应用需要无创抓钳，可改用 吸盘[19]或扇形末端执行器[3] 。

4 LapR‐LMA平台的设计

4.1 磁学设计

在锚定和驱动单元的建模与设计过程中， 通过有限元分析（FEA）（COMSOL MUL-TIPHYSICS 4.3b，瑞 典），采用DiNatali等人提出并验证的方法，对磁力矩和力 进行了估算。具体而言，有限元分析仿真基于稳态电流、永 磁体和磁路分析所使用的理论与方法[20]。

在估算磁性单元的不同贡献时，我们假设锚定单元和驱动单 元之间的距离足够远，可以忽略串扰效应。这一假设的有效性在 台架验证期间得到了验证（第5.1节）。本研究中使用的所有永磁 体均购自宾夕法尼亚州皮珀斯维尔的K&JMagnetics,Inc.。

4.1.1 锚定单元

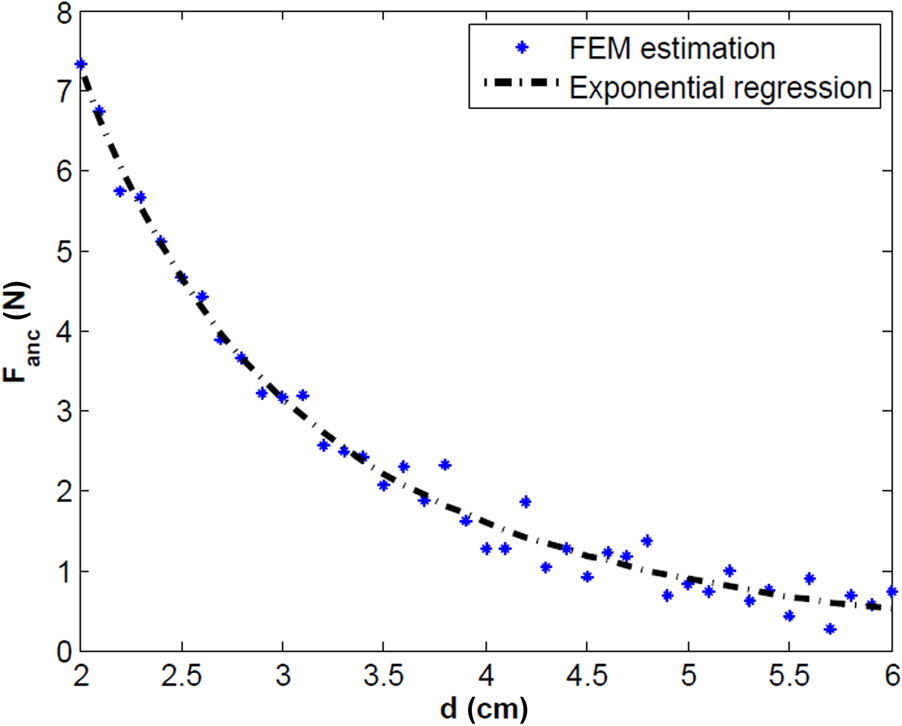
LapR‐LMA必须具有圆柱形以进入手术端 口。因此，IAM可用的空间具有圆形横截面。这表明应使用圆 柱形磁铁。然而，正如Agashe和Arnold[21],所报道的，方形 横截面的永磁体比圆柱形磁铁具有更强的耦合作用。因此，选择 了一个长度为38毫米、边长为6.35毫米的永磁体，以适配在 LapR‐LMA内部。该永磁体由钕铁硼（NdFeB）制成，磁化等 级为N52，方向如图2所示。一个边长为25.4毫米的立方体 NdFeB磁铁 并选择N52磁化（1.48T磁剩磁）作为EAM，以在本研究考 察的磁体间分离范围内，在IAM上实现足够的吸引力Fanc。给 定两个选定的锚定磁铁，通过使用包含超过3,500,000个单元 的网格进行有限元分析模拟，并将磁体间分离距离Fanc估计 为d从2厘米到6厘米以0.1厘米增量变化。需要指出的是，所研 究的范围大于第2.2节中提到的范围，以便提高结果的可信度 并获得更可靠的回归。如图3所示，数据拟合为双项指数函数 （R2> 0.94）。

4.1.2 驱动单元

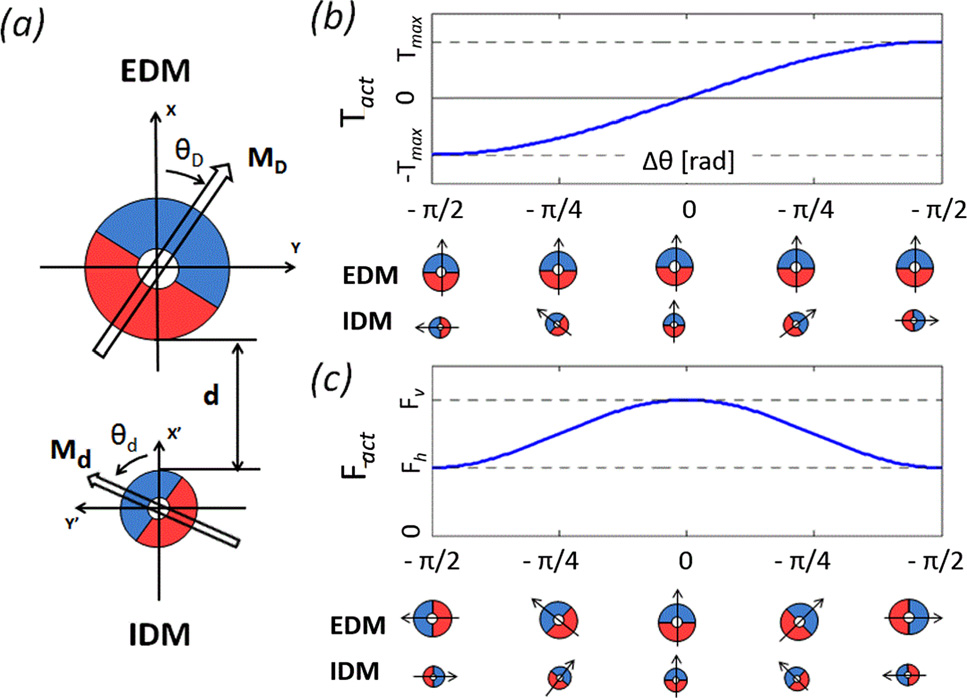
该驱动单元基于磁性直齿轮[22] 的概 念，由两个径向磁化的环形磁偶极子组成，即EDM和IDM， 它们可绕平行轴自由旋转。参考图4(a)，我们定义MD和Md 分别为EDM和IDM的磁化矢量，hD和hd为MD和Md的角坐 标，d为EDM与IDM外表面之间的最短距离。通常，我们假 设d与LapR‐LMA和外部控制器之间的间距一致。两个角坐标 之差决定了驱动单元的角位移Dh¼ hD hd。图4(a)中y轴与 y0轴采用相反的方向，以强调EDM的顺时针旋转会导致I DM的逆时针旋转。

如图4(b)所示，从EDM传递到IDM的扭矩Tact是点D# [12,23,24]的函数，如下所示：
$$
T_{act}(D#) = T_{max} \cdot \sin(D#)
$$
其中Tmax是磁耦合能够传递的最大扭矩。Tmax取决于 EDM和IDM的体积、磁化强度以及它们之间的距离d。如果| 点D#|超过p/2，磁耦合将进入失步状态，导致随之而来的 失控，如Montague等人所述[25]。在第4.3.1节中，我们估 算了LapR‐LMA能够提升最大负载时对应的点Dhmax 。由于 第4.2节所述三级机构引入的机械优势，点Dhmax远低于失步 阈值。

EDM与IDM之间的磁耦合还会在两个磁铁之间产生垂直吸 引力。该力称为Fact，通过与Fanc协同作用，有助于支撑回缩组织。

如图4(c)所示，Fact可表示为h D的三角函数，从而得到
$$
F_{act}(D#) = F_v + \frac{F_h}{2} + \frac{F_v - F_h}{2} \cdot \cos(2D#)
$$
其中，Fv和Fh分别为驱动磁铁垂直和水平排列时Fact的最大 值和最小值。与Tmax类似，Fv和Fh的值取决于EDM和ID M的体积、磁化强度以及它们之间的距离d。此外，Fv和Fh 是Dh的函数。尽管图4(c)中的曲线图考虑了Dh¼ 0，但在第 4.3.2节中，我们将讨论Fv和Fh在范围|Dh| <Dhmax内的变化 情况。

所选IDM的外径（OD）为9.52毫米，内径（ID）为 2.38毫米，长度（L）为9.52毫米。它由钕铁硼制成，相对磁 导率为1.05，磁化等级为N42（1.32T剩磁）。EDM的外径 （OD）为25.4毫米，内径（ID）为6.32毫米，长度（L）为 25.4毫米，且具有与IDM相同的磁特性。

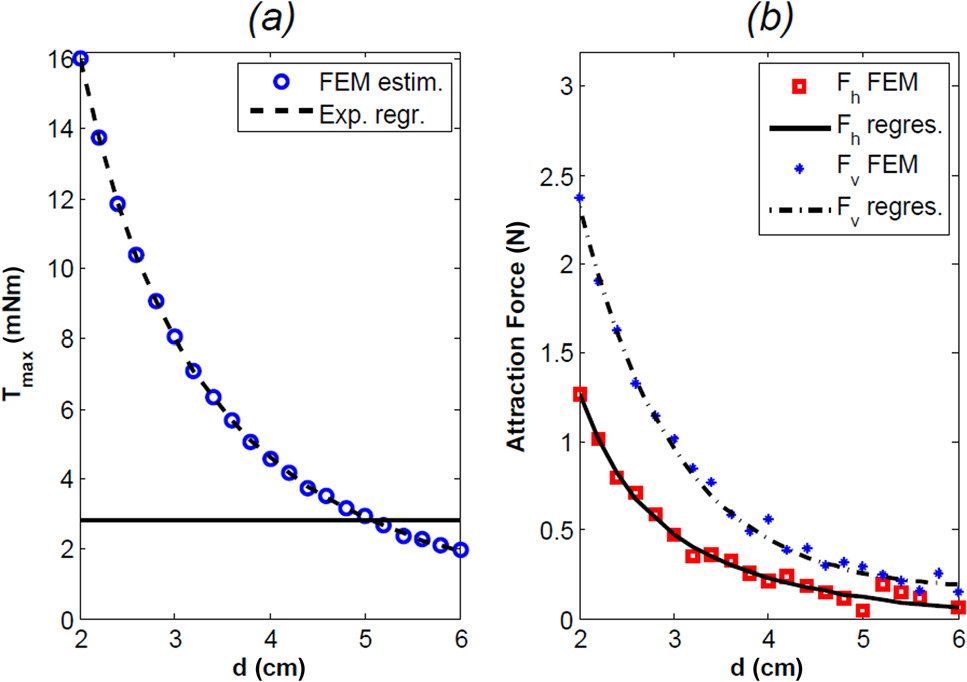
根据所选的两种磁铁，我们进行了一系列有限元分析仿真，以预测 Tmax、Fv和F h 作为d的函数关系。在估算Fv和F h 时，我们假设了Dh¼ 0。 该假设的影响在第4.3.2节中进行了讨论。在有限元分析仿真中，我们使 用了包含超过3,500,000个单元的网格，并将d从2厘米到6厘米以0.2厘 米递增进行变化。仿真结果以及对数据进行指数回归拟合的结果分别在 图5(a)中针对Tmax和图5(b)中针对Fv和F h 进行了报告。

从图5(a)可以看出，有趣的是，与体积与IDM相似的电磁电 机相比，只要d保持在5cm以下，可用于驱动机构的转矩就更大。 [26–28],。

考虑到从EDM到IDM的速度比为1:1，能够提供给腹腔内 机构的总机械功率主要取决于驱动EDM旋转的外部电机的转 速。由于尺寸在选择外部执行器时并非主要限制因素，因此 一个足够强大且快速的电机可以轻松超过嵌入式电磁电机所 能提供的机械功率，后者因需适配12毫米手术通道而在尺寸 上受到限制。

4.2 机械传动设计

4.2.1 行星齿轮箱

机械传动的第一级由一个具有三级结构且传 动比为1:64的行星齿轮箱组成 (GRpg)。环形齿圈（图6(a)中的点A）和整个PG的外径为11毫米， 长度为17毫米。对于每一级，载荷通过行星轮从太阳轮传递到环 形齿圈。行星轮数量越多，每个行星轮与环形齿圈之间界面处的 局部应力就越低。因此，为了优化系统的承载能力，我们通过在 每级使用四个行星轮来最大化行星轮数量。太阳轮（图6(a)中的 点S）和行星轮（图6(a)中的点P）设计为具有10个渐开线齿形、 0.32模数、22.5度压力角、3.2毫米节圆直径和3.125毫米厚度。 零件采用铝6061‐T6材料（抗拉强度—屈服276MPa；抗拉强度— 极限310MPa；相对磁导率1.004）通过电火花加工制造。

采用直径为0.8mm的不锈钢销将太阳轮与行星架（图 6(a)中的点C）连接，而采用直径为2mm的销来装配行星轮。 三级行星齿轮箱的各个单个部件如图6(a)所示，而装配后的 单级结构如图6(b)所示。

行星齿轮效率通过图7所示的定制台架试验进行表征。采用 激光切割结构固定电磁电机（2342S‐024CR，Faulhaber，德 国），该电机连接至行星齿轮输入太阳轮。一个双通道光学编码 器（HEDS5500，安华高科技公司，圣何塞，加利福尼亚州）， 每转96个脉冲，连接到电磁电机上以测量输入角速度xin。行星 齿轮输出行星架连接至磁滞制动器（H3，PlacidIndustries， 莱克普拉西德，纽约州）。在试验过程中，通过基于PC的工作 站以电流控制制动器，逐步增加输出扭矩sout。

通过监测电磁电机消耗的电流，测量了电磁电机施加到行 星齿轮箱输入端的扭矩（称为sin）。类似地，通过监测磁滞制 动器消耗的电流得到sout。输出速度xout通过将一个径向磁化永 磁体连接到输出轴，并利用静态霍尔效应传感器（CY‐P15A， 辰阳科技，芬辛，德国）测量磁场旋转来测得。

行星齿轮效率，定义为
$$
\eta_{pg} = \frac{\tau_{out} \omega_{out}}{\tau_{in} \omega_{in}} \times 100\%
$$
通过在1700转/分钟下使用恒定的xin，同时在15秒的时间内 将sout从0毫牛·米增加到80毫牛·米进行实验得出。该试验重 复了三次，平均效率为61.25%至63.16%。

关于承载能力，行星齿轮工作范围是通过刘易斯方程根据安全齿载 荷估算得出的
$$
W = \frac{S \cdot F \cdot Y}{D_p}
$$
其中W（牛）为安全齿载荷，S为材料最大弯曲应力，F为齿 轮齿宽，Dp为径节，Y为刘易斯齿形系数。考虑1.6毫米的节 圆半径和四行星轮结构，估算出行星齿轮安全输出扭矩（Tsafe） 为134.96毫牛·米。

4.2.2 丝杠

设计了一种带单线螺纹的丝杠，与一个7毫米 方螺母配合使用。该丝杠的节圆直径dm为4.8毫米，长度为25毫 米，导程P为0.2725毫米/弧度，牙型角#为30度，螺旋升角a为 18.3度。螺母厚度为6毫米，其运动用于驱动OCM。丝杠与 OCM之间的连接通过放置在螺母侧面的2毫米销钉实现。

丝杠部件采用黄铜制造（抗拉强度—屈服310兆帕；抗拉 强度—极限476兆帕；磁导率1.05）。

为实现力Fnut，需施加到动力螺杆上的扭矩sr可通过以下公式估算：
$$
\tau_r = \frac{d_m \cdot F_{nut}}{2} \left( \frac{l_s + \cos \theta \cdot \tan \alpha}{\cos \theta - l_s \cdot \tan \alpha} \right) + \frac{d_{mc} l_c W}{2} = \frac{W}{b_{ps}}
$$
其中，dmc表示螺母支承面平均直径，ls表示螺杆与螺母之间 的静摩擦系数，lc表示支承面的静摩擦系数，bps为动力螺杆 在输入扭矩与输出力之间的传递函数。由于采用了低摩擦的 缩醛树脂轴承，支承面摩擦被忽略不计。根据设计的几何参 数以及干态黄铜对黄铜的静摩擦系数（即ls¼ 0.1[29]），bps 的结果为0.9117N/mNm。

动力螺杆的效率gps通过举重测试进行评估。之前实验中 使用的电磁电机被刚性连接到动力螺杆上。在螺母上施加从 0.4535千克到4.5349千克、以0.4535千克为增量的重量，并 通过监测供电电流测量电磁电机提升该重量所需的扭矩smot。

对于每个重量，进行了三次试验，并在假设螺母速度无 损耗的情况下（即螺母速度Vnut通过动力螺杆的导程P由电机 转速xmot估算），使用以下公式计算平均效率gps：
$$
\eta_{ps} = \frac{F_{nut} V_{nut}}{\tau_{mot} \omega_{mot}} \times 100\% = \frac{F_{nut} P}{\tau_{mot}} \times 100\%
$$
效率gps结果为69.85±5.44%。

4.2.3 偏置曲柄机构（OCM）

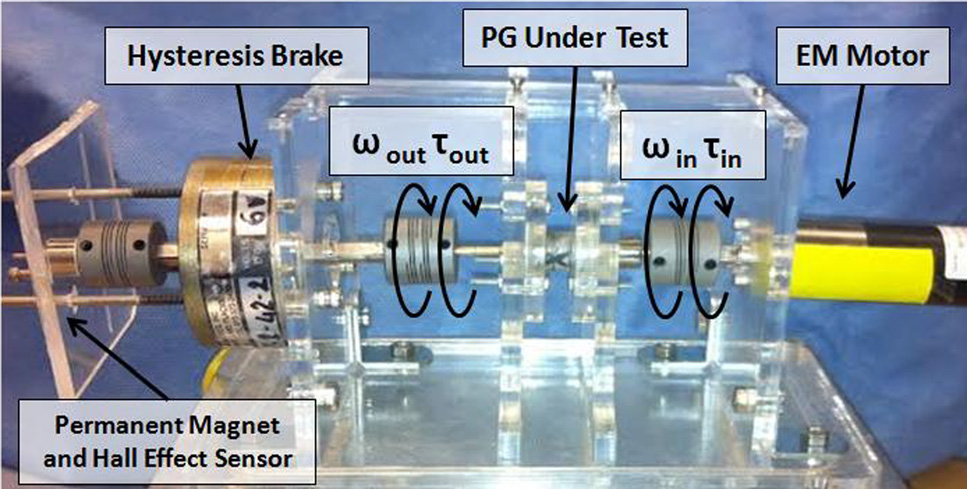
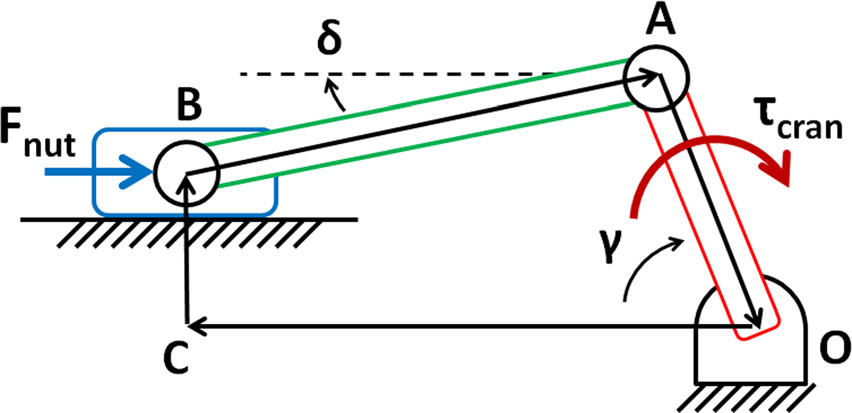
机械传动链的最后一个 组件是操作回缩杠杆的OCM。通过确定OCM连杆尺寸、初始 构型以及所需的运动范围，可在曲柄角p/2处实现总角位移c。 集成在OCM中的回缩杠杆因此可产生等于其自身长度的回缩 组织总垂直位移。通过准静态分析，假设螺母运动缓慢且连 杆惯性可忽略，我们定义了OCM机械伪优势C—单位为 mNm/N—作为曲柄机构输出扭矩scran（见图8）与作用在滑 块上的相应输入力Fnut之间的比值。根据图8中的示意图，我 们可以将C表示为c的函数，如下所示：
$$
C(c) = \frac{\tau_{cran}}{F_{nut}} = AO \cdot \sin(c) + AO \cdot \cos(c) \cdot \tan(d)
$$
其中，角度c在初始构型（回缩杠杆闭合）时定义为零，当 回缩杠杆完全打开时为p/2。考虑到OC（螺母水平位移）是 单自由度OCM系统的输入参数，角度d可通过求解关于OC 的方程组表示为c的函数：

4.2.3 偏置曲柄机构（OCM）（续）

$$
c = 2 \tan^{-1} \left( \frac{-2 \cdot AB \cdot BC - \sqrt{(-2 \cdot OC \cdot AB)^2 + 2 \cdot AB \cdot BC^2 - OC^2 + BC^2 + AB^2 - AO^2)^2}}{-2 \cdot OC \cdot BA - OC^2 - BC^2 - BA^2 + AO^2} \right)
$$

$$
d = 2 \tan^{-1} \left( \frac{-2 \cdot AO \cdot BC - \sqrt{(-2 \cdot OC \cdot AO)^2 + 2 \cdot AO \cdot BC^2 - OC^2 + BC^2 + AO^2 - BA^2)^2}}{-2 \cdot OC \cdot AO - OC^2 - BC^2 - AO^2 + BA^2} \right)
$$

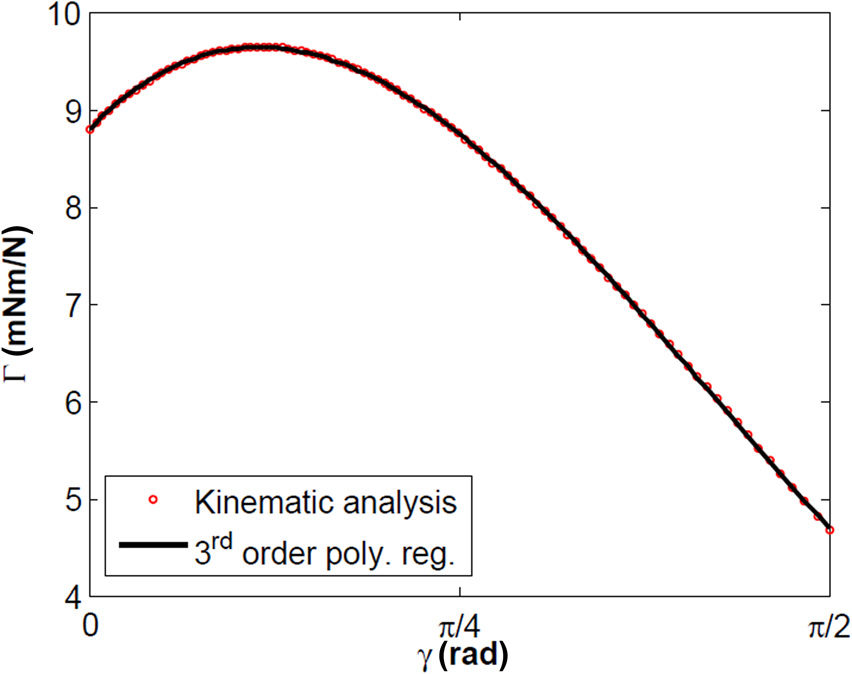
两连杆的长度（即AB = 25 mm，AO = 9.43 mm）以及滑块 相对于铰链点的偏移量（即BC = 4 mm）可在滑块移动 12.7mm时提供p/2的角位移。当杠杆角c变化时，机械伪优势 C —通过迭代计算获得，假设惯性可忽略且处于准静态状态— 如图9所示，并附有其三阶多项式回归（R² = 0.990）。

OCM部件采用6061‐T1铝合金（抗拉强度—屈服55兆帕； 抗拉强度—极限120兆帕；磁导率1.004）通过传统机械加工 制成。使用直径为1毫米和1.5毫米的不锈钢销连接部件。

4.2.4 附加组件与系统集成

LapR‐LMA 装置主体采用快速 成型技术（Objet 30 pro，Stratasys，以色列雷霍沃特）使用 Vero White + 塑料制造，用于嵌入上述组件。外径设定为 12.5毫米，以防止机械失效。装置主体分为两半制造，以便于内 部组件的装配。机械传动链的对中由 Delrin® 平面轴承（6毫米 外径，3毫米内径，3毫米长）保证，该轴承具有低摩擦和高耐磨 性。

使用了两根连杆将OCM与PS连接，从而平衡螺母运动并 将传递力分散，以降低配合部件之间的内部应力。回缩杠杆 设计为与两根连杆配合，并在装置主体的铰链点处旋转。回 缩杠杆长度（RL）为58.5毫米，可在整个跨度c范围内实现 约6厘米的总垂直组织位移。杠杆设计中的加强筋可防止其弯 曲。

在当前版本的LapR‐LMA中，OCM和PS暴露在外，以验证 试验过程中的运动情况。未来，它们可以被封装在设备的外壳内。

如图 10 所示，机械传动部件围绕设备核心的厚实挤出部 分排列。该特征可确保LapR‐LMA的结构强度。

制造的原型，如图 10(c) 所示，长度为154毫米，直径为12.5毫米， 重量为39.16克。

4.3 LapR‐LMA建模

在LapR‐LMA的主要组件设计完 成后，开发了两个简单的模型来预测整体性能。 一个初步的数学模型，旨在通过磁耦合可传递的扭矩以 及各子模块的效率，来估算该设备的组织提升性能。该模型 还可用于预测与夹持器处重量相对应的角位移Dh。 我们开发的第二个模型是LapR‐LMA的受力分析图。该 模型可用于预测锚定单元和驱动单元提供的磁吸引力能够静 态支撑的重量。

4.3.1 组织提升模型

假设由于内部摩擦不产生功率损耗，则 在EDM旋转启动时可提升的重量WL(g)可预测如下：

$$
W_L <
\begin{cases}
\frac{10^3}{9.8} \cdot \frac{T_{act} \cdot GR_{pg} \cdot \eta_{pg} \cdot b_{ps} \cdot \eta_{ps}}{RL \cdot C(c)}, & \text{if } T_{act} < T_{safe} \cdot GR_{pg} \cdot \eta_{pg} \
\frac{10^3}{9.8} \cdot \frac{T_{safe} \cdot b_{ps} \cdot \eta_{ps}}{RL \cdot C(c)}, & \text{if } T_{act} > T_{safe} \cdot GR_{pg} \cdot \eta_{pg}
\end{cases}
$$

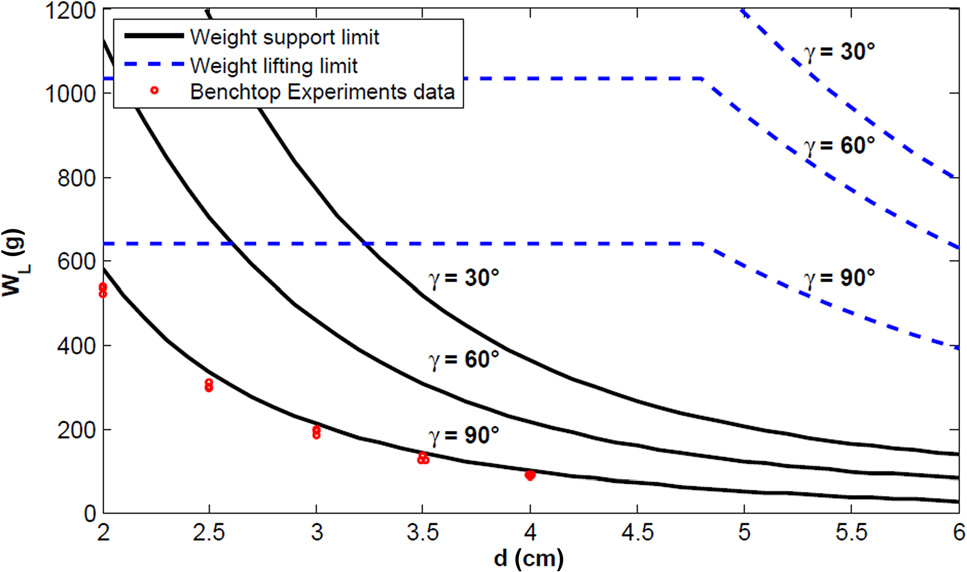
如图 11 中蓝色虚线所示，WL在 d 上保持恒定，只要 Tact 超出 行星齿轮箱 PG 的安全齿载工作区间（公式 (4)）。在此工作区间—— 涵盖第 d 从 2 cm 到 4 cm 的整个范围，如第 2 节所规定——机械传 动链的整体效率为 42.78%。在此区域的大部分范围内，角位移 Dh 保持在 p/18（即 10度）以下，因此我们可以假设 Dhmax = p/18。还 值得一提的是，随着 WL 和机械传动链效率的提高，c 从 p/2 变为零， 这得益于图 9 所示的 OCM 贡献。这对于进行可控回缩是一个优势， 因为在组织（及其重量）被提升时，其重量部分也随之增加。

4.3.2 组织支撑模型

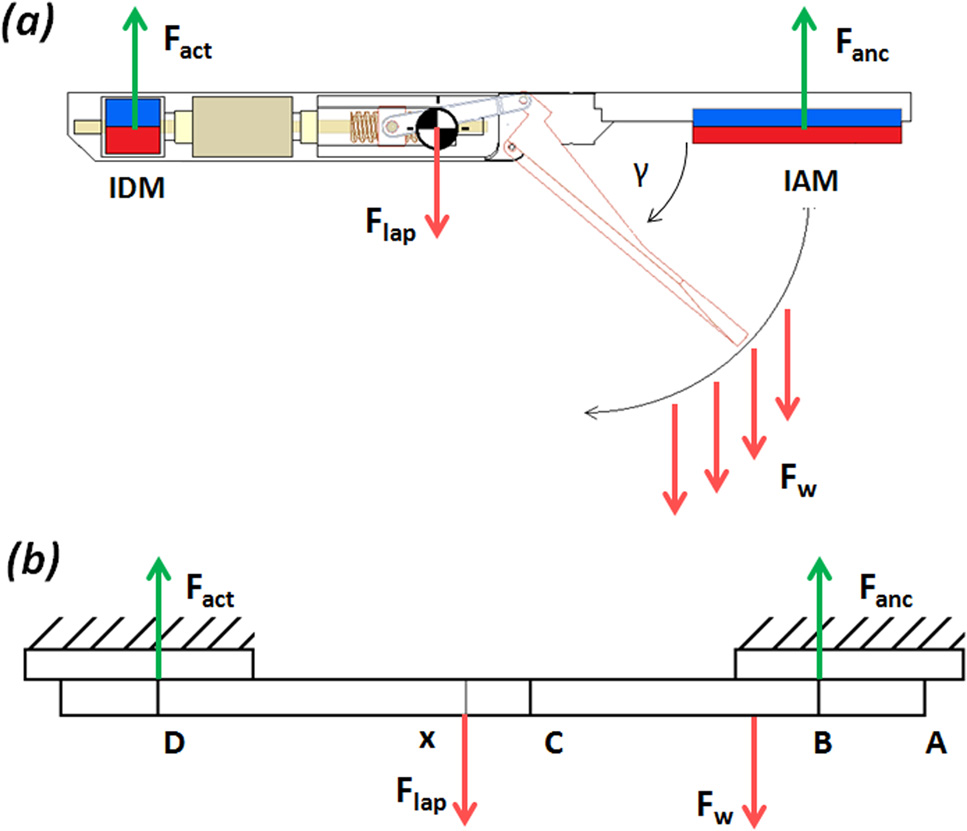
为了预测LapR‐LMA在不同d和c 条件下静态地所能支撑的重量，我们研究了如图12所示的装 置的受力分析图。

该模型考虑了第4.1.1节中描述的Fanc、作用在LapR‐LMA上的 重量力Flap，以及在夹持器处提升重量WL所需的力FW。该模型还 考虑了第4.1.2节中描述的Fact，但根据Dhmax = π/18进行了缩放。 在 |Dh| < π/18 的情况下，我们通过有限元分析模拟估算出Fh和Fv 相对于图5(b)中报告值的变化低于2.7%。

在我们的结构模型中，装置主体被假设为一根梁，作用 于IAM和IDM上的磁力负责将LapR‐LMA锚定在腹壁上（此 处腹壁被视为刚性约束）。力Fw被假定向下作用在一个位置 取决于杠杆角坐标c的点上。如图12(a)所示，LapR‐LMA的 设计使得Fw始终作用于Fanc和Fact作用点之间（见图12(b)中 的点B和点D），从而在可控回缩过程中提高稳定性。

由于 Fanc在任何情况下都大于 Fact —如图 3和 5(b)所示—当 LapR‐LMA围绕靠近内锚磁体的边缘（即图12(b)中的点A）旋转时， 最可能发生锚定失效。特别是当c = p/2 时为最不利情况，因为此时 Fw作用于杠杆铰链点（即图12(b)中的点C），其相对于点A的力臂达 到最大。

稳定锚定的条件可以通过考虑点A处的旋转平衡来表示，即

$$
F_W < \frac{F_{Anc} \cdot AB + F_{act} \cdot AD - F_{lap} \cdot AX}{AC}
$$

其中Flap是提升LapR‐LMA所需的力，X是LapR‐LMA质心的位置。 该稳定性条件在图11中以实心黑线表示，显示了 LapR‐LMA能够静态支撑的最大重量WL随d和c变化的情况。

同样，在此情况下，当c从p/2减小到0时，性能得到提升， 因为FW的作用点更靠近旋转点（即图12(b)中的点A）。

通过将组织提升和组织支撑模型绘制在一起，如图 11 所示，我们可以得出LapR‐LMA的工作范围，即同时能够被支 撑并提升的最小WL值以下的区域。

考虑到LapR‐LMA的几何特征以及工作范围内锚定力的 数值，该装置对腹壁施加的压力始终低于30.7千帕，因此满 足第2节中规定的安全条件。

4.4 外部控制器

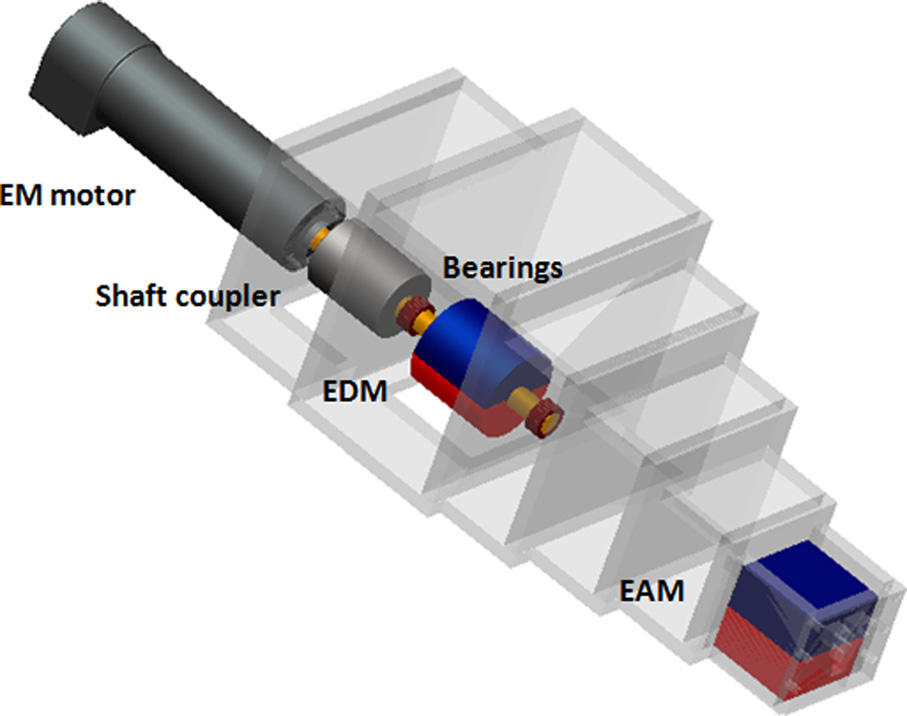
外部控制器设计用于在塑料手柄中安装 EDM、EAM和电磁电机（2342S‐024CR，Faulhaber，德国）。 通过激光切割和组装有机玻璃板，制成了具有五个空腔的形状， 操作员可将手指插入其中。

如图 13 所示，EDM通过轴联轴器与电磁电机刚性连接。 轴承用于支撑轴。EDM与EAM之间的间距与LapR‐LMA内 部IDM和IAM的定位相对应。

一个双态开关连接到电机控制器，用于改变EDM的旋转 方向。这使得能够在提升和下降与抓钳相连的组织之间进行 切换。

一种可调节的离合臂——未在图13中示出——可连接到控 制器，以在手术过程中固定控制器的位置。

5 实验评估

采用三级验证方法来评估LapR‐LMA的性能。首先进行了台式 实验 进行了实验，以验证该装置在不同磁体间分离距离下可控制 地提起并保持的重量。随后，使用新鲜切除的猪组织进行离 体实验，以研究利用LapR‐LMA进行肝脏牵拉的可行性。最 后，在猪模型中通过腹腔镜手术方式重复了相同手术过程， 以评估该装置的可用性和安全性。

5.1 台式实验

本实验的主要目标是验证第4.3节中估算的 LapR‐LMA的工作范围。如图14所示，外部控制器固定在 垂直可调的滑块上，并通过一个刚性塑料表面与LapR‐LMA连接。重量通过一根不可伸长的线连接到杠杆上——起始 位置为c = p/2。然后以1700转/分的速度向外部电磁电机发出 阶跃指令并启动。当c达到零时，旋转方向反转，杠杆回到起 始位置。每次试验中成功提升和下降的最大重量被记录下来。

该试验在磁体间距离从2 cm到4 cm、以0.5 cm为增量的每个 距离下均进行了三次，结果如图11所示。

在点D = 2厘米处提升500克重量的试验如图15所示。本实验的总体 结果表明 图11中的模型始终高估了WL，误差为9.06 ± 0.52%。这可能 是由于在建模LapR‐LMA时忽略了锚定模块与驱动模块之间 的串扰效应所致。

在试验过程中，当 c = p/2 时总是发生失效，装置失去与 外部控制器的磁耦合（即锚定失效）。驱动模块始终正常运 行，从未进入极滑移状态。这证实了 Dhmax 较小的假设。完成单次试验的平均时间为 41.65 ± 2.11 秒。最后，台式实验 确认所设计的机构不具备可逆驱动性，因为杠杆能够在 c = 0 时保持其位置。

5.2 离体试验

外科牵开器的典型任务是提升肝脏并将其固 定在适当位置。胆囊和胃位于其下方。为了暴露这些器官并 获得足够的手术操作空间可视性，外科医生通常需要抬起肝 脏右叶。该手术过程使用第5.1节中描述的相同装置进行模拟， 但用一头新鲜切除的猪肝（672 g）代替了重物。肝脏放置在 距离塑料表面15 cm的位置。一个鳄鱼抓钳通过一根不可伸长 的线连接到LapR‐LMA的杠杆上，并固定在肝脏的一个叶上。

牵拉操作从c = p/2 开始，对应距离 d = 2 cm（图16(a)）和 d = 4 cm（图16(b)）。电磁电机以1700转/分钟运行。每种距 离进行了三次试验，肝脏均被成功地提升和放下。从图16中 的帧可以看出，在牵拉过程中被悬吊的组织部分逐渐增加。

如前所述，当c从p/2减小到零时，LapR‐LMA的提升和支撑 能力随之增加，从而补偿了这一变化。

5.3 体内试验

体内试验的主要目标是在麻醉猪模型上 定性评估LapR‐LMA的功能性、可用性和安全性。特别是， 在外部控制器与LapR‐LMA之间存在可变形组织时，牵开器 会在变化的F act 作用下在垂直方向产生振动。这种垂直摆动可 能会影响提升和锚定能力 而磁性夹持可能会对位于外部控制器和LapR‐LMA之间的组织造成安全 风险。

手术过程在范德比尔特大学进行，并由经过专门培训的 医疗团队协助完成（IACUC批准号M/2014/163），严格遵 守所有动物实验相关的伦理考量和法规。本研究使用了一头 55公斤雌性约克夏猪。在静脉镇静后，通过一个5毫米穿刺 器（5 Versaport Plus，柯惠医疗，康涅狄格州诺沃克）和 一个12毫米穿刺器（5‐12Versaport Plus，柯惠医疗，康涅 狄格州诺沃克）建立微创入路。将LapR‐LMA引入腹腔并与 外部控制器连接。在外科医生插入端口前，在穿刺点测量到 腹部厚度为2厘米。随后使用二氧化碳气体建立气腹。

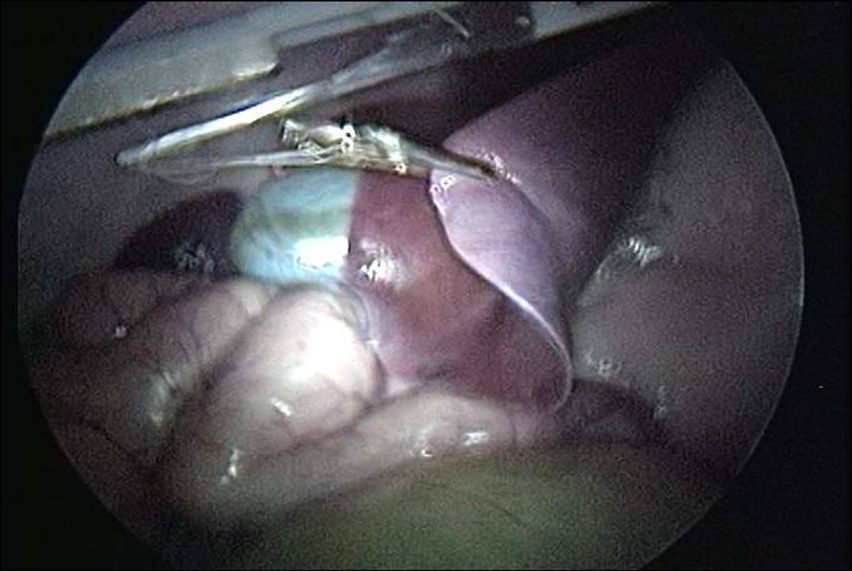
在内窥镜视野下，手动操作外部控制器，将LapR‐LMA拖动至肝脏附近。外科医生使用标准腹腔镜抓钳将鳄鱼钳 固定在肝脏的一个叶上。然后通过旋转驱动磁铁启动牵拉， 直至暴露肝脏下方的组织，如图17所示。该手术过程重复五 次，每次均改变LapR‐LMA的位置以及肝脏被抓钳固定的点。

手术过程结束后，动物被处死。位于腹壁组织的区域 LapR‐LMA在牵拉期间被固定，随后被切除并由专家病理学 家检查，报告显示由于磁力夹持导致的组织损伤迹象。

尽管牵拉操作始终成功，且LapR‐LMA从未与外部控制 器失去磁耦合，但设备的长度有时会妨碍其在腹腔内的活动 性。这使得LapR‐LMA的位置只能在动物的矢状面附近几度 范围内调整，无法将其放置于横向方向。这限制了可达工作 空间以及对需牵拉组织的可接近角度。

6 结论与未来发展方向

磁场可用于将可控的机械动力从患者体外传递到体内的 腹腔镜器械。通过结合具有不同功能（即锚定或驱动）的磁 性单元，可以设计出无需内置电机且在手术过程中不占用穿 刺孔空间的手术机器人。

鉴于微创手术器械在直径和体积上的限制，所提出的方 法能够传递比在器械上嵌入典型机电执行器更大的机械功率。 同时，由于采用了磁耦合，三角定位得以增强，并且侵入性 降低。

在本研究中，我们验证了使用LMA方法设计无缆腹腔镜 组织牵开器的可行性。相同的設計步驟（即與磁耦合相關的 醫學考量和技術要求、磁建模、磁體選擇、IDM與機械傳動 鏈之間的介面，以及整體設備性能的建模）可用於實現執行 不同且更複雜任務的基於LMA的手术机器人。

LapR‐LMA 的直径为 12.5 mm，可通过腹腔镜引入。 如果腹壁厚度约为 2 cm，LapR‐LMA 能够牵拉超过其自身 重量十倍的负荷。台架试验表明，所设计的机构不具备可逆 驱动性，能够保证牵开杠杆在两个方向上的运动准确且可控。 该机构能够在约 20 秒内完成全运动范围。尽管其运动速度与 手动操作腹腔镜牵开器相比更慢，但外科医生能够精确调节 LapR‐LMA 实现的牵拉程度。如果需要更短的时间，可将外 部控制器中的电机更换为更快的型号。

在过载情况下，失效发生在锚定而非驱动部分。如果发 生锚定失效，外科医生在手术过程中需要将LapR‐LMA重新 连接到外部控制器。然而，在腹壁组织厚度为2厘米的猪模型 上进行的肝脏牵拉实验中，未观察到任何失效情况。同一实 验也显示，由于磁力夹持未造成腹壁组织损伤。

尽管本研究显示了有希望的结果，但未来研究仍面临许多挑战。

关于LapR‐LMA建模，可提升的最大重量被高估了约9 %。这主要是由于假设锚定单元与驱动单元之间不存在交叉 耦合。因此，必须建立一个更全面的模型，以捕捉设备中所 有磁铁之间的相互作用。锚定单元与驱动单元之间的距离越 近，它们之间的交叉耦合就越强，因此，为了设计更短版本 的LapR‐LMA，建立更精确的模型至关重要。缩短设备长度 将提高操作性，并改善对手术目标的可达性，这一点在体内 试验中已得到证实。

由于本研究的主要目标是评估通过LMA方法可实现的机 械功率传递，因此我们并未广泛关注与设备相互作用的部分 需要被牵拉的组织。特别是，由于创伤性抓钳易于获得，肝 脏牵拉是使用创伤性抓钳进行的。但这不适用于临床病例， 在临床病例中必须使用吸盘[19]或扇形末端执行器[3]以防 止损伤肝组织。当前版本的LapR‐LMA可在手术过程结束时 需要移除被牵拉组织的情况下使用（例如胆囊切除术）。尽 管当前设备为无线设计，但可以引入一条细的有线连接以方 便在手术结束时回收设备。未来将开展涉及外科医生的研究， 以评估并根据需要改进该设备的可用性和人机工程学。

嵌入LapR‐LMA中的永磁体可使其磁性保持至 80 °C。如 果需要进行高压灭菌，则必须更换为更昂贵的磁铁——仍可从 同一供应商获得——能够耐受高达 150 °C的温度。另一种方案 是将LapR‐LMA设计为一次性使用装置。如果机械部件实现 批量生产，该装置的总成本可能降至几美元。

关于制造材料，LapR‐LMA主体通过使用Vero White +塑料进行快速成型获得。在进入临床试验阶段后， 必须使用生物相容性材料。该主体可分别采用数控加工或注 射成型来制造，以作为可重复使用或一次性器械的一部分。

通过使用具有更高磁化等级或更大体积的外部永磁体，可以在 更远距离获得更强的牵引力。所提出的建模方法可用于选择适合特 定需求的磁铁，有可能将这种方法的应用范围扩展到肥胖患者。

最后，一个引人关注的未来研究方向是设计一种具有多自由度 的基于局部磁驱动的手术机器人。这种设备将能够完成复杂的外科 手术任务，例如使用光学探头进行表面扫描，甚至实现缝合。在一 个可适用于腹腔镜通路的设备中集成多个驱动单元和一个或多个锚 定单元，需要先进的建模技术，以及很可能在单元之间使用屏蔽材 料[30]。