基于UCB的能效优化算法

在能量收集无线传感器网络中学习优化能量效率

摘要

我们研究了能量源向多个能量收集节点进行无线功率传输，以最大化能量效率的问题。在每个时隙中，源节点使用可用的功率等级之一向节点传输能量，而节点则利用收集的能量将信息传回能量源。源节点没有任何信道状态信息，仅知道从特定节点接收到的码字是否成功解码。在该有限信息条件下，源节点必须学习能够最大化网络能量效率的最优功率等级。我们将该问题建模为一个随机多臂赌博机问题，并设计了一种基于上置信界的算法，用于学习使能量效率最大化的能量源最优发射功率。数值结果验证了所提算法的性能保证，并显示出相较于基准方案的显著增益。

索引词

多臂赌博机，能量收集，无线供能通信网络，能量效率

I. 引言

无线供电通信网络（WPCN）中的节点能够进行能量收集（EH），近年来作为一种下一代无线网络的潜在技术引起了广泛关注。通过从周围环境或专用能源中获取能量，EH有助于持续为无线节点的电池充电，从而延长无线节点寿命。当使用专用能源进行能量传输时，其发射的能量需要适当校准。一方面，由于能量收集设备可采集能量的基本限制，高功率发射可能导致能量浪费；另一方面，低功率发射可能导致能量收集设备无法采集到足够的能量。因此，能量源必须以合适的功率进行传输。由此，以比特每焦耳为单位的能量效率（EE）度量作为优化WPCN中发射功率的关键性能指标，受到了广泛关注。受此启发，本文的目标是开发一种算法，用于学习最大化WPCN中能量效率（EE）的最优功率水平。

多位作者研究了各种WPCNs的能量效率。例如，文献[1]中的作者研究了多用户多输入单输出系统中基于同时无线信息与功率传输（SWIPT）的能量效率最大化问题。文献[2]中的作者研究了正交频分复用采用无线携能通信（SWIPT）的OFDMA系统。文献[3]通过联合优化下行无线能量传输（WET）功率和上行无线信息传输（WIT）功率，最大化用户能效（EE）的加权和。文献[4]研究了考虑激活子载波和用户影响的OFDMA系统中类似的发射机与接收机联合能效优化问题。文献[5]研究了移动无线传感器网络中无线携能通信（SWIPT）的能量效率，考虑了接收器的最低个人和系统数据速率要求、最低所需功率传输以及最大系统功耗。

文献[1]‐[5],以及其他相关研究在假设接收端和/或发送端已知信道状态信息（CSI）的前提下，研究了无线供电通信网络（WPCN）中的能量效率（EE）。然而，获取信道状态信息会消耗能量，从而降低系统的能量效率。因此，我们提出一种无需任何信道状态信息的学习算法，以最大化系统的能量效率。具体而言，我们考虑一个无线供电通信网络（WPCN），其中能量源向能量收集节点（EH nodes）传输能量，各节点利用收集的能量以固定速率将信息传回能量源。随后，能量源尝试解码接收到的码字，并观察哪些节点成功完成了传输。利用关于接收到的码字成功解码的有限信息，源节点学习应使用何种功率水平以最大化系统的能量效率。为此，我们将该问题建模为随机多臂老虎机问题，并设计了一种学习算法来优化能量效率。

最近在[6]和[7]中研究了无线携能通信网络（WPCN）中的学习算法。文献[6]的作者提出采用强化学习（RL）来研究设备到设备通信叠加蜂窝网络中能量效率（EE）与服务质量参数（如传输时延）之间的权衡。文献[7]的作者提出了一种基于强化学习（RL）的卸载策略，用于能量收集物联网设备为计算密集型应用选择边缘设备。这些学习算法要求设备具备信道状态信息（CSI），或知晓额外信息（如可用电池电量），而这些条件在实际中难以实现，并且会降低能量效率（EE）。本文采用多臂老虎机框架来解决能量效率（EE）问题，因为它能够为我们算法的性能提供理论保证。为此，我们提出一种基于上置信界（UCB）的学习算法，使能量源在无需任何信道状态信息（CSI）的情况下，仅根据接收到的码字是否成功解码来最大化能量效率（EE）。据我们所知，通过在无信道状态信息（CSI）知识的情况下优化功率选择策略以最大化无线携能通信网络（WPCN）的能量效率（EE），尚未被研究过。

II. 系统模型

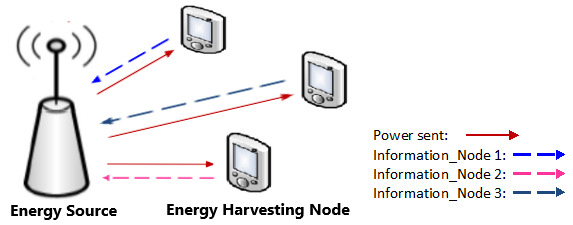
我们考虑一个系统模型，该模型由一个能量源（称为源节点）和k个能量收集（EH）无线节点（称为节点）组成。源节点和节点在k个专用信道上采用频分双工（FDD）1，每个信道占据不同的频段。具体而言，源节点在其专用信道上辐射能量，该能量被节点收集，并用于通过各自的专用信道向源节点传输信息，参见图1。需要注意的是，由于采用了频分双工（FDD），因此不会发生干扰。源节点同时也作为信息的接收器。我们假设这些专用信道为平坦衰落信道，其信道增益在每个时隙内保持恒定，并在不同时隙之间独立变化。令Gj(t) 表示在时隙t内，用于能量传输的专用信道上源节点与节点j之间的复值信道增益，其中Gj(t) ∼CN{0,σ2 Gj} ，即均值为零、方差为 σ2 Gj 的复高斯分布。令Hj(t) 表示在时隙t内，节点j通过其用于信息传输的专用信道到源节点之间的复值信道增益，其中 Hj(t) ∼ CN{0,σ2 Hj} 。我们还假设源节点接收到的信号受到方差为 σ2的复均值为零的加性白高斯噪声（AWGN）的影响。

源节点具有一组m个功率2 ，表示为 P={p1,p2,…, pm}。在每个时隙 t中，源节点可以选择 P中的任意功率进行能量传输。令P(t) ∈ P表示在时隙t中选定的功率。节点j在时隙t从功率P(t)收集的能量量，记为Ej(t)，由以下公式给出 Ej(t)= min{bmax,max(0,λP(t)|Gj(t)| 2 −pmin)}, (1) 其中，pmin 是每个节点运行所需的最小所需功率， 0 ≤λ< 1 是能量收集低效率系数，bmax 是节点电池的最大容量。我们假设节点将在时隙 t −1 内收集的全部能量用于下一个时隙 t 的信息传输。每个节点使用达到容量的码字以速率 r0 进行信息传输。在时隙 t 内，源节点从节点 j 接收到的接收速率为 Rj(t)，其表达式如下： Rj(t)= Oj(t)r0, (2) 其中 Oj(t) 是一个二进制变量，用于表示在源节点处对节点 j 的码字解码成功或失败的情况，其表达式为 O j( t)={ 1 if log2(1+ E j(t−1)|Hj(t)| 2 σ 2 )> r0 0 otherwise. (3)

1或者，我们也可以假设源节点和各节点采用时分双工（TDD）在k+1个时间槽上以避免干扰。 2所提算法同样适用于连续功率，前提是将连续功率量化为离散功率。然后，所提算法将学习接近最优连续功率的最优离散功率。

使用 Rj(t) ∀j，我们可以定义时隙t内源节点接收到的加权和速率如下 Rsum(t)= k ∑ j=1 ωjRj(t), (4) 其中 0 ≤ωj ≤ 1,∀j和 ∑k j=1ωj= 1。权重 ωj,∀j用于为用户分配不同的优先级。

III. 问题表述

接下来，我们对问题进行建模，并设计一种学习算法以最大化无线携能通信网络（WPCN）中的能量效率。

A. 问题设定

当我们增加源节点的发射功率时，节点收集的能量量仅会增加到一定程度，随后由于（1）而达到饱和。因此，进一步增加源节点的发射功率将不会提高由（4）给出的源节点接收到的加权和速率，从而导致能量浪费。因此，必然存在某个最优功率水平，能够使单位能耗所获得的加权和速率最大化。为了研究这一点，我们将能量效率定义为在n个时间槽内，源节点接收到的加权和速率与源节点发射功率之比，表示为 EE(n)= 1 n n ∑ t=1 k ∑ j=1 ωjRj(t+1) P(t) . (5) 我们的目标是确定一个最大化期望能效的固定功率水平，即我们求解以下优化问题 argmax p∈P E[EE(n) | P(t)= p, ∀ t]. (6) 在所有时间槽中采用固定功率水平的原因是源节点没有信道状态信息（CSI），因此调整每个时隙的功率等级并无益处。源节点唯一可获得的信息是来自某一节点的接收到的码字是否成功解码。基于这一有限信息，我们推导出一种策略，使源节点能够学习最优功率，以最大化由公式 (6)定义的能量效率的期望值。

B. 符号说明

我们将集合 P中的每个功率简单地以其索引表示。令 R(t) ={R1(t),R2(t)…,Rk(t)}表示在时隙t源节点处的接收速率向量，其中Rj(t)是由(2)给出的来自节点j的接收速率。注意向量 R(t) 取决于节点在前一时隙 t −1 收集的能量。在 t = 1 时，R j(1) = 0,∀j，因为节点在 t= 0 尚未收集到任何能量。设时隙 t 源节点的历史为 H(t) :={(P(1), R(1)), (P(2), R(2)) .., (P(t), R(t))}，其中 H(0) =φ。源节点的功率选择策略记为 Π={π(t)}∞ t=1，是一系列映射 π(t) : H(t −1) → P。我们的目标是找到一种策略，以最大化由公式 (6) 给出的系统的期望能效。为此，我们将该问题建模为一个多臂老虎机 (MAB) 问题，其中源节点是学习器，源节点的发射功率集合构成臂。

设Ri j(t)表示在时隙t，当源节点在时隙t −1的发射功率为P(t −1) = i时，从节点j接收到的速率。对于每个节点j和功率i，随机过程{Ri j(t)}t≥2是一个独立同分布 (i.i.d.) 随机过程，其均值记为 µij，并由 E[Rj(t+1)|P(t) = i]=µij给出。我们用i∗表示最大化期望能效的功率，并用µi∗表示相应的最优期望能效，其中 i∗= argmax i∈m k ∑ j=1 ωjµij pi and µi∗= k ∑ j=1 ωjµi∗j pi∗ . (7) 我们定义期望遗憾，用于评估所提策略与最优功率选择策略在 n 个时间槽内的平均性能差距，其表达式为 Rn=n µi∗ − ∑n t=1∑ k j=1ωj E[µIt] t j pIt， 其中 I 是在时隙 t 中选择的功率索引，pIt=P(t) 是对应的发射功率。因此，最大化平均能效等价于设计一种学习算法，通过在源节点学习最优功率水平来最小化期望遗憾。

C. 所提算法

我们使用著名的UCB方法[9]开发了一种用于最优功率选择的算法。首先，我们给出一个关于加权随机变量之和的集中界，该集中界将在算法中使用。令µˆ (s) ij表示从节点j利用来自功率i收集的能量，在源节点处获得的接收速率的s个独立同分布样本得到的经验均值，其表达式为µˆ (s)ij = 1 s∑ s t=1Ri j( t)。 由于Ri j( t) ∈{0,r0}，根据霍夫丁引理[10,公式(2.2)]，存在一个凸函数 ψ： R→ R+，使得对于所有a> 0成立。 E[exp(a(µij −Ri j))]≤ exp(ψ(a)), (8) 其中凸函数 ψ(a)= a2r02/8。 利用(8)，我们得到源节点接收到的加权和速率的集中界。

引理1. 对于任意的 s，我们有 P{ k ∑ j=1 ω j µij − k ∑ j=1 ω j µˆ (s) ij > ε}≤ exp(−sψ ∗ (ε)), 其中 ψ ∗ (ε)= supa∈R(αε −∑ k j =1 ω 2 j ψ(a))是 ψ(α)的（加权） Legendre-Fenchel变换。 证明：请参阅附录A。

引理1 表明，以概率 1−δ, ∑kj=1ωj µˆ(s) ij+(ψ ∗)−1(1s log δ1)>∑kj=1ωjµij成立 ∀i ∈m.利用该引理，我们为每个功率 i在时隙 t>m定义置信上界 UCBi(t)= k ∑ j=1 ωj µˆij(t−1)+(ψ ∗)−1( α lnt Ni(t−1)), (9) 其中 α是算法的一个输入参数，Ni(t)=∑ts=1 I{Is= i} 表示在时隙t之前功率i被选择的次数，且(ψ ∗)−1( α lnt Ni(t−1))=r0√ α lnt ∑kj=1ω2j 2Ni(t−1)。α的值越大，探索程度越高。我们提出一种基于UCB的算法，其伪代码如 算法：UCB‐EH所示，工作流程如下。UCB‐EH算法以 m种功率、k个节点和 α作为输入，其中 α是一个稍后指定的常数。在前m个时间槽中，每种功率按轮询方式依次被选择。在随后的每个时隙t中，根据公式(9)计算功率i的 UCB值。然后源节点选择使比率UCBi(t)/pi最大的功率索引i。该最大化功率索引记为It，对应的发射功率为pIt。对于所选的It，源节点观察各节点的接收速率RItj (t)，并更新所有节点的经验均值ˆµItj(t)。

UCB‐EH
1: 输入： m，k α 和 ωj，∀j
2：在前 m 个时隙中，每个发射功率各选择一次
3: 更新所有 i ∈m,j ∈k 的 ˆ µij
4： 对于 t =m +1，m +2，…，n 执行
5:对于每个功率 i ∈m，计算置信上界i(t) ← k ∑ j=1 ωj ˆ µij(t −1) +r0√ α lnt ∑k j=1ω 2 j 2Ni(t −1)
6:设置 It← arg max i 置信上界 i (t) pi 和发射功率 pI t
7:观察接收速率RIt j (t) 对于所有 j ∈k
8:更新所有 j ∈ k 的 ˆµItj(t) 估计值
9:结束循环

D. 遗憾分析

现在我们对所提出的UCB‐EH算法的性能给出理论保证。

定理1。 设∆i= µi∗ −∑ k j=1( ω j µij/pi)为功率i的次优间隙，且 ∆= min i6=i∗ ∆i。则UCB-EH在n轮后的遗憾上界为
Rn ≤6ro2 ∑ i:∆i >0 lnn∑ k j=1 ω 2 j p 2 i ∆i + ∑ i:∆i >0( π 2 3 +1)∆i, (10)
即，遗憾的阶为 O(mlnn∑ k j = 1 ω 2 j ∆)。此外，问题无关界由下式给出： Rn ≤O(√nmlnn∑ k j=1 ω 2 j) .
证明：请参见附录A。

从定理1可以看出，所提的UCB‐EH算法是渐近最优的，从而最大化期望能效。此外，所提算法的复杂度随着功率等级数m呈线性增长。

IV. 数值结果

假设为瑞利衰落，(1)式中的 |Gj(t −1)|2 和 |Hj(t)|2 分别是均值为 2σG2j 和 2σH2j 的指数分布的随机变量。方差 σG2j 和 σH2j 通过自由空间路径损耗模型计算得到，即 σx2j= 12( c 4π)2 −γ, ∈{,} fxj d j x G H，其中 c 表示光速，fxj（x ∈{G, H}）为到/来自节点j的信号的载波频率，dj为源节点与节点 j 之间的链路长度， γ为路径损耗指数。此外，(3)式中的噪声功率 σ2 由 σ2=W σ02 给出，其中 W 为带宽， σ02为每赫兹噪声功率。在我们的数值仿真中，假设带宽 W = 100 kHz，每赫兹噪声功率 σ02= −170 dBm/Hz，使得总噪声功率为 σ2= −120 dBm。我们假设载波频率 fGj= 2.4GHz 和 fHj= 2.4+(10−3 ×j) GHz，长度 d j= 10+(3×j) m， ωj= 1/k 对于 j = 1, 2,..k。此外，我们考虑路径损耗指数 γ= 2.5，能量收集低效率系数 λ= 0.5，最小功率 pmin= −60 dBm，最大电池容量 bmax ≥ −40 dBm，以及 α= 3。在我们的能量收集设置中，考虑的发射功率集合为 P={0,1,2,…,30}（单位：dBm）。

我们通过平均能效对UCB‐EH的性能进行了实证评估，并将其与无信道状态信息的基准方案进行比较。在无信道状态信息的基准方案中，源节点始终以最大功率发射以为能量收集节点充电，即以功率30 dBm发射。我们将 Oracle方案定义为基于最优策略的方案，该策略可最大化系统能效。我们的目标是使算法能够随时间学习理想方案。我们测量了算法在T= 104个时隙内的性能，且结果在 1000次重复上取平均。

在图2中，我们展示了UCB‐EH、Oracle方案以及无信道状态信息的基准方案在不同节点数k={4,8,12}和 r0= 0.1 bpcu下随时间槽数n变化所达到的能量效率。如图2所示，我们的算法实现的能量效率收敛于Oracle方案所达到的能量效率。此外，对于任意的k和任意时隙，我们的算法均显著优于无信道状态信息的基准方案。正如预期，当发射功率数量固定时，随着节点数量的增加，能量效率下降。

在图3中，我们展示了所提算法、Oracle方案以及无信道状态信息的基准方案在具有k= 5个节点时，能量效率随速率r0变化的情况。最初，随着r0,值的增加，数量节点能够以固定的源节点发射功率成功地以速率r0向源节点传输码字。因此，系统的期望能效提高并达到最大值。但当r0进一步增加时，更多节点无法成功地以速率r0向源节点传输码字，从而导致系统能效下降。如图3所示，我们的算法实现的能效比无信道状态信息的基准方案高出 52%，仅比Oracle方案低9%。此外，为了获得系统的最高能效，我们的算法和Oracle方案需要0.75 bpcu的速率，而无信道状态信息的基准方案则需要2 bpcu才能达到系统的最高能效。

在图4中，我们将我们方案的能量效率（EE）与一个拥有所有信道信道状态信息（CSI）的基准方案进行了比较，其中k= 8。为了公平比较，我们在基准方案中包含了获取信道状态信息的代价。从图4可以看出，仅当获取信道状态信息的代价非常小时，即在此示例中小于‐60 dBm时，有CSI 的基准方案才优于我们的算法；但在实际中这是不可能的，因为信道状态信息估计会消耗相当多的能量。

V. 结论

我们研究了在无线携能通信网络（WPCN）中，专用源在无信道状态信息（CSI）知识的情况下，为能量收集节点无线充电时的最优功率选择问题，以提高系统能量效率。为解决该问题，我们提出了一种基于多臂赌博机理论的在线学习方法，用于选择可最大化系统能量效率的最优发射功率。仿真结果表明，所提算法能够学习到最优功率，并显著优于基准方案。