手搓神经网络——矩阵求导

相关文章：

• 《手搓神经网络——BP反向传播》
• 《手搓神经网络——矩阵求导》
• 《手搓神经网络——Fashion MNIST训练》

前言

本文是对于《手搓神经网络——BP反向传播》一文中高级的 BP 反向传播部分的详细论述

import numpy as np
import tensorflow as tf

输入，权重与偏置

输入，权重与偏置的属性

先来聊聊输入（x）、权重（w）、偏置（b）。无需再废话的是，这三者的类型都是数组numpy.ndarray

输入（x）

输入（x）的形状为(b, n)，b表示 batch_size（批大小），n表示输入询量数据长度。下图表示 batch_size 为b的每个训练数据形状为(1, n)的训练集

输入矩阵中，x 上标表示此训练数据在一个批大小中的位置，x 下标表示第b个训练数据的第n个参数

权重（w）

权重（w）的形状为(n, m)，n表示输入数据数量，m表示该层输出数据数量（即该层的神经元数量）

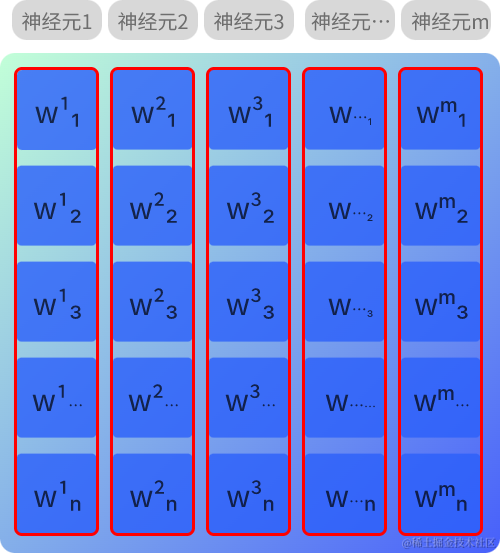
在全连接层中，每层的各个神经元相互交织连接。权重矩阵中，w 上标表示的是该层的第 m 个神经元，w 下标表示的是该层第 m 个神经元与第 n 个输入的联系

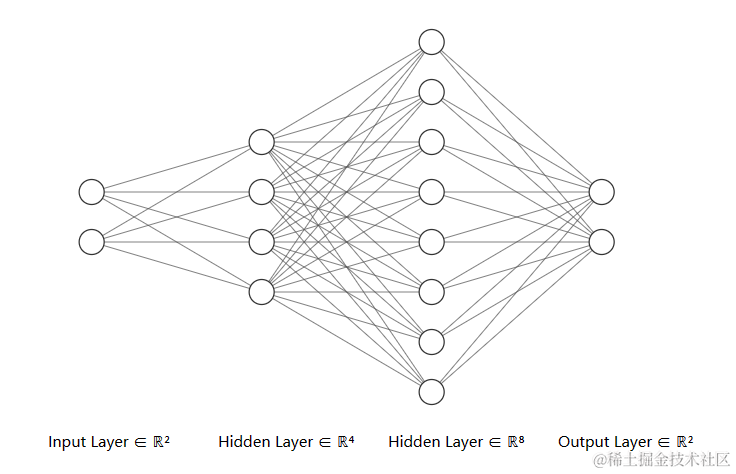
偏置（b）

偏置（b）的形状为(1, m)，m表示该层输出数据数量（即该层的神经元数量），图中的 b1、b2、b3…分别表示神经元1、神经元2、神经元3…的偏置

输入，权重与偏置的计算

关于计算不多赘述，就是 $x@w+b$ ，在本文中@表示矩阵叉乘，用numpy表示即为x@w+b或者np.dot(x, w)+b，在将其计算结果带入激活函数，得到的即为神经网络层的输出，笔者认为前向运算的本质就是矩阵计算，反向传播的本质就是矩阵求导

矩阵求导

在输出层计算部分之前，单独论述下矩阵求导。主要论述x@w+b 对 w 求导与激活函数对 x@w+b 的求导

x@w+b 对 w 求导

下面有一个x@w+b表达式，嚯！看着挺复杂的，实则是笔者这里写的详细了些，与其说复杂倒不如是繁琐

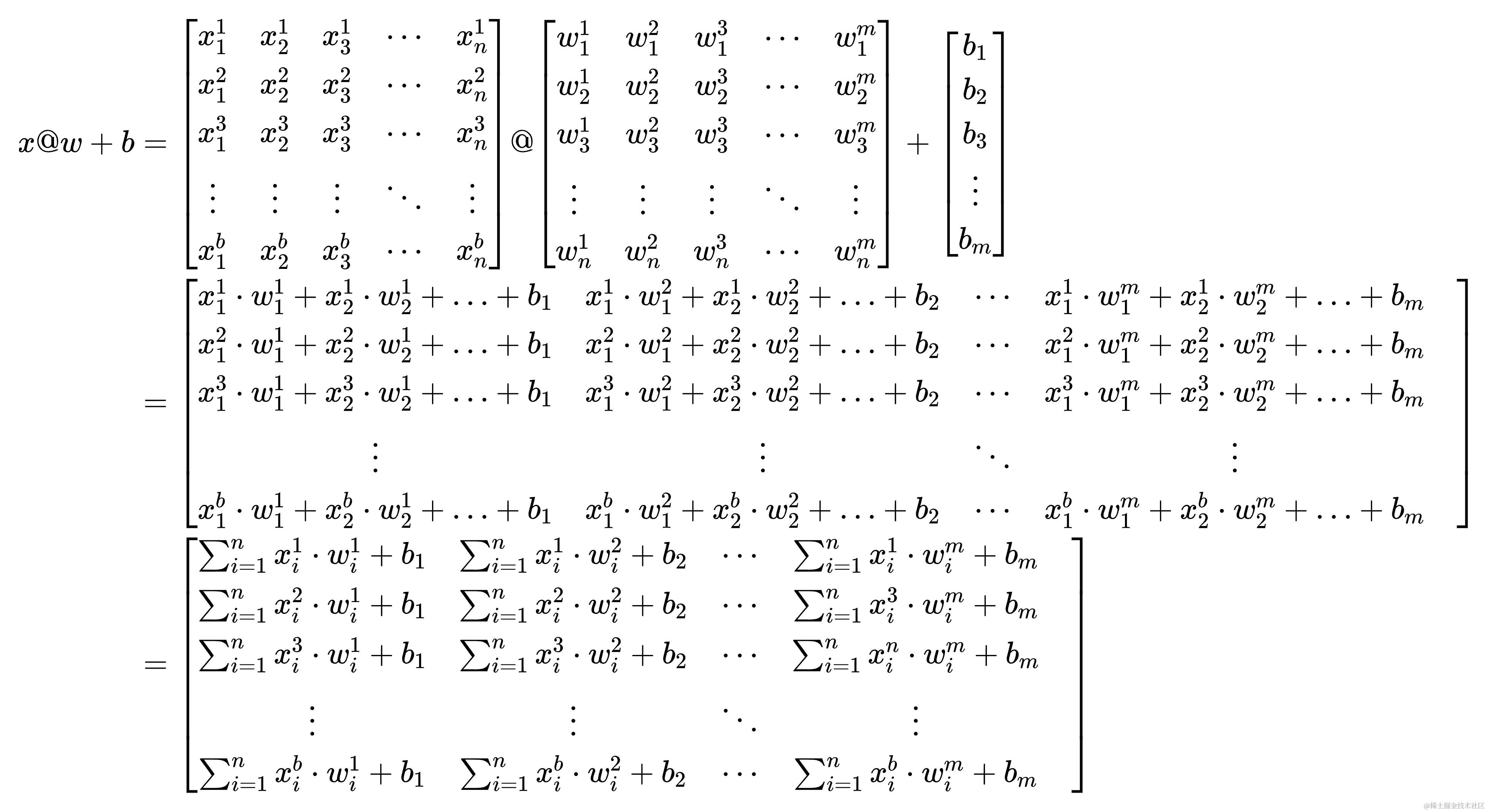
接下来，加一点魔法🪄，让x@w+b叉乘✖一个形状为(m, 1)的全一矩阵（矩阵里全是一①Ⅰ壹），m与权重（w）中m的含义相同。将这个矩阵记作 ${\alpha }_1$。哈哈，好像高中写数学题，要化简时经常要用到神奇的1

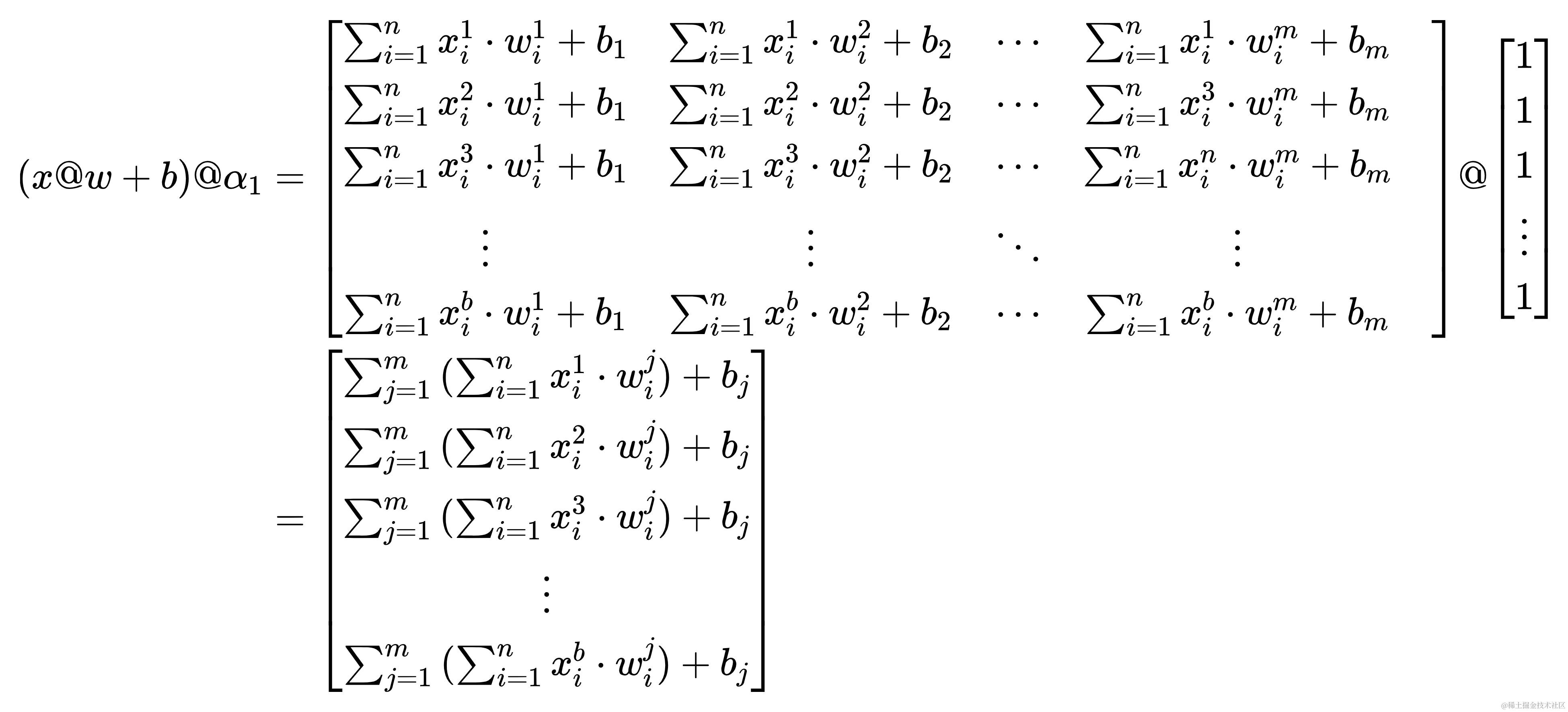
这样子，得出的结果看着就简洁多了。然后如法炮制，只不过是让一个形状为(1, b)的全一矩阵叉乘✖ $(x@w+b)@{\alpha }_1$，将这个矩阵记作 ${\alpha }_2$。哈哈哈，汗流浃背了吧，兄弟😅，你八成是看傻了，我两成是写傻了

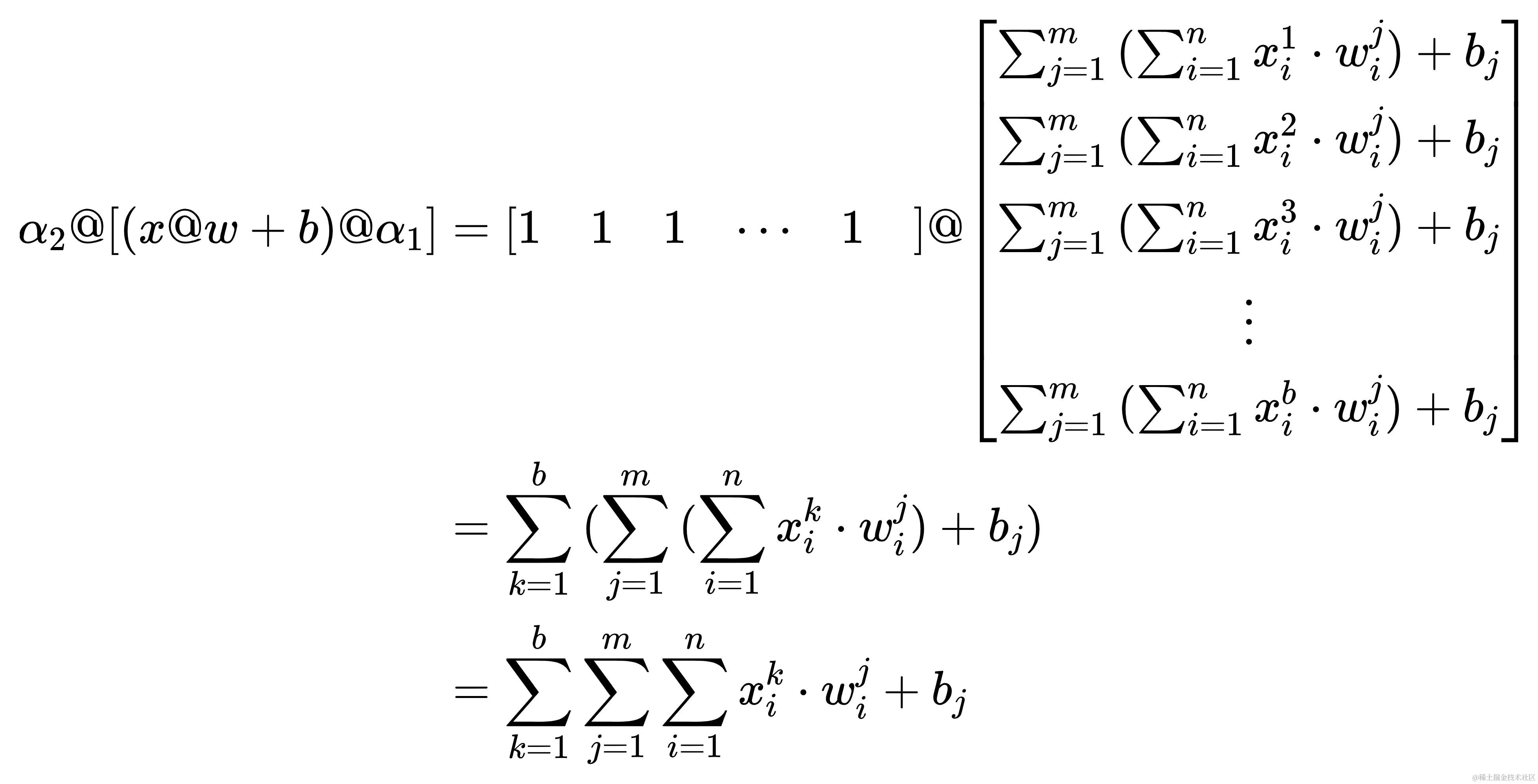
经过一坨又一坨的变换，最终以一个标量的表达式来表示最初的x@w+b（${\alpha }_1$ 与 ${\alpha }_2$ 是为了化简成上方的形式而存在的，之所以要化简成上方形式是为了使表达式更简洁，也是为了便于对w求导）

计算 ${\sum }_{k=1}^b{\sum }_{j=1}^m{\sum }_{i=1}^n{x}_i^k\cdot w_i^j+b_j$ 对 $w_i^j$ 的导数

$$\frac{\mathrm{dy}}{\mathrm{d}{w}_i^j}=\frac{\mathrm{d}}{\mathrm{d}{w}_i^j}\sum _{k=1}^b\sum _{j=1}^m\sum _{i=1}^n{x}_i^k\cdot w_i^j+b_j=\sum _{k=1}^b{x}_i^k$$

自此长篇大论得出的结论，x@w+b对w的导数表示成矩阵形式为

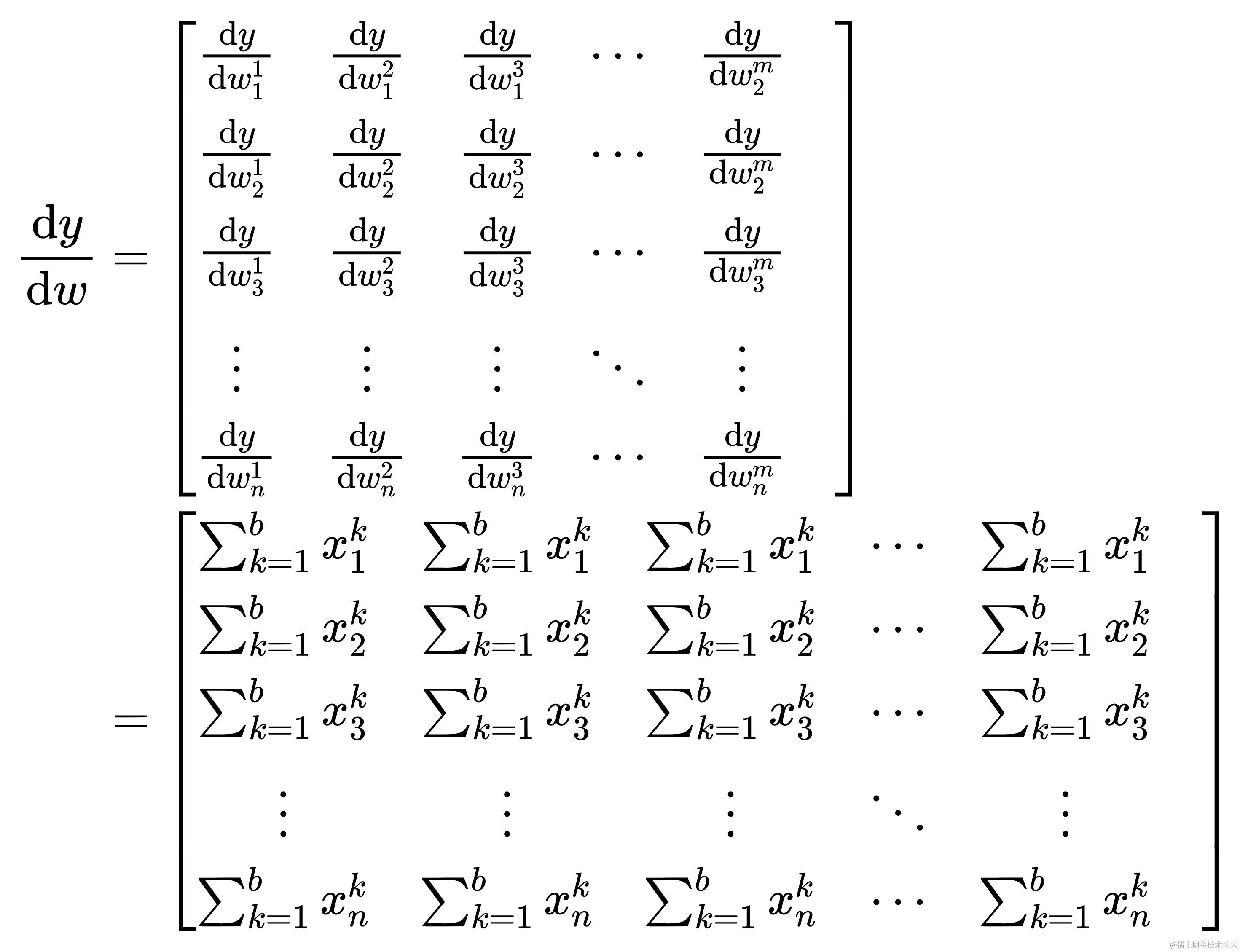
可以看得出x@w+b 对 w 的导数为 x 矩阵转置的行之和，且重复扩展成原形状（不是哥，你要问我怎么看出来是转置的？熟读并抄写10遍上文，还不晓得？熟读全文并背诵）

上面的话似乎有些难以理解，来点魔法。将形状为(b, m)全一矩阵记作 ${\alpha }_3$，用数学的语言表达如下

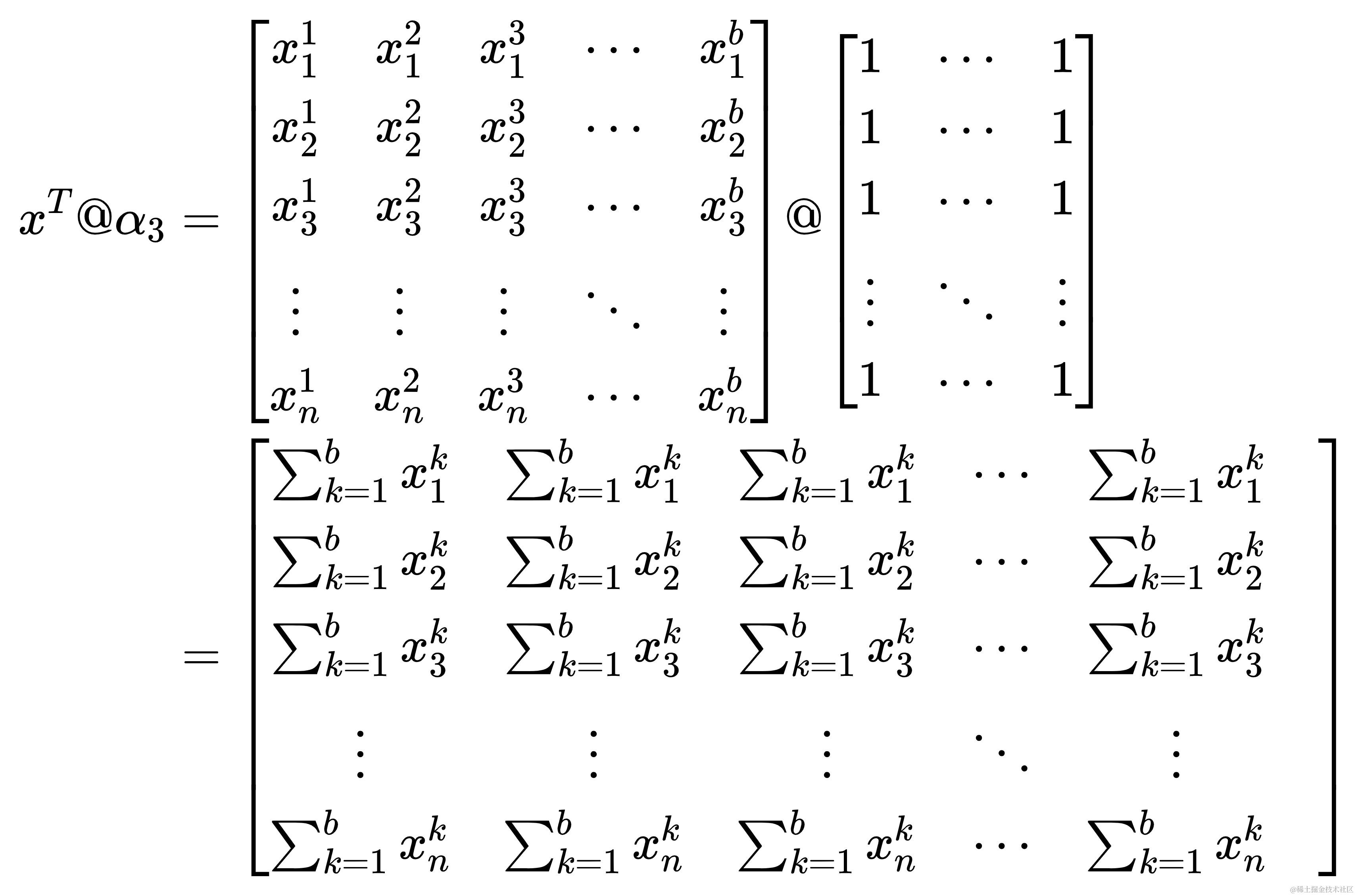
${\alpha }_3$ 的应用实现了两个功能，即上文所述的求行之和与重复扩展

• 求行之和：在矩阵叉乘中，可视为 $x^T$ 的行与 ${\alpha }_3$ 的列的点乘求和
  • 具体来说，$x^T@{\alpha }_3$ 的结果是一个列向量，其第 i 个元素是 x T x^{T}