Python将文件大小以概率分布图的方式进行统计

《深度学习-如何提高数据集质量》

项目背景

我是在做计算机项目的时候会遇到这种问题，当使用爬虫爬取大量图片后，图片大小参差不齐，有些图片明显是不可使用的，比如很小的图片就很可疑（在机器学习的时候可能无法使用），而你又不知道小图片在你的存贮空间中的占比，这就需要Python的概率分布图来标识了。

代码功能

1.用户手动输入图片的路径。这个路径是已经整理过的了，全部都是图片。
2.将小于512K的图片筛选出来。
3.显示小于512K的图片概率分布。

代码内容

import matplotlib.pyplot as plt
import os


def getFileSizeList(path):
    sizeList = []
    for filename in os.listdir(path):
        fullName = os.path.join(path, filename)
        size = os.path.getsize(fullName)
        #只把小于512K的图片放入队列
        if size // 1024 < 512:
            sizeList.append(size)
    return sizeList

x = getFileSizeList('/home/king/PycharmProjects/nsfw_data_scrapper/raw_data/sexy')

fig,(ax0,ax1) = plt.subplots(nrows=2,figsize=(9,6))

#第二个参数是柱子宽一些还是窄一些，越大越窄越密,数据多的时候将这个数值写大一些。
ax0.hist(x,100,normed=1,histtype='bar',facecolor='yellowgreen',alpha=0.75)
##pdf概率分布图，一万个数落在某个区间内的数有多少个
ax0.set_title('pdf')

ax1.hist(x,100,normed=1,histtype='bar',facecolor='pink',alpha=0.75,cumulative=True,rwidth=0.8)
#cdf累计概率函数，cumulative累计。比如需要统计小于5的数的概率
ax1.set_title("cdf")

fig.subplots_adjust(hspace=0.4)
plt.show()

概率分布效果

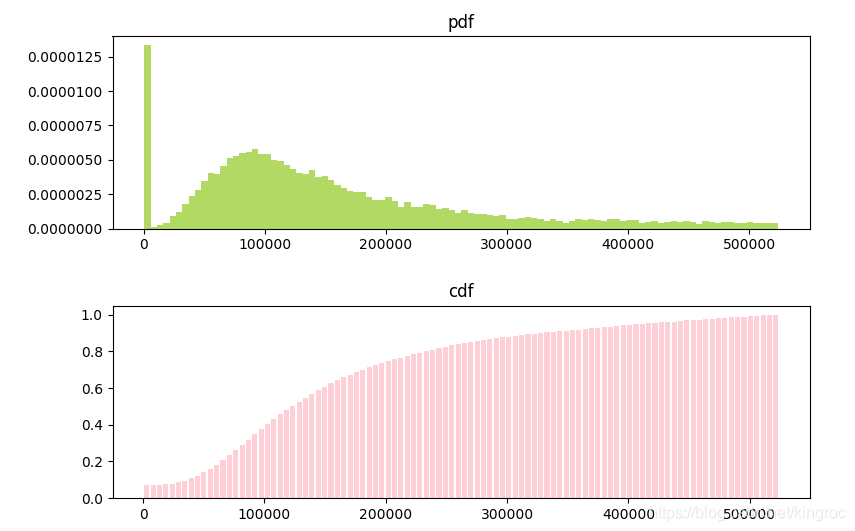
很明显小于512K的图片是一个高高的柱子，占比最大。在这里面应该能找到不少可疑的图片。