蓝桥备赛（八）- 位运算和操作符属性（上）-优快云博客

本文链接：https://blog.youkuaiyun.com/khjjjgd/article/details/145962917

一、操作符的分类

上述的操作符，已经介绍过 算术操作符、赋值操作符、逻辑操作符、条件操作符和部分的单目操作符，今天继续介绍⼀组和位运算相关的操作符（ 与二进制有关） 。首先先铺垫⼀下⼆进制的和进制转换的知识。

二、二进制和进制转化

我们经常可以听到 2进制、8进制、10进制、16进制的讲法，那么它们是什么意思呢？

----> 无论是 2进制、8进制、10进制、16进制 , 它们表示的都是数值，只是数值的不同表示方法罢了

介绍一下二进制：

生活中经常用到的是十进制：

1）10进制满10进1

2）10进制的数字是由0 ~ 9 的数字组成的

其实二进制的数字也是一样的：

1）2进制满2进1

2）2进制的数字是由0 ~ 1 的数字组成的

2.1 二进制转十进制

10 进制的 123 表示的值是⼀百二十三，为什么？

其实 10 进制的每⼀位是有权重的， 10 进制的数字从右向左是个位、十位、百位....，分别每⼀位的权重是 10^0 , 10^1 , 10^2 ...

2 进制和 10 进制是类似的，只不过 2 进制的每一位的权重，从右向左是: 2^0 , 2^1 , 2^2 ...

8进制数转10进制数，方法类似，只是权重是 8^ 0 开始，然后依次是： 8^0, 8^1...

16进制数转10进制数，方法类似，只是权重是 16^0 开始，然后依次是： 16^0 , 16^1 , 16^2

...

2.2 十进制转二进制

2.3 二进制转八进制

8 进制的数字每⼀位是 0~7 中的数字， 0~7 中的数字，各自写成 2 进制， 最多有 3 个 2 进制位就足够了！

----> 比如 7 的二进制是 111 ，所以在 2 进制转 8 进制数的时候，从 2 进制序列中右边低位

开始向左每 3 个 2 进制位会换算一个 8 进制位，剩余不够 3 个 2 进制位的直接换算。

如： 2 进制的 01101011 ，换成 8 进制： 0153 ， 0 开头的数字，会被当做 8 进制。

同样的， 8进制数转换2进制数是相关的过程，每一个8进制位转换成3个2进制位就可以了。

2.4 二进制转十六进制

16 进制的数字每⼀位是 0~9 , a~f 的， 0~9 , a~f 的数字，各自写成 2 进制， 最多有 4 个 2 进制位就足够了 ，比如 f 的⼆进制是 1111

----> 所以在 2 进制转 16 进制数的时候，从 2 进制序列中右边低位开始向左每 4 个 2 进制位会换算⼀个 16 进制位，剩余不够 4 个⼆进制位的直接换算。

如： 2 进制的 01101011 ，换成 16 进制： 0x6b ， 16 进制表示的时候前⾯加 0x

16进制数转换2进制数是相关的过程，每⼀个16进制位转换成4个2进制位就行

2.5 原码、反码、补码

在计算机内部， 数值是以 2进制的形式来表示和存储 。

后面咱们讲到的位运算的操作符，就是针对 整数的二进制 来进行运算的 :

1) 位移运算符 : >> <<

2) 位运算符： & | ^

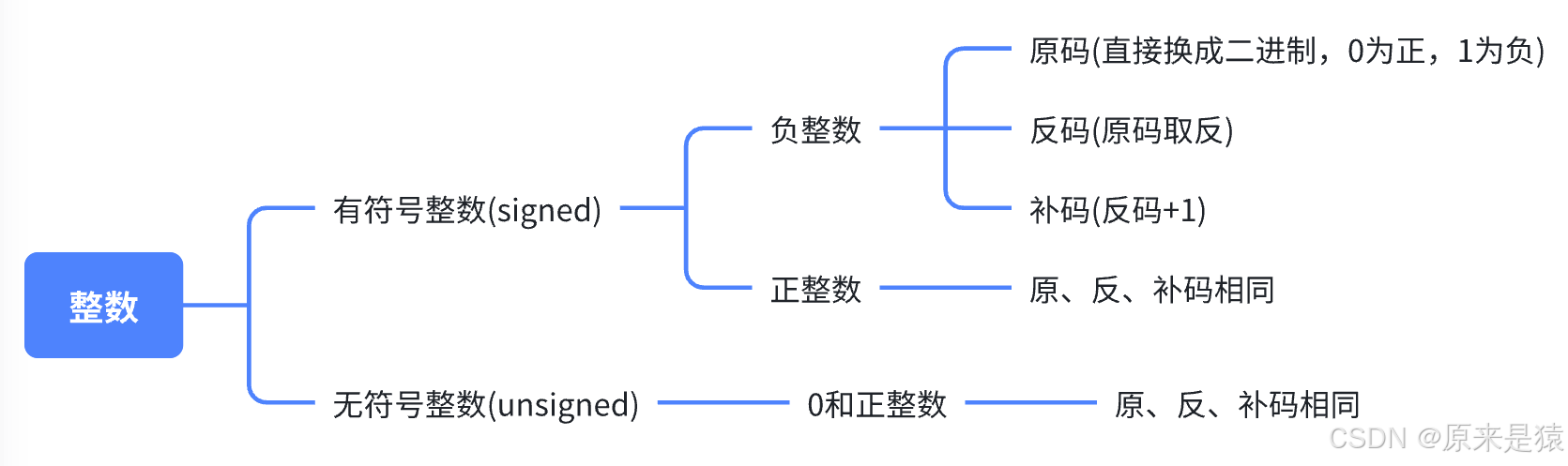
整数的二进制的表示方式有三种， 即原码、反码、补码 ；整数分为有符号整数(signed) 和无符号整数(unsigned) 。

有符号整数的原码、反码和补码的二进制表示中均由 符号位和数值位两部分组成 ， 2进制序列中，最高位1位是被当做符号位，剩余的都是数值位，符号位都是用 0 表示正，用1表示负。

1）正整数的原码、反码、补码都相同

2）负整数的原码、反码、补码各不相同，需要计算

1）原码：直接将数值按照正负数的形式翻译成二进制得到的就是原码。

2）反码：将原码的 符号位不变 ，其他 位依次按位 取反 就可以得到反码。

3）补码：反码 +1 就得到补码。

4）由补码得到原码也是可以使用：取反， +1 的操作。

下面举个例子：

无符号整数的三种二进制的表示相同，没有符号位，每一位都是数值

整数在内存中是以补码的形式存储的，整数在参与位运算的时候，也都是使用内存中的补码进行计算的，计算的产生结果也是补码，需要转化成原码才是真实值。

也就是说，计算机计算用补码，得出来的结果也是补码，但是我们屏幕上看到的是转化后的原码

问：为什么整数在内存中存放的是补码？

在计算机系统中，整数的数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值为统一处理 ；同时，加法和减法也可以统一处理(CPU只有加法器) ；此外，补码与原码的互相转化，其运算过程是相同的，不需要额外的硬件电路。

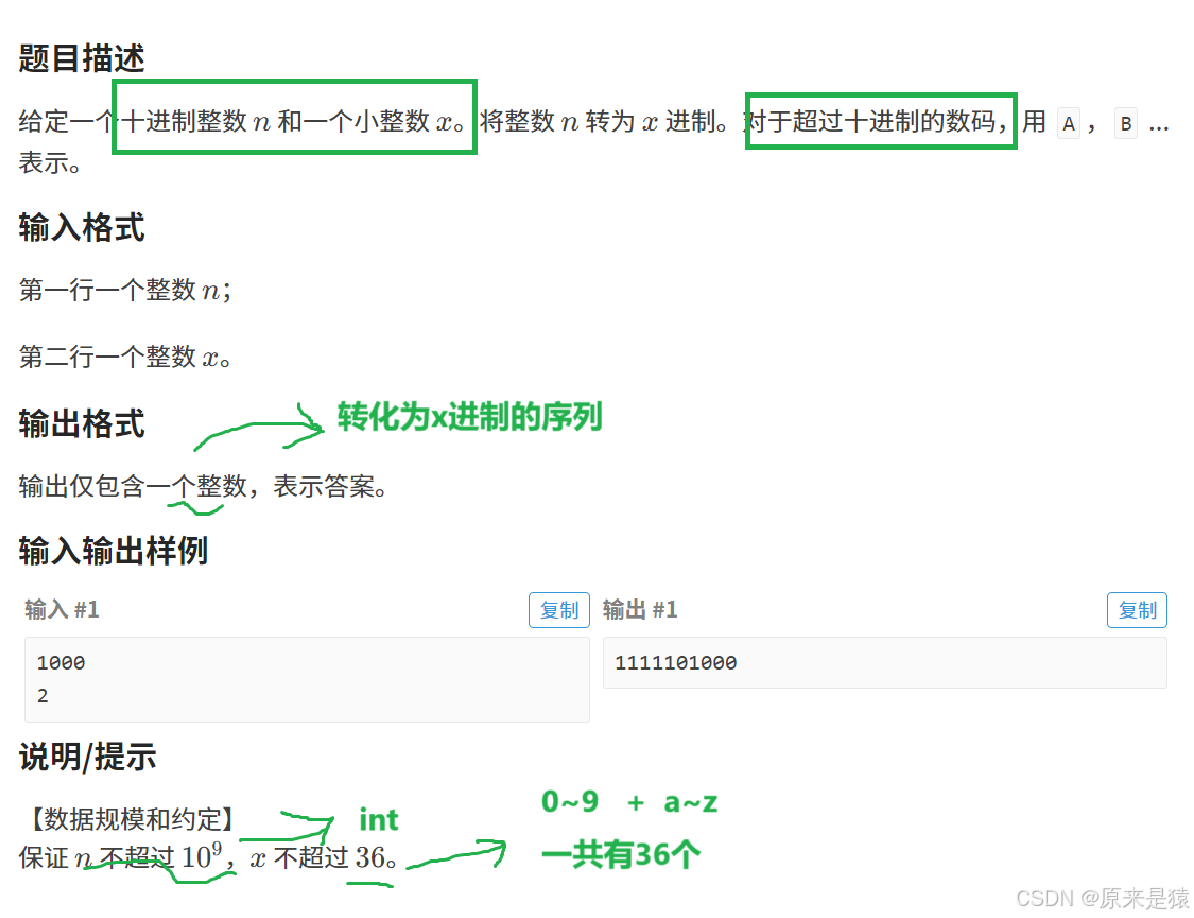
练习一：10进制转进制

B3619 10 进制转 x 进制 - 洛谷

#include <iostream>
#include <cstdio>
using namespace std;

string s = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ";
void n_to_x(int n,int x)
{
	if(n >= x)
		n_to_x(n / x , x);
	cout << s[n % x];
}
int main()
{
	int n,x;
	cin >> n >> x;
	n_to_x(n,x);
	return 0;
}

练习二：x进制转10进制

B3620 x 进制转 10 进制 - 洛谷

#include <iostream>
#include <cstdio>
#include <cmath>
#include <string>
using namespace std;

int main()
{
	int x;
	string s;
	int ret = 0;
	int i = 0;
	cin >> x >> s;
	int n = s.size();
	while(n--)
	{
		if(s[n] <= '9')
			ret += (s[n] - '0') * pow(x,i);
		else
			ret += (s[n] + 10 - 'A' ) * pow(x,i);
		i++;
	}
	cout << ret << endl;
	return 0;
}

方法二：借助stoi 函数（包含头文件，可以把字符串转换为对应进制的整数）

蓝桥备赛（五）- string(下)-优快云博客

#include <iostream>
#include <cstdio>
#include <cmath>
#include <string>
using namespace std;

int main()
{
	int x;
	string s;
	cin >> x >> s;
	int ret = 0;
	ret = stoi(s,NULL,x);
	cout << ret << endl;
	return 0;
}

练习三：进制转换

P1143 进制转换 - 洛谷

#include <iostream>
#include <cstdio>
#include <cmath>
#include <string>
using namespace std;

string str = "0123456789ABCDEF";
void n_to_m(int num, int m)
{
	if(num >= m)
		n_to_m(num / m , m);
	cout << str[num % m];
}
int main()
{
	int n;
	string s;
	int m;
	cin >> n >> s >> m;
	int num = stoi(s,NULL,n);
	n_to_m(num,m);
	return 0;
}

三、位运算操作符

<< //左移操作符

>> //右移操作符

& //按位与操作符

| //按位或操作符

^ //按位异或操作符

~ //按位取反操作符

这些位运算的操作符，只适用与整数，不能应用于其他数据类型。

注意：char 类型的字符再内存中是以ASCII码值存储的，所以也可以使用位运算的操作符。float 是肯定不行的。

3.1 左移操作符

移动规则：左丢弃，右补0

左移操作符是双目操作符，形式如下：

int num = 10;

num << i ;

// 意思是：将num 用二进制表示，左移 i 位

移位操作符，移动的是存储在内存中补码的二进制序列

举例：正整数 10

#include <iostream>
#include <cstdio>
using namespace std;

int main()
{
	int num = 10;
	int n = num << 1;
	cout << "num = " << num << endl;
	cout << "n = " << n << endl;
	return 0;
}

我们发现， 位移并不会改变num 的原来的值，这不难理解 ，

a = 10;

b = a + 1 ;

所以有 a = 10 , b = 11 ; 并不会改变a 的值，

如果要改变num 的值，可以使用 <<=

对于正整数和无符号整数，左移一位有乘以2的效果

对于负数来说，会比较麻烦一些，需要求出补码，然后左移，最后求出原码。

3.2 右移操作符

右移操作符是双目操作符，形式如下：

int num = 10;

num >> i ;

// 意思是：将num 用二进制表示，右移 i 位

移位操作符，移动的是存储在内存中补码的二进制序列

右移运算分两种：逻辑右移和算术右移 ，具体采用那种方式取决于编译器，大多数编译器采用的是逻辑右移。

1）逻辑右移：左边用0填充，右边丢弃

2）算术右移：左边用原数值的符号位填充，右边丢弃。

#include <iostream>
#include <cstdio>
using namespace std;

int main()
{
	int num = -1;
	int n = num >> 1;
	cout << "num = " << num << endl;
	cout << "n = " << n << endl;
	return 0;
}

注意：对于移位运算符，不要移动负数位，这是标准未定义的

比如：int num = 10;

num << -1; //error

3.3 按位与移操作符

按位与操作符是双目操作符，形式如下：

a & b ; //a和b的按位与运算

规则：对两个数的对应二进制位进行与运算，只有对应的两个二进制位都为1时，结果才为1（全1为1）

代码演示：

int main()
{
	int a = -5;
	int b = 7;
	int c = a & b;
	cout << c << endl;
	return 0;
}

3.4 按位或移操作符

按位或操作符是双目操作符，形式如下：

a | b ; //a和b的按位或运算

规则：对两个数的对应二进制位进行或运算，对应的两个二进制位只要为1时，结果就为1（全0为0）

代码演示：

#include <iostream>
#include <cstdio>
using namespace std;

int main()
{
	int a = -5;
	int b = 7;
	int c = a | b;
	cout << c << endl;
	return 0;
}

3.5 按位异或移操作符

按位异或操作符是双目操作符，形式如下：

a ^ b ; //a和b的按位异或运算

规则：对两个数的对应二进制位进行异或运算，对应的两个二进制位相同则为0，相异为1（相同为0，相异为1）

代码演示：

#include <iostream>
#include <cstdio>
using namespace std;

int main()
{
	int a = -5;
	int b = 7;
	int c = a ^ b;
	cout << c << endl;
	return 0;
}

3.6 按位取反移操作符

按位取反操作符是双目操作符，形式如下：

~a ; //a的按位取反运算

规则：对两个数的对应二进制位进行取反运算，则0 变1 ， 1 变 0（取反）

代码演示：

#include <iostream>
#include <cstdio>
using namespace std;

int main()
{
	int a = -5;
	int b = ~a;
	cout << b << endl;
	return 0;
}