Capacitated Facility Location Problem-蚁群算法-遗传算法-js实现

问题描述：

• Suppose there are n facilities and m customers. We wish
  to choose:
  • which of the n facilities to open
  • the assignment of customers to facilities
• The objective is to minimize the sum of the opening cost
  and the assignment cost.
• The total demand assigned to a facility must not exceed
  its capacity.

report

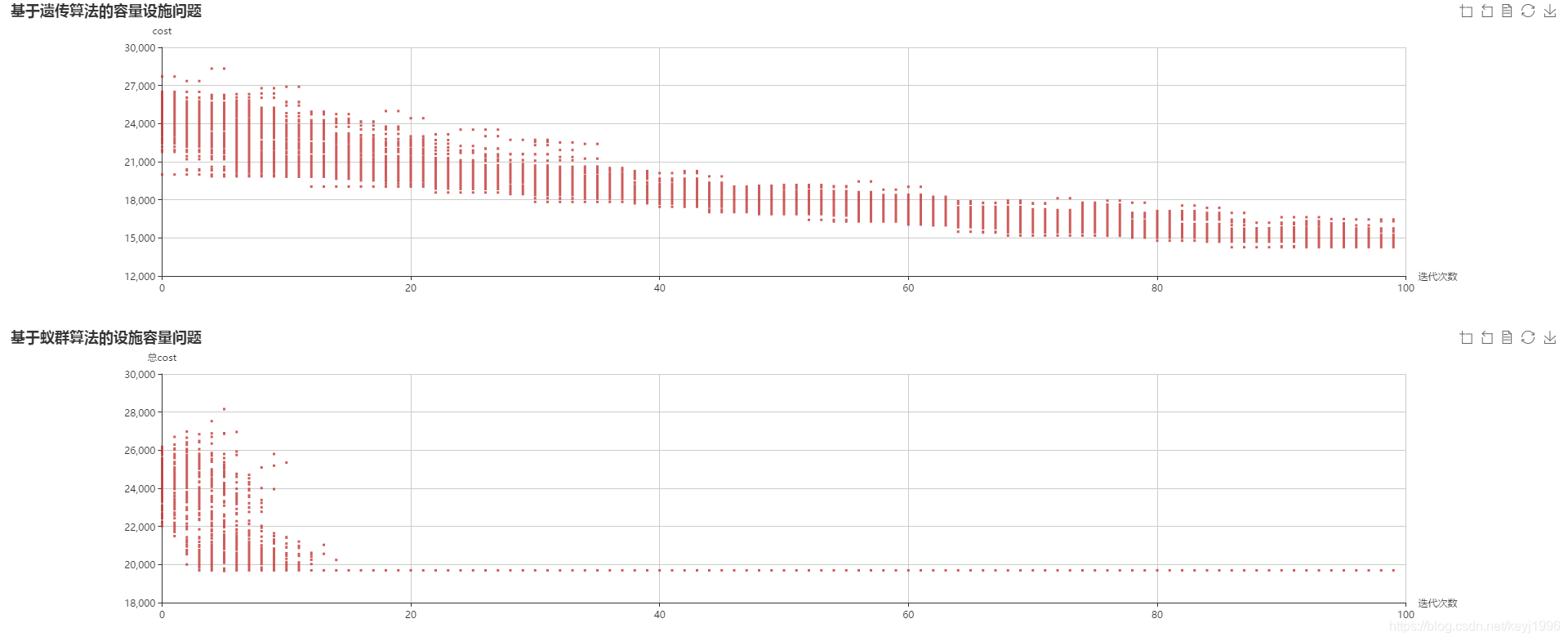
在本次实践中，我分别采用了蚁群算法和遗传算法来对问题进行求解。

蚁群算法是一种用来寻找优化路径的概率型算法。它由Marco Dorigo于1992年在他的博士论文中提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。

遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法

代码

// 遗传算法

/** 染色体数量 */
let chromosomeNum = 100

/** 适应度矩阵(下标：染色体编号、值：该染色体的适应度) */
let adaptability = []
/** 自然选择的概率矩阵(下标：染色体编号、值：该染色体被选择的概率) */
let selectionProbability = []

/** 染色体复制的比例(每代中保留适应度较高的染色体直接成为下一代) */
let cp = 0.2
/** 参与交叉变异的染色体数量 */
let crossoverMutationNum = chromosomeNum * (1-cp)

/** 任务处理时间结果集([迭代次数][染色体编号]) */
// let resultData = []

/**
 * 初始化遗传算法
 * 初始化 顾客集合、处理设施集合
 * @param _facilities 设施参数
 * @param _demands 顾客的要求
 * @param _assignmentCost 顾客到指定设施的cost
 */

function startGa(_facilities, _demands, _assignmentCost) {
   
   
    facilities = _facilities.reduce((all, now) => all.concat(Number(now.split(' ').filter(n=>n)[0])), [])

    openCost = _facilities.reduce((all, now) => all.concat(Number(now.split(' ').filter(n=>n)[1])), [])

    customers= _demands.reduce((all, now) => all.concat(now.split(' ').filter(n =>n).map(n =>Number(n))), [])

    let tp =[]
    /* _assignmentCost.forEach(_assign => {
        assignment.push(_assign.split(' ').filter(n => n).map(n => Number(n)))
    }) */
    
    let nums = _assignmentCost.reduce((all, now) => all.concat(now.split(' ').filter(n =>n).map(n =>Number(n))), [])
    while (nums.length) {
   
   
        console.log(nums)
        tp.push(nums.splice(0, customerNum))
    }
    debugger
    for (let i = 0; i < customerNum; i++) {
   
   
        for (let j = 0; j < facilityNum; j++) {
   
   
            if (!assignment[i]) {
   
   
                assignment[i] = []
            }
            assignment[i][j] = tp[j][i]
        }
    }


}

// startGa(lines.slice(1, facilityNum+1), lines.slice(facilityNum+1, facilityNum+1+customerNum/10), lines.slice(facilityNum+1+customerNum/10))

/**
 * 遗传算法
 */
function ga() {
   
   
    // 迭代搜索
    gaSearch(iteratorNum, chromosomeNum)
}

/**
 * 计算 染色体适应度
 * @param chromosomeMatrix
 */
function calAdaptability(chromosomeMatrix) {
   
   
    // 计算每条染色体的cost
    adaptability = calCost_oneIt(chromosomeMatrix).map(n => 1/n)
}

/**
 * 计算自然选择概率
 * @param adaptability
 */
function calSelectionProbability(adaptability) {
   
   
    selectionProbability = []

    // 计算适应度总和
    let sumAdaptability = 0
    for (let i=0; i<chromosomeNum; i++) {
   
   
        sumAdaptability += adaptability[i]
    }

    // 计算每条染色体的选择概率
    for (let i=0; i<chromosomeNum; i++) {
   
   
        selectionProbability.push(adaptability[i] / sumAdaptability)
    }
}

/**
 * 迭代搜索
 * @param iteratorNum 迭代次数
 * @param chromosomeNum 染色体数量
 */
function gaSearch(iteratorNum, chromosomeNum) {
   
   
    // 初始化第一代染色体
    let chromosomeMatrix = createGeneration()

    // 迭代繁衍
    for (let itIndex=1; itIndex<iteratorNum; itIndex++) {
   
   
        // 计算上一代各条染色体的适应度
        calAdaptability(chromosomeMatrix)

        // 计算自然选择概率
        calSelectionProbability(adaptability)

        // 生成新一代染色体
        chromosomeMatrix = createGeneration(chromosomeMatrix)
    }
}


/**
 * 交叉生成{crossoverMutationNum}条染色体
 * @param chromosomeMatrix 上一代染色体矩阵
 */
function cross(chromosomeMatrix) {
   
   
    let newChromosomeMatrix = []
    for (let chromosomeIndex=0; chromosomeIndex<crossoverMutationNum; chromosomeIndex++) {
   
   

        // 采用轮盘赌选择父母染色体
        let chromosomeDad = chromosomeMatrix[RWS(selectionProbability)].slice(0)

        let chromosomeMom = chromosomeMatrix[RWS(selectionProbability)].slice(0)
        // 交叉
        let crossIndex = random(0, customerNum-1)
        chromosomeDad.splice(crossIndex)
        chromosomeDad = chromosomeDad.concat(chromosomeMom.slice(crossIndex))

        while (!checkIfLegal(chromosomeDad)) {
   
   
            console.log('cross')
            chromosomeDad = chromosomeMatrix[RWS(selectionProbability)].slice(0)

            chromosomeMom = chromosomeMatrix[RWS(selectionProbability)].slice(0)

            crossIndex = random(0, customerNum-1)
            chromosomeDad.splice(crossIndex)
            chromosomeDad = chromosomeDad.concat(chromosomeMom.slice(crossIndex))
        }
        newChromosomeMatrix.push(chromosomeDad)
    }
    return newChromosomeMatrix
}

/*
 *看一条染色体是否是可行解
 *@param chromosome 染色体
 */

function checkIfLegal(chromosome) {
   
   

    let usedCapacity= {
   
   }
    for (let i = 0; i < chromosome.length