LeetCode 10. Regular Expression Matching

题目

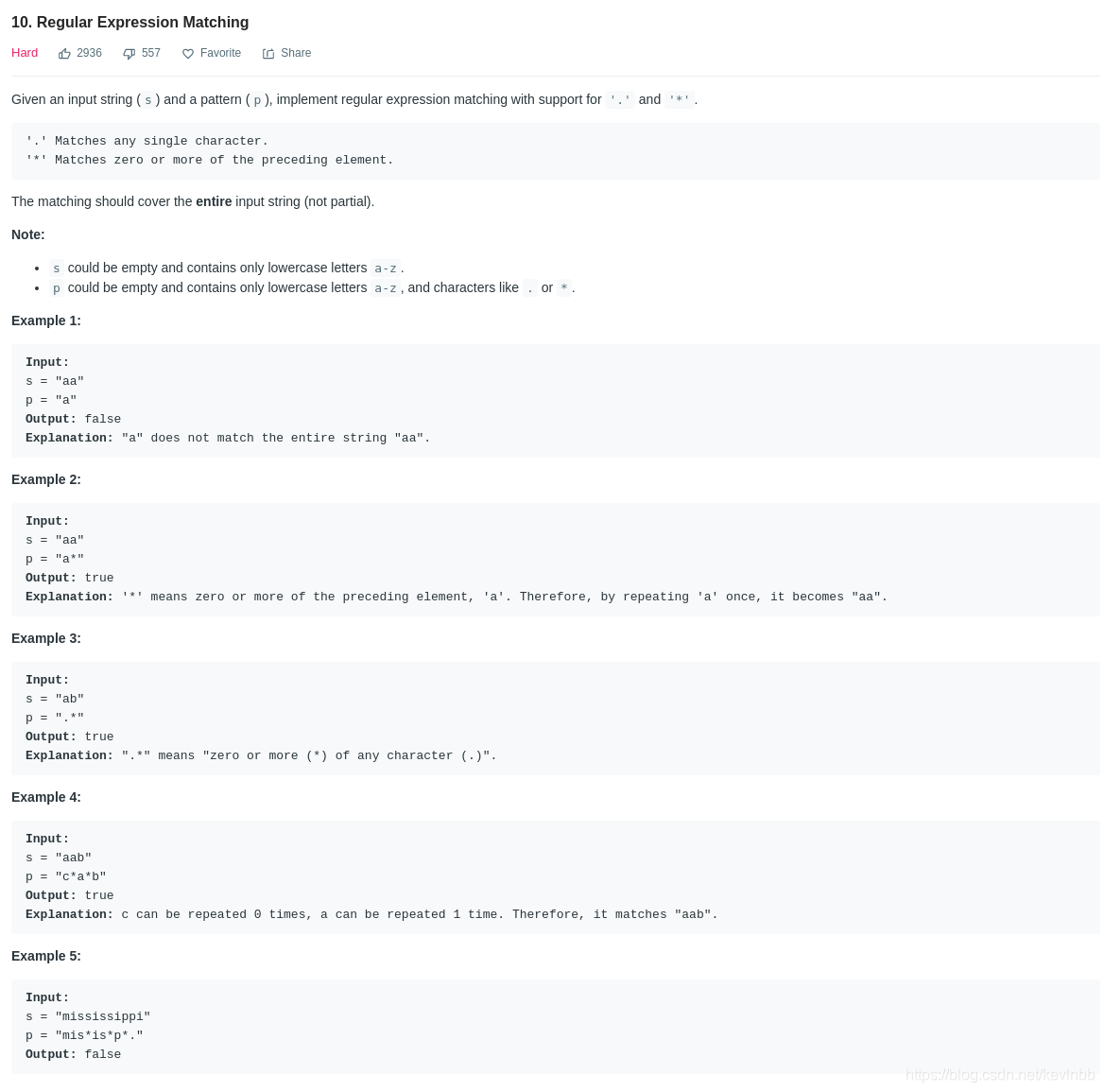
分析

一道开始去想确实hard的题目，原因就在于*这个情况把题目给复杂化了，没关系，一步一步，庖丁解牛。

这题主流的两种做法就是递归和dp，其实这题递归来写我感觉并不比dp轻松，原因都是需要考虑比较多的情况。这里先来记录dp的做法，等以后有机会再补上递归写法。
dp无非就是考虑边界和一般情况，这种双字符串比较的dp一般都是开二维数组dp[][]。为了方便考虑到空串的情况，dp[i][j]的含义定义为串s中长度为i的前缀和串p中长度为j的前缀的匹配情况。
先看边界，i和j都是0的时候，也就是s串和p串都是空串，按理说是匹配的，所以有

dp[0][0] = true

。接下来就是考虑dp矩阵的第一条长和第一条宽。
第一条长也就是i=0的情况，即s串为空，那这种情况如果需要p跟s匹配，只可能是p[j-1]是*，因为s是空，p要想匹配，那p也得表示成空，但是p是有长度的（i == 0 j >= 1），所以只可能通过*使之变空。具体的式子是

dp[0][j] = dp[0][j - 2] && ( p[j - 1] == '*')

注意是j-2，这是因为在p下标为j-1的*只能让前一个字符出现0次，也就意味着比较方式转移成了j - 1的前前字符跟i-1进行比较。j - 1的前前是j - 3，即dp[0][j - 2]

ps:可能有人会说到这个式子中有j-2，那会不会出现下标小于0的情况呢？
其实是不会的，具体的处理方法可以让j从2开始遍历，为什么可以从长度2开始遍历呢，很简单，因为当s是空串，p长度为1的时候，是肯定不可能匹配的(p的第一个字符不可能是※因为没有意义)。注意这一点就把边界处理好了。

下面考虑一般情况，即s和p都不为空的时候。
首先最简单的第一种情况，当对应位置相同，或者是p是.，那这两个位置的dp情况就可以退到前一个位置去比较了，这个相信所有人都不难理解，即

dp[i][j] = dp[i - 1][j - 1]     (if s[i - 1] == p[j - 1] || p[j - 1] == '.')

第二种情况，也就是让这题变成hard的，即p和q对应位置不同，该怎么变化。因为加入了*，让这题的变化就显得复杂起来。
首先我们需要清楚，当这两个位置不相等，我们需要考虑的只可能是p位置为的情况（因为只有才能发生字符串变化），对于一般的不相等，肯定就是false了，默认就是false，所以不需要考虑。
那对于这个p是※的情况，需要考虑哪些呢？※的改变方法其实就三种情况，一是让前面的元素出现0次，二是让前面的元素出现一次，三是让前面的元素出现多次。那我们就需要考虑对号入座的情况。比方说当前位置p是*，和s不匹配了，那么考虑前一个位置和s匹不匹配。
如果匹配，那※可以使※前一个位置出现1次，由于我们无法知道s后面是什么情况，我们也可以让※前面一个位置出现多次，同理不清楚s前面是什么情况，所以也可以让前面这个位置出现0次，这三种只要一种满足了，那这个位置都可以匹配，所以是或的关系。

dp[i][j] = dp[i][j - 1] (前面出现一次) || dp[i][j] = dp[i][j - 2] （前面出现0次） 
|| dp[i - 1][j] （前面出现多次 注意这种写法 实相当于是让p变短从而显得q变长 即出现多次的情况）

如果前一个位置和s不匹配，那没办法了，※的作用只可能是让前一个字符出现0次，所以这种情况就只有一种可能性

dp[i][j] = dp[i][j - 2] if(s[i - 1] != p[j - 1] && p[j - 1] != '.')

分析到这，这题的dp就结束了，确实是比较复杂，但实际想清楚了也就那么几种情况。下面是完整代码

代码

class Solution {
public:
    bool isMatch(string s, string p) {
        vector<vector<bool>> dp(s.size() + 1, vector<bool>(p.size() + 1, false));
        dp[0][0] = true;
 
        // s空 只有p为* 才可能为true
        // p空 s不空 显然都是false
        // p长度从2开始考虑 不从1的原因在于 s为空 p为一个字符的情况 是绝对匹配不了的 
        // 所以可以直接从2开始考虑
        for (int j = 2; j <= p.size(); ++j) {
            dp[0][j] = (p[j - 1] == '*') && dp[0][j - 2];
        }
        
        // p s都不为空
        for (int i = 1; i <= s.size(); ++i) {
            for (int j = 1; j <= p.size(); ++j) {
                if (s[i - 1] == p[j - 1] || (p[j - 1] == '.')) dp[i][j] = dp[i - 1][j - 1];
                // 这里j>=2实际是可以不要的 还是因为p的第一个字符不可能是* 但是为了看上去更准确就加上了
                else if(j >= 2 && p[j - 1] == '*') {
                    if (p[j - 2] != s[i - 1] && (p[j - 2] != '.')) dp[i][j] = dp[i][j - 2];
                                    // 0次 			  1次 				多次
                    else dp[i][j] = dp[i][j - 2] || dp[i][j - 1] || dp[i - 1][j];
                }
            }
        }
        return dp[s.size()][p.size()];
    }
};